【YOLO系列】 YOLOv4之BN、CBN、CmBN(附代码)

一、BN

        论文下载：Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift

1、背景

        在神经网络训练过程中，输入的数据可能具有分布不平衡、相关性强等问题，同时随着前一层参数的变化，每一层输入的分布也会发生变化，这使得训练深度神经网络变得非常复杂，可能会出现收敛速度慢、梯度消失或梯度爆炸等问题。

        论文中提出，虽然随机梯度下降（SGD）的方法简单有效，但它需要调整模型的超参数，特别是用于优化的学习率以及模型参数的初始值。训练时，因为每一层的输入都会受到前一层参数的影响，所有网络参数的微小变化会随着网络的加深而放大。而在训练过程中输入数据的分布发生变化时，导致每一层的输入分布也会发生变化的现象被称为内部协变量偏移现象，这种现象会使得网络的训练过程变得困难，因为每一层的参数都需要不断的适应新的输入数据分布。

2、内部协变量偏移（Internal Covariate Shift）到底是什么？

        （1）内部（Internal）指的是深层网络的隐含层，是在网络内部发生的事情，因此说明Covariate Shift不只发生在输入层；

        （2）协变量（covariate）在神经网络中是指输入数据的特征或变量，它们作为网络的输入，影响着神经网络的输出结果。在神经网络训练的过程中，协变量决定了输入数据的分布和特征。

        所以，内部协变量偏移说简单点就是在训练时由于网络参数的变化而导致隐含层的输入数据分布会不一样的现象。

3、那么，如何减少内部协变量偏移？

        针对这个现象，有学者发现如果输入被白化（whitened，常用在图像处理中），即通过线性变换为均值为0，方差为1，同时去相关，则网络训练收敛的更快。于是，作者就在思考，每一层（深度神经网络的英每一个隐含层都是可以看做输入层）的输出都会作为下一层的输入，那如果将每一个隐含层节点的激活输入分布都固定下来，这样是不是就可以避免“Internal Covariate Shift”问题？因此作者通过白化每一层的输入，实现输入的固定分布，证明了在每个训练对每一层的输入实现相同的白化是有利的，这也就是BN的来源。

        作者将批量归一化（Batch Normalization, BN）定义为通过固定层输入的均值和方差的归一化步骤来实现输入数据的固定。BN可以通过改善梯度流，减少梯度对参数尺度或其初始值的依赖，因此允许使用更高的学习率，并且不会有发散的风险。此外，BN使模型规范化，还可以减少对Dropout的需求。

        这就是我们为啥经常看到很多网络中都是conv+BN+激活函数的结构，因为这样可以有效的缓解了内部协变量偏移的现象。

4、均值为0，方差为1方法是什么归一化方法？

        将数值缩放到0附近，使得数据的分布均值为0，标准差为1的归一化被称为Zero-Score归一化，也就是使输入数据呈标准正态分布。

        其中，μ为原始特征的均值，σ为原始特征的标准差（方差）

5、BN的本质思想是什么？

        使用BN的原因其实就是因为深度神经网络在做非线性变换前的激活函数输入值（y=wx+b，x为输入值），随着网络深度的加深或者在训练过程中，其分布逐渐发生偏移或者变动，一般是整体分布逐渐往非线性函数（激活函数）的取值区间的上下限两端靠近（对于sigmod函数来说，它的输入值，即y是大的负值或正值），这样会导致反向传播时，低层神经网络的梯度消失，这就是训练深度神经网络收敛越来越慢的原因。

        而BN就是通过一定的归一化方法，把每层神经网络任意神经元的输入值的分布强行拉回到均值为0方差为1的标准正态分布，其实就把越来越偏的分布拉回来，这样使得激活函数的输入值落在激活函数比较敏感的区域，这样输入的小变化就会导致损失函数较大的变化，即让梯度变大，避免梯度消失问题产生，而且梯度变大意味着学习收敛速度快，能大大加快训练速度。

        总之一句话：对于每个隐含层的神经元，把逐渐向激活函数取值区间极限饱和区（大的负值或正值）靠近的输入分布强制拉回均值为0方差为1的标准正态分布，使得激活函数的输入值落在比较敏感的区域，以此避免梯度消失或爆炸的问题。这也解释了为啥BN通常在激活函数之前的原因。

6、图解一下为什么要进行BN

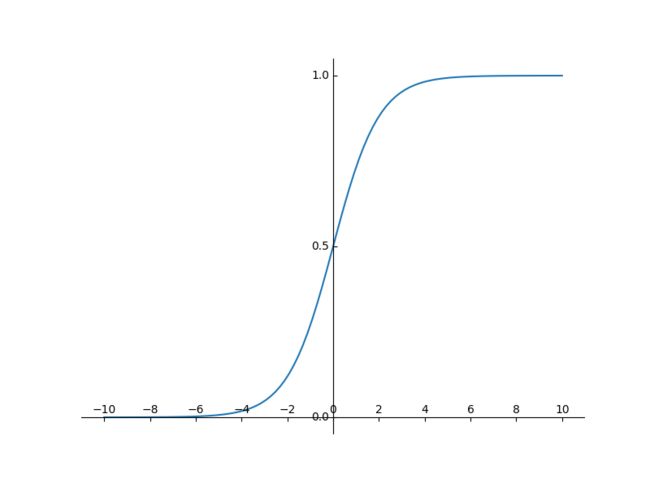
        均值为0，方差为1的标准正态分布如下图所示：

        从上图可以知道，通过归一化变换后的激活函数输入值落在[-1, 1]的概率为64%，落在[-2, 2]之间的概率为95%。也就是说y=wx+b，x为初始输入值，y为激活函数输入值，假如激活函数为sigmod，那么通过sigmod输出的值是多少呢，请看下图。

        也就是说，当sigmod函数的输入在[-2, 2]之间（称之为线性区）时，sigmod输出值在[0.12, 0.88]之间，而sigmod函数的导数为G' = sigmod* (1-sigmod)，其取值区间为[0, 0.25]，具体如下图所示。因此通过BN后的数据，落在了激活函数的非敏感区域，也有效避免了梯度消失的现象。

        如下图所示，当均值不同时，归一化后的取值范围是向左或者向右平移，而方差的改变只是影响正态分布峰值的变化和曲线的平缓程度。

        因此假设原来的输入数据没有经过BN（均值为0，方差为1）的均值为-5， 方差为0.5， 那么意味着95%的都会落在[-7, -3]之间，那么对应的sigmod函数值就明显趋于0， 这是典型的梯度饱和区间，在这个区域的梯度变化很慢（结合导函数图），而且梯度很小甚至会消失

7、BN实现

        （1）数据处理

        对于隐含层内的每个神经元的激活值（输入值）来说，进行如下变换：

        （2）scale和shift操作

        前面说过经过这个变换后某个神经元的激活值形成了均值为0，方差为1的正态分布，目的是把值往要进行的非线性变换（激活函数）的线性区拉动，增大导数值，增强反向传播信息的流动性，加快训练收敛速度。

        但是简单的归一化隐含层的每个输入可能会改变网络的表达能力，因为如果每个隐含层都通过 BN，就相当于把非线性函数替换成了线性函数，这意味这深度的意义就没有了，即如果多层都是相同的线性变换的话，其实多层线性网络就跟一层线性网络是等价的，这就意味着网络的表达能力下降了。

        因此作者在文中提出两个参数：scale、shift，这两个参数是通过训练学习得到的，意思是通过scale和shift将变换后的符合标准正态分布的值左移或右移一点同时胖一点或瘦一点，每个值的移动程度不一样，这样等价与非线性函数的值从正中心的线性区往非线性区移动了一下。

        其实核心思想就是在非线性区和线性区找到一个平衡点，这样变换后的数据既可以有非线性的较强的表达能力，又可以避免太靠近非线性区而使得网络收敛太慢的现象。具体表达式如下：

        （3）具体流程

        BN的具体操作流程如下图所示

def BN(feature, mean, var):
    feature_shape = feature.shape  # (2, 2, 2, 2) = (batch_size, C, H, W)
    for i in range(feature_shape[1]):  # feature_shape[1] = 2 = C: channel
        # [batch, channel, height, width]
        feature_t = feature[:, i, :, :]
        mean_t = feature_t.mean()  # 求出整个channel的mean
        # 训练：总体标准差
        std_t1 = feature_t.std()  # 求出整个channel的std
        # 测试：样本标准差
        std_t2 = feature_t.std(ddof=1)

        # bn   对第i个channel的每一个元素  进行norm  初始伽马=1 贝塔=0
        feature[:, i, :, :] = (feature[:, i, :, :] - mean_t) / std_t1

        # update calculating mean and var  记录下mean和var用于测试集用
        # 训练时使用总体标准差   测试时使用样本标准差
        # 0.1为momentum
        mean[i] = mean[i] * (1 - 0.1) + mean_t * 0.1
        var[i] = var[i] * (1 - 0.1) + (std_t2 ** 2) * 0.1

    return feature, mean, var

8、BN的优缺点

        （1）优点

        a. 加速神经网络的训练速度，使网络更快地收敛；

        b. 减少网络对初始参数的依赖，增加网络的稳定性；

        c. 抑制过拟合，提高模型的泛化能力；

        d. 允许使用更高的学习率，加快模型训练。

        （2）缺点

        a. BN的引入增加了模型的计算量和内存占用；

        b. BN对批次大小比较敏感，小批次大小可能导致估计的均值和方差不准确；

        c. BN在小数据集上的效果可能有限。

二、CBN

        论文下载：Cross-Iteration Batch Normalization

1、背景

        上面讲到BN对批次大小比较敏感，即在小批量的情况下BN的效果会显著降低。当一个批次中包含很少的样本时，在训练迭代期间，就无法可靠地估计这个批量的均值和方差。

        针对这个问题，清华和微软的学者提出了一种交叉迭代批处理归一化（CBN）的方法，利用多个最近迭代的样本的来提高数据估计的质量，同时在迭代过程中由于网络权重的变化，作者提出了基于泰勒多项式的技术来补偿网络权重的变化，从而准确的估计统计量并进行有效的归一化。

2、什么是CBN

        在文中，作者针对BN在小批量的问题，利用多个最近迭代的样本的来提高数据估计的质量，但是由于在迭代过程中网络权重不断变化，来自不同迭代的网络激活不能相互比较，因此作者提出一种基于泰勒多项式的技术来补偿迭代之间网络权值变化，从而有效利用之前迭代的样本来改进批量归一化，这种方法就是交叉迭代的批量归一化（CBN）。

        说简单点，CBN就是一种通过补偿迭代之间网络权值的变化而有效的利用之前的迭代样本来改进批量归一化的方法。

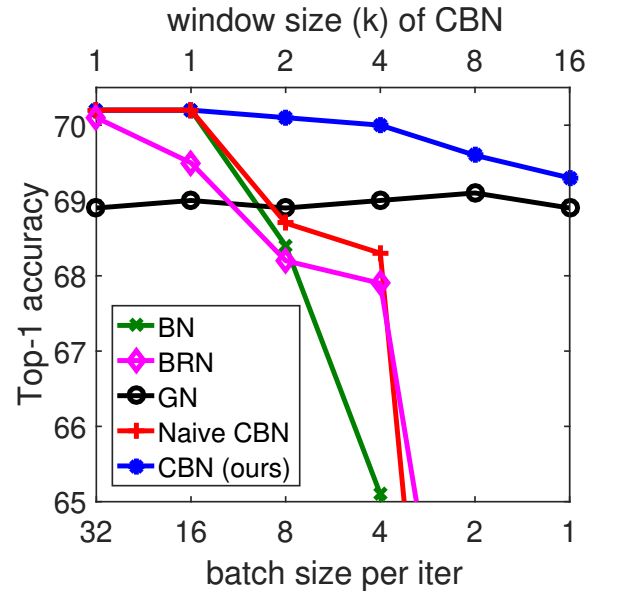
        作者将BN、BRN、GN、Naive CBN、CBN在不同批次数量下的精度进行了对比，CBN在不同的批处理规模上表现出相对稳定的性能。

3、CBN是怎么工作的

        （1）Leveraging Statistics from Previous Iterations

        第次迭代的统计和是在网络权值下计算的,这使得它们在当前迭代中已过时。因此，直接聚合来自多个迭代的统计信息会产生对平均值和方差的准确估计，从而导致显著的性能下降。

        作者观察到，由于梯度训练的性质，网络权值在连续迭代之间平稳变化。这就允许用过泰勒多项式，从现在的和去近似和。

        为网络权重的梯度统计，代表泰勒多项式的二阶高阶项，非常小，可以忽略。

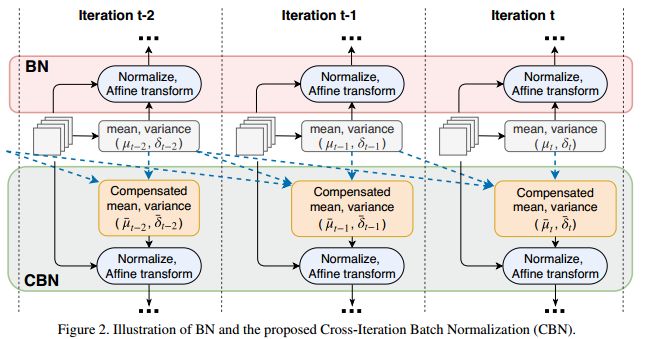
        （2）Cross-Iteration Batch Normalization

        CBN的工作方式如上图所示：将最近k-1次迭代的统计量与当前迭代t统计量相加，得到CBN中的使用统计量，然后在计算出当前层的BN参数，计算方式如下

        这里需要注意的是，在有效统计时>上述式子是一直都会满足，但是利用泰勒展开估算就不一定能满足条件，所以上述式中使用了max函数来保证这一点。

        最后，CBN的更新方式与BN一样，但是对于CBN，用于计算当前迭代统计量的有效样本数是原始BN的k倍。

4、CBN优缺点

        （1）优点

        a. 提高了BN的稳定性，CBN通过累积统计信息来减少批次内样本数量的影响，从而提高了归一化的准确性和稳定性；

        b. 加速训练收敛：由于CBN利用了之前迭代的统计信息，可以更快地收敛到较好的模型；

        c. 减少了对大批量训练的依赖：传统BN在小批量下训练时可能不稳定，需要较大的批量大小才能获得较好的效果。而CBN通过使用最近的迭代信息，可以在小批量训练时获得更好的性能。

        （2）缺点

        a. 内存占用较大：由于每个迭代需要计算数据、偏导数等，所以会导致计算开销和内存占用增加；

        b. 训练速度较慢：由于每个迭代都需要累积统计最近的信息和进行归一化，所有CBN的训练速度相对较慢。

5、CBN代码

        CBN的伪代码如下：

import torch.nn as nn
import torch


class CBatchNorm2d(nn.Module):
    def __init__(self, num_features, eps=1e-5, momentum=0.1, affine=True,
                 track_running_stats=True,
                 buffer_num=0, rho=1.0,
                 burnin=0, two_stage=True,
                 FROZEN=False, out_p=False):
        super(CBatchNorm2d, self).__init__()
        self.num_features = num_features
        self.eps = eps
        self.momentum = momentum
        self.affine = affine
        self.track_running_stats = track_running_stats

        self.buffer_num = buffer_num
        self.max_buffer_num = buffer_num
        self.rho = rho
        self.burnin = burnin
        self.two_stage = two_stage
        self.FROZEN = FROZEN
        self.out_p = out_p

        self.iter_count = 0
        self.pre_mu = []
        self.pre_meanx2 = []  # mean(x^2)
        self.pre_dmudw = []
        self.pre_dmeanx2dw = []
        self.pre_weight = []
        self.ones = torch.ones(self.num_features)

        if self.affine:
            self.weight = Parameter(torch.Tensor(num_features))
            self.bias = Parameter(torch.Tensor(num_features))
        else:
            self.register_parameter('weight', None)
            self.register_parameter('bias', None)
        if self.track_running_stats:
            self.register_buffer('running_mean', torch.zeros(num_features))
            self.register_buffer('running_var', torch.ones(num_features))
        else:
            self.register_parameter('running_mean', None)
            self.register_parameter('running_var', None)
        self.reset_parameters()

    def reset_parameters(self):
        if self.track_running_stats:
            self.running_mean.zero_()
            self.running_var.fill_(1)
        if self.affine:
            self.weight.data.uniform_()
            self.bias.data.zero_()

    def _check_input_dim(self, input):
        if input.dim() != 4:
            raise ValueError('expected 4D input (got {}D input)'
                             .format(input.dim()))

    def _update_buffer_num(self):
        if self.two_stage:
            if self.iter_count > self.burnin:
                self.buffer_num = self.max_buffer_num
            else:
                self.buffer_num = 0
        else:
            self.buffer_num = int(self.max_buffer_num * min(self.iter_count / self.burnin, 1.0))

    def forward(self, input, weight):
        # deal with wight and grad of self.pre_dxdw!
        self._check_input_dim(input)
        y = input.transpose(0, 1)
        return_shape = y.shape
        y = y.contiguous().view(input.size(1), -1)

        # burnin
        if self.training and self.burnin > 0:
            self.iter_count += 1
            self._update_buffer_num()

        if self.buffer_num > 0 and self.training and input.requires_grad:  # some layers are frozen!
            # cal current batch mu and sigma
            cur_mu = y.mean(dim=1)
            cur_meanx2 = torch.pow(y, 2).mean(dim=1)
            cur_sigma2 = y.var(dim=1)
            # cal dmu/dw dsigma2/dw
            dmudw = torch.autograd.grad(cur_mu, weight, self.ones, retain_graph=True)[0]
            dmeanx2dw = torch.autograd.grad(cur_meanx2, weight, self.ones, retain_graph=True)[0]
            # update cur_mu and cur_sigma2 with pres
            mu_all = torch.stack(
                [cur_mu, ] + [tmp_mu + (self.rho * tmp_d * (weight.data - tmp_w)).sum(1).sum(1).sum(1) for
                              tmp_mu, tmp_d, tmp_w in zip(self.pre_mu, self.pre_dmudw, self.pre_weight)])
            meanx2_all = torch.stack(
                [cur_meanx2, ] + [tmp_meanx2 + (self.rho * tmp_d * (weight.data - tmp_w)).sum(1).sum(1).sum(1) for
                                  tmp_meanx2, tmp_d, tmp_w in
                                  zip(self.pre_meanx2, self.pre_dmeanx2dw, self.pre_weight)])
            sigma2_all = meanx2_all - torch.pow(mu_all, 2)

            # with considering count
            re_mu_all = mu_all.clone()
            re_meanx2_all = meanx2_all.clone()
            re_mu_all[sigma2_all < 0] = 0
            re_meanx2_all[sigma2_all < 0] = 0
            count = (sigma2_all >= 0).sum(dim=0).float()
            mu = re_mu_all.sum(dim=0) / count
            sigma2 = re_meanx2_all.sum(dim=0) / count - torch.pow(mu, 2)

            self.pre_mu = [cur_mu.detach(), ] + self.pre_mu[:(self.buffer_num - 1)]
            self.pre_meanx2 = [cur_meanx2.detach(), ] + self.pre_meanx2[:(self.buffer_num - 1)]
            self.pre_dmudw = [dmudw.detach(), ] + self.pre_dmudw[:(self.buffer_num - 1)]
            self.pre_dmeanx2dw = [dmeanx2dw.detach(), ] + self.pre_dmeanx2dw[:(self.buffer_num - 1)]

            tmp_weight = torch.zeros_like(weight.data)
            tmp_weight.copy_(weight.data)
            self.pre_weight = [tmp_weight.detach(), ] + self.pre_weight[:(self.buffer_num - 1)]

        else:
            x = y
            mu = x.mean(dim=1)
            cur_mu = mu
            sigma2 = x.var(dim=1)
            cur_sigma2 = sigma2

        if not self.training or self.FROZEN:
            y = y - self.running_mean.view(-1, 1)
            # TODO: outside **0.5?
            if self.out_p:
                y = y / (self.running_var.view(-1, 1) + self.eps) ** .5
            else:
                y = y / (self.running_var.view(-1, 1) ** .5 + self.eps)

        else:
            if self.track_running_stats is True:
                with torch.no_grad():
                    self.running_mean = (1 - self.momentum) * self.running_mean + self.momentum * cur_mu
                    self.running_var = (1 - self.momentum) * self.running_var + self.momentum * cur_sigma2
            y = y - mu.view(-1, 1)
            # TODO: outside **0.5?
            if self.out_p:
                y = y / (sigma2.view(-1, 1) + self.eps) ** .5
            else:
                y = y / (sigma2.view(-1, 1) ** .5 + self.eps)

        y = self.weight.view(-1, 1) * y + self.bias.view(-1, 1)
        return y.view(return_shape).transpose(0, 1)

    def extra_repr(self):
        return '{num_features}, eps={eps}, momentum={momentum}, affine={affine}, ' \
               'buffer={max_buffer_num}, burnin={burnin}, ' \
               'track_running_stats={track_running_stats}'.format(**self.__dict__)

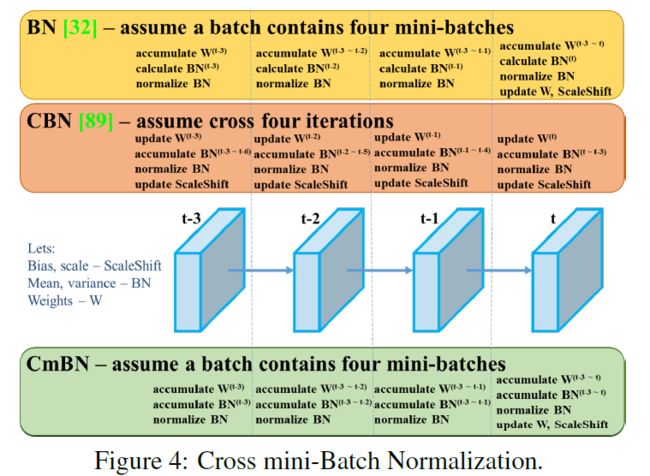
三、CmBN

        CmBN（Cross mini-Batch Normalization）是CBN的修改版。CBN主要用来解决在Batch-Size较小时，BN的效果不佳问题。CBN连续利用多个迭代的数据来变相扩大Batch-Size从而改进模型的效果（每次迭代时计算包括本次迭代的三个迭代后统一计算整体BN）。而CmBN是独立利用多个mini-batch内的数据进行BN操作。（每四个迭代后统一计算一次整体BN）