GNN框架优化GNNAdvisor: An Adaptive and Efficient Runtime System for GNN Acceleration on GPUs

OSDI’21

Abstract

GNNAdvisor

• 从GNN模型和输入图中寻找与性能相关的特征，作为优化点
• 实现为GNN计算定制的2D工作负载管理，提升GPU利用率和性能
• 利用GPU内存结构，根据GPU内存结构和GNN工作负载的特点协调GNN的执行
• 为了实现自动优化，继承了一个轻量级的分析模型进行参数搜索

1. Introduction

目前，支持GNN训练和推理的工作可以分为两类：

• 图处理系统，融合神经操作
• 神经网络框架，扩展支持基于向量的图操作

但都是初步的、不完善的，有三个方面的缺陷：

• 没有利用GNN的输入信息：GNN模型有不同的层序列、聚合函数的类型、特征向量的维度，输入的图数据也有不同特征。现在的GNN框架（pyg, neugraph, dgl），采用的是一刀切的优化模式，无法最大化优化特定GNN应用
• 没有针对GNN的优化：更新阶段的NN操作是密集的、访存规律的，但聚合阶段的图操作是稀疏的、访存不规律的。当前的GNN框架的图操作来自图处理系统，针对的是标量属性，而GNN中每个节点都有一个embedding，因此应在embedding上积极利用并行。
• 对于不同输入，缺乏适应性的运行时支持：之前的GNN框架依赖python编程接口，使用编译器进行静态优化，但是GNN的一些特征在运行时才会显现出来（比如向量大小、节点度数），因此需要运行时优化。

提出GNNAdvisor

GNNAdvisor使用Pytorch作为前端，在底层是用CUDA写的，并用pytorch wrapper集成到pytorch里面。它可以被看作是具有kernel优化、运行时支持的operator

使用GNNAdvisor实现的两层GCN如下：

import GNNAdvisor as GNNA
import torch

# create a GCN class
class GCN(torch.nn.Module):
    def __init__(self, inDim, hiDim, outDim, nLayers):
        self.layers = torch.nn.ModuleList()
        self.layers.append(GNNA.GCNConv(inDim, 	hiDim))
        for i in range(nLayers - 2):
            layer = GNNA.GCNConv(hiDim, hiDim)
            self.layers.append(layer)
        self.layers.append(GNNA.GCNConv(hiDim, outDim))
        self.softmax = torch.nn.Softmax()
    
    def forward(self, X, graph, param):
        for i in range(len(self.layers)):
            X = self.layers[i](X, graph, param)
            X = self.ReLU(X)
        X = self.softmax(X)
        return X

# define a 2-layer GCN model
model = GCN(inDim=100, hiDim=16, outDim=10, nLayers=2)

# loading graph and extracting input properties
graphObj, inputInfo = GNNA.LoaderExtractor(graphFile, model)

# set runtime parameters automatically
X, 	graph, param = GNNA.Decider(graphObj, inputInfo)

# run model
predict_y = model(X, graph, param)

# compute loss and accuracy
# gradient backpropagation for training

贡献：

• 第一个提出了分析输入（模型、图数据）的特征
• 提出了具有参数的针对GNN的系统优化：2D工作负载管理、针对GNN的内存优化。并结合分析建模和参数自动选择，去简化搜索空间
• DGL 3.02X NeuGraph 4.36X

2. Background and Related Work

2.1 Graph Neural Network

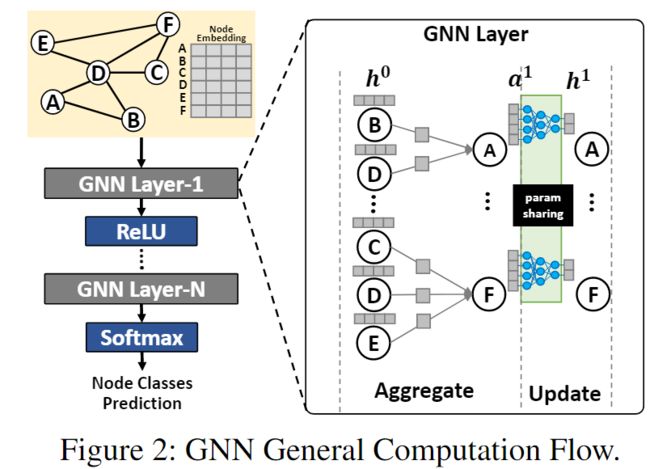
GNN计算节点v在第k+1层的embedding的公式如下：
$$\begin{gathered} a_v^{k+1}=Aggregat{e}^{(k+1)}(h_u^k|u\in N(v)\cup h_v^k) \\ {h}_v^{k+1}=Updat{e}^{(k+1)}(a_v^{k+1}) \end{gathered}$$
其中，$a_v^{k+1}$表示聚合了邻居信息（比如邻居的embedding）之后的结果，$h_u^k$表示节点u在第k层的embedding，$N(v)$表示节点v的邻居节点

Aggregate: 图操作，聚合邻居的信息（比如邻居节点的embedding）

Update: NN操作，比如全连接层、MLP，将aggregate得到的结果：乘w、加b（w和b都是可学习的参数）

经过多次Aggregate和Update迭代之后（也就是多个GNN层之后），得到输出embedding，可以用来执行下游任务（比如节点分类、链接预测等）

注意：初始的embedding，可以是从图数据中得到的、也可以是通过embedding生成算法得到的，并不包含在GNN的执行过程中

2.2 Graph Processing Systems

有三点原因，不以传统的图处理系统为基础，拓展GNNAdvisor的工作：

• 图处理系统的图算法优化不适合GNN
• 图处理系统没有考虑GNN的embedding并行（传统的图处理系统一般是节点并行，而GNN的每个节点都有维度很大的embedding，这又是一个并行）
• 图处理系统没有NN操作

2.3 Deep Learning Frameworks

Pytorch、TensorFlow，内置了许多NN operator，针对欧几里得数据做了很多优化，但是对于图这样的非欧几里得数据，面临一些挑战：

• PyG、DGL关注多模型上的编程性、通用性，但是缺乏后端支持来实现高性能。比如：PyG使用CUDA实现的torch-scatter库作为自己的图聚合操作的主要构成部分，但是torch-scatter在处理大规模稀疏图和高维节点embedding时性能不佳，问题在于其kernel采用了高开销的原子操作来执行节点embedding传播，这种方法借鉴了图处理系统的设计原则，但在面临大规模稀疏图与高维节点embedding时性能不佳；DGL采用现成的SPMM（比如cuSparse库的csrmm2）来进行sum-reduced aggregation，同时利用自己的cuda kernel处理带有边属性的聚合。
• PyG、DGL的kernel是硬编码的，无法根据输入图数据的特性、模型的特性、GPU硬件的特性等进行自适应的改变。（用户无法自己改变）

3. Input Analysis of GNN Applications

3.1 GNN Model Information

GNN的update较为固定，但是aggregation变化较多，主流的aggregation方法有两种：

• 只聚合邻居节点的embedding（比如GCN）。实践中，一般先更新降低embedding的维度（embedding矩阵和权重矩阵相乘），然后再聚合，以降低聚合时的数据移动。此时，提升内存局部性很有利（比如将embedding放到快速内存，如GPU的L1 cache）
• 聚合时，涉及到边的特征，需要将边的权重应用到邻居节点上（比如GIN）。此时，不能先执行更新以降维了，因为聚合时需要完整的embedding来计算边的特征。只能先聚合再更新。此时，内存局部性不好利用，因为快速内存可能无法满足完整的embedding的内存需求。但是，可以利用并行计算，比如沿着embedding的维度划分工作负载，利用多个并发线程执行并行计算。

举例来说，输入embedding维度是128，隐藏维度是16。GCN先更新，embedding维度从128降到16，然后以16的embedding维度进行聚合；GIN先以128的embedding维度进行聚合，再更新。因此对于GCN来说，更倾向于内存优化（把embedding放到cache里面）；对于GIN来说，更倾向于并行计算上的优化（将较大的embedding维度进行划分）

3.2 Graph Information

Node Degree & Embedding Dimensionality

现实世界的图的节点度数大多遵循幂律分布，这会带来负载不均衡的问题（如果划分节点的话），在GNN上，负载不均衡的问题更严重（相对传统的图处理系统来说，他们的节点带的是标量），因为每个节点都带有一个更高维度的embedding。

节点embedding使得某些传统图处理系统上的cache优化失效，因为embedding维度更高，而cache的内存相对较小，存不下太多embedding。比如，对于节点带有标量属性的传统图处理系统，64KB的L1 cache可以存放$16\times 10^3$个node，而对于embedding维度为64的GNN来说，只能存放$256$个node。

根据节点度数和embedding维度，可以估计节点的负载。如果负载取决于节点度数，那么从节点的邻居上并行，同时执行更多的邻居；如果负载取决于embedding维度，那么从embedding的维度上并行。

Graph Community

图社区是现实世界图的一个关键特征，一小小组节点，组内保持强连接（即很多边连接），组间保持弱连接（即较少的边连接）。

图处理系统以节点为中心的聚合方式中，每个节点独立地load自己的邻居节点（每个节点带有标量属性）（如Fig. 3(b)），会重复加载，但是由于是并行load，因此并行带来的优势与重复加载引入的冗余相抵消。但对于GNN来说，每个节点都带有高维的embedding，此时，重复加载带来的额外成本显著提高。若采用图社区的特点，则可减少冗余加载（如Fig. 3©）。

4. 2D Workload Management

GNNAdvisor包含了由输入驱动的带参数的2D Workload Management，包含三种技术：coarse-grained neighbor partitioning, fine-grained dimension partitioning, warp-based thread alignment

4.1 Coarse-grained Neighbor Partitioning

将邻居节点划分为大小相等的neighbor group（NG），并将NG作为调度的基本单元。

如Fig. 4所示，NG的大小取为2（这是一个可调的参数），节点0有四个邻居2 3 6 10，划分到NG-0和NG-1中，注意：一个NG中只放同一节点的邻居（便于调度、同步），当邻居节点的数量不能被NG的大小整除时，会带来不平衡，可以通过改变NG的大小来缓解。

为了支持neighbor group，引入neighbor-partitioning module和neighbor-partitioning graph store，neighbor-partitioning建立在graph loader上，将图上的邻居节点划分为一个个NG；neighbor-partitioning graph store存储关于分组的元信息，包括分组id、源节点、邻居节点的起始位置。

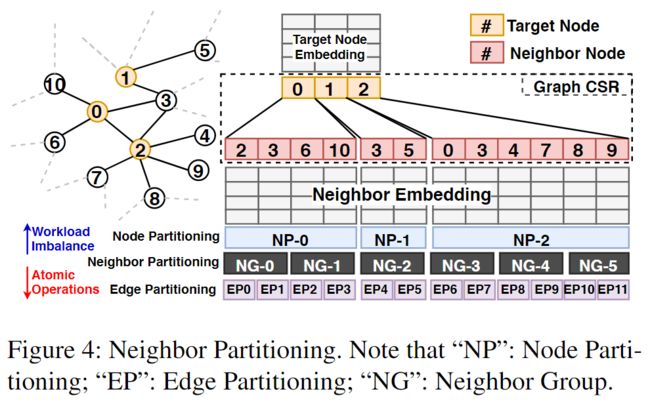
划分邻居进行聚合有三个好处：

• 和粒度更粗的以节点为中心的划分相比，减小了负载不均衡
• 和粒度更细的以边为中心的划分（比如PyG）相比，避免了管理许多小型单元带来的调度、同步开销
• 引入了一个与性能相关的的参数：neighbor-group size(ngs)，可以用来设计参数、性能调优

划分邻居，可以缓解低维embedding的负载不均衡问题，对于高维embedding，还需要进一步的操作：Fine-grained Dimension Partitioning

4.2 Fine-grained Dimension Partitioning

沿embedding划分一个NG的负载，如Fig. 5所示，原始的NG的负载被分配给了11个连续的线程，每个线程负责embedding的一个维度的聚合（如果ngs=2，那么一个线程管理两个embedding的一个维度上的聚合），如果维数大于线程数，就迭代。

使用维度划分有两个原因：

• 可以处理更大范围的embedding大小，可以增加线程的数量、或进行多次迭代，来应对维度变化
• 引入了另一个与性能相关的参数：dimension-worker(dw)，工作线程的数量，这个值可以帮助平衡线程级并行和每个线程的计算负载

4.3 Warp-based Thread Alignment

4.1、4.2在逻辑上描述了如何平衡负载，但是没有回答如何将负载映射到GPU硬件的层面上。

一种直观的想法是：将连续的线程分配给不同的ng（一个warp对应多个ng），同时处理多个ng（如Fig. 6(a)），但是不同的线程可能具有不同的行为（计算、访存），而warp内部是SIMT，因此，会有部分线程处于等待状态，导致线程发散。（如Fig. 6(a)）

因此，让一个warp管理一个ng。可以很好的并行化，减少线程发散。（如Fig. 6(b)）

有三个好处：

• 最小化线程间的同步（比如原子操作），减少访存冲突。（**个人理解：**Fig. 6(a)这样的方法，一个warp管理三个ng，三个ng可能包含了相同的节点，因此warp内的不同线程可能会访问同一块内存，此时会导致同步操作或原子操作。而Fig. 6(b)这样的方法，就没有这一问题，因为每个线程都是访问不同的数据，不会冲突）
• 分配的warp数量更多了，可以提高整体并行性、提高SM利用率、隐藏访存延迟。（**个人理解：**每个warp都要访问全局内存，在访存的时候，warp scheduler切换到别的warp执行计算，以隐藏访存延迟，warp数量越多，隐藏延迟的机会越多）
• 合并内存访问。（**个人理解：**现在是连续的线程访问连续的内存空间（同一embedding的不同位置），是合并的。而Fig. 6(a)这种方法，连续的线程，访问来自三个ng的embedding，不是连续的内存空间，因此不是合并的内存访问）

5. Specialized Memory Optimization

为了进一步利用2D负载，引入了针对GNN的内存优化，Community-aware Node Renumbering和Warp-aware Memory Customization

5.1 Community-aware Node Renumbering

为了利用图社区的性质，引入lightweight node renumbering，重排节点id，以提高GNN聚合时的时空局部性。由代码可知：重排是在load之后进行的。

idea：将节点id的邻近性映射到GPU计算单元上。在GNNAdvisor中，2D workload management将节点id连续的节点的邻居分组分配给连续的warp（如果两个节点的id是连续的，那么它们的邻居分组会被分配给连续的warp）。因此，它们更有可能被分配到同一个SM上，来提高加载的共同邻居的数据局部性。

When to apply ? （不是什么时间使用，而是在什么时候，也就是针对什么图使用）

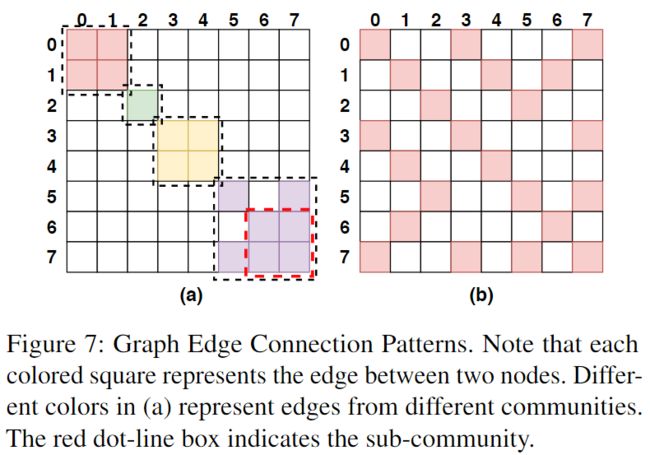
首先要回答一个问题，什么样的图更能从node renumbering中获利，作者的答案是，如Fig. 7(a)这样的、邻接矩阵近似对角模式的图，很难获利，因为这样的图的社区内部的节点id已经是连续的了；而像Fig. 7(b)这样的、形状很不规则的图，更容易从node renumbering中获利。因此提出一个metric—***Averaged Edge Span(AES)***来决定执行重排是否是有利的。

其中，E是图的边集，#E是边数，$sr{c}_{id}$和$tr{g}_{id}$是每条边源节点、目标节点的id。在加载图的时候，计算AES，作者在大型图上的分析表明：当$\sqrt{AES}>\lfloor \frac{\sqrt{N}}{100}\rfloor$时，更有可能提升性能（注意，N前面有个#，typora公式内部不让打#，所以没打上去）

How to apply ?

利用了Rabbit Reordering，这是一种完全并行且成本低廉的图重排序技术。具体而言，它首先通过分层合并边和聚类节点来最大化图的模块化程度。然后通过深度优先搜索（DFS）遍历为每个聚类生成节点顺序。

更重要的是，Rabbit Reordering可以层次化地捕获图社区（即，一组较小的子社区包含在一个更大的社区中，如Fig. 7(a)所示）。不同粒度的这些社区可以很好地匹配GPU缓存层次结构，较小的子社区（占用一个 SM）可以从L1缓存中获得数据局部性的好处，而较大的社区（占用多个 SM）则可以从更大的L2缓存中获得数据局部性。

5.2 Warp-aware Memory Customization

PyG、Gunrock在读写embedding和聚合时，使用了大量的全局内存访问和原子操作，带来了巨大的开销，并未充分利用shared memory。

作者提出了一种以warp为中心的共享内存优化技术。

为每个邻居组（warp）的目标节点保留一个共享内存空间（每个目标节点对应一块空间），这样来自warp的线程可以将规约的中间结果缓存到共享内存中。随后，在线程块内部，我们仅为每个目标节点指定一个warp（称为leader），以将中间结果从共享内存复制到全局内存。具体而言，每个warp（维护在warpPtr中）有三个属性：nodeSharedAddr（邻居分组聚合结果的共享内存地址）、nodeID（目标节点的ID）和leader（一个布尔标志，指示当前warp是否是用于将结果从共享内存更新到全局内存的leader warp）。

6. Design Optimization

GNNAdvisor的Decider中的分析模型和自动参数选择功能。

Analytical Modeling

GNNAdvisor的性能分析模型有两个变量：WPT是workload per thread，SMEM是shared memory usage per block

其中，ngs是一个邻居分组中的节点数量，Dim是embedding的维度，dw是4.2中负责聚合的线程数，tpb是thread per block，tpw是thread per warp，FloatS在GPU上是4字节。tpb是用户自己选择的，tpw在GPU上是32。

Parameter Auto Selection

为了确定ngs和dw的值，作者设计了以下两个步骤：

• 根据tpw和Dim决定dw的值，如果Dim >= tpw，dw = tpw；如果Dim < tpw，dw = tpw / 2。
• 根据dw和用户自己选择的tpb的值，来决定ngs的值。约束条件包括使WPT约等于1024，以及SMEM ≤ SMEMperBlock（现代 GPU 上的 SMEMperBlock 为48KB到96KB）。在不同的 GPU 上，即使CUDA核心数量和全局内存带宽不同，单线程的工作负载容量（由 WPT 衡量）保持相似。tpb通常选择为2的幂，但小于或等于1024。我们基于微基准测试和先前的文献的见解显示，较小的块（1到4个warp，即32 ≤ tpb ≤ 128）可以提高warp调度的灵活性，避免尾部效应，从而提高GPU的占用率和吞吐量。（知道了WPT、Dim、dw，根据上面的公式，可以求出ngs）

7. Evaluation

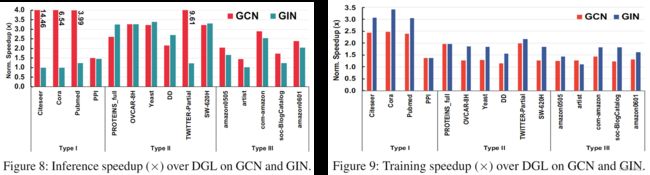
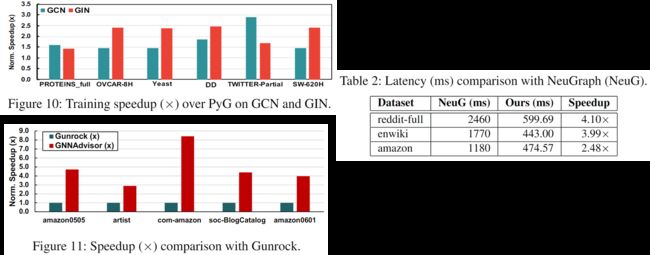
注意：DGL是最优秀的baseline，因此，选择在所有数据集上与DGL相比。而只在PyG、NeuGraph、Gunrock擅长的数据集上对比，其中Gunrock没法做GNN，因此使用SpMM来比较。

我的总结

这篇论文主要关注点在于如何利用model dataset的特点，来针对性地做优化，发挥在给定model dataset上的最大性能。

第三章，讲述了作者设计第四章、第五章优化策略所根据的性质。

第四章，考虑的主要是节点度数和embedding维度，对于节点度数大的而言，节点上的并行（邻居划分 4.1）更有帮助，而对于embedding维度大的而言，embedding上的并行（维度划分 4.2）更有帮助。4.3讲了如何在硬件层面上实现4.1 4.2提到的策略。

第五章，考虑的主要是图社区这一性质，将图数据经过节点重排（5.1）组织成图社区性质较强的形式，可以减少聚合阶段的重复load。5.2设计了一个算法来利用shared memory缓存归约的中间结果。

第六章，是如何自动选择第四章第五章的策略中涉及到的调优参数（ngs dw）。