表达式求值问题数据结构课程设计
完整代码在最后~~
1 需求分析
1.1 问题描述
表达式求值是程序设计语言编译中的一个最基本问题,就是将一个表达式转化为逆波兰表达式并求值。具体要求是以字符序列的形式从终端输入语法正确的、不含变量的整数表达式,并利用给定的优先关系实现对算术四则混合表达式的求值,并演示在求值过程中运算符栈、操作数栈、输入字符和主要操作变化过程。
要把一个表达式翻译成正确求值的一个机器指令序列,或者直接对表达式求值,首先要能正确解释表达式。任何一个表达式都是由操作符(operand)、运算符(operator)和界限符(delimiter)组成,我们成它们为单词。一般的,操作数既可以是常数,也可以是被说明为变量或常量的标识符;运算符可以分为算术运算符、关系运算符和逻辑运算符3类;基本界限符有左右括号和表达式结束符等。为了叙述的简洁,我们仅仅讨论简单算术表达式的求值问题。这种表达式只包括加、减、乘、除4种运算符。
人们在书写表达式时通常采用的是“中缀”表达形式,也就是将运算符放在两个操作数中间,用这种“中缀”形式表示的表达式称为中缀表达式。但是,这种表达式表示形式对计算机处理来说是不大合适的。对于表达式的表示还有另一种形式,称之为“后缀表达式”,即将运算符紧跟在两个操作数的后面。这种表达式比较适合计算机的处理方式,因此要用计算机来处理、计算表达式的问题,首先要将中缀表达式转化成后缀表达式,又成为逆波兰表达式。
1.2 问题要求
要求设计并编写一程序,选择适当的数据结构,解决上述问题,要求:
(1)输入输出界面友好;
(2)程序可读性强;
(3)程序具有较强的健壮性;
(4)读入原表达式并创建对应二叉树
(5)对二叉树进行前序遍历、中序遍历、后序遍历(非递归)
(6)输出逆波兰表达式
(7)正确输出最终表达式运算的结果
1.3 设计思路
为了实现表达式求值,可以首先读入原表达式(包括括号)并创建对应二叉树,其次对二叉树进行前序遍历、中序遍历、后续遍历(非递归),并输出逆波兰表达式,最后求解原表达式的值,同时对非法表达式格式能予以判断。
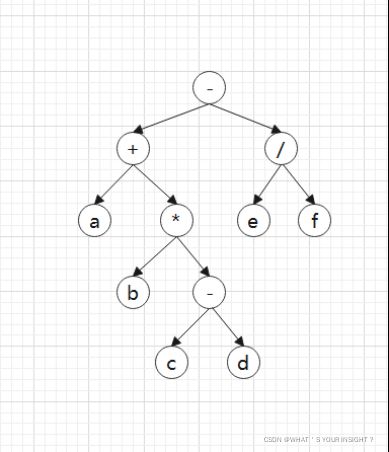
假设输入的表达式为ch=1+2*(3-2)-2/1;Tree是一个储存树根节点的栈,再用一个栈Optr存储operand(操作符),遇到数字就创建以该数字为根的树,并且它的左孩子和右孩子都置为空,然后放到Tree栈中。遇到operaor则将其与栈顶元素比较优先级,决定是否送到输出串中,这样处理之后能得到一个后续的排列,再建立二叉树,当遇到ab+这样的建立左右接点为a和b的根为+的树并返回根接点,当遇到操作符前面只有一个操作数的如c*这样的情况就建立右子接点为c的根接点为*的,左结点为上次操作返回的子树的根接点(这种情况下就是合并树的情况)。
非递归方法进行树的遍历需要用到栈结构。首先需要建立一个空栈(栈元素的类型是指向树结点的指针)。
首先将根节点压入栈中。然后进入循环。
如果栈不空,
弹出栈顶元素,
进行访问,
压入右子树(节点指针),
压入左子树(节点指针),
循环。
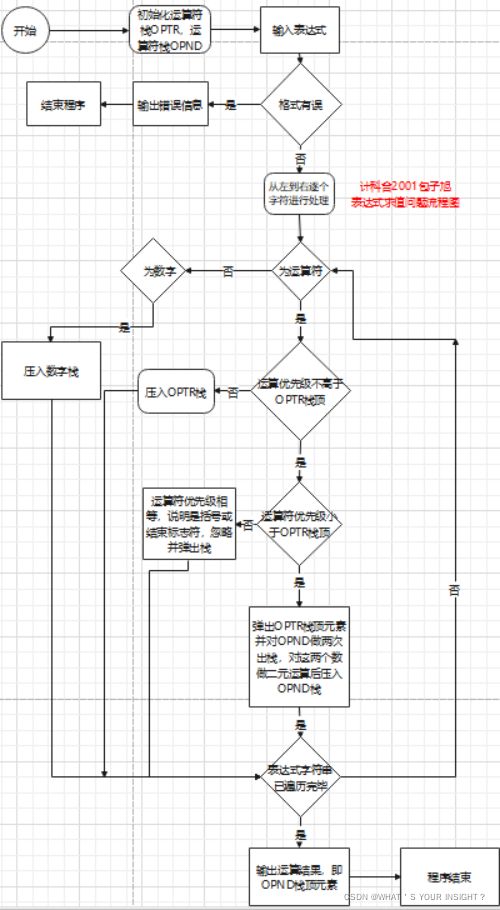
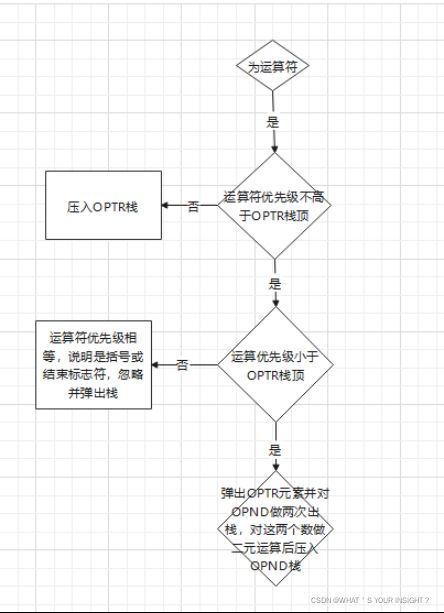
最后对表达式求值,可直接利用前面输出的逆波兰表达式来求值。遇到数字就直接进数栈,遇到操作符就与操作符栈的栈顶元素比较优先级,如果优先级大于栈顶元素,则将该操作符入栈,并读取表达式下一位。否则如果优先级小于栈顶元素,则将操作符栈顶的元素(theta)出栈,并将数字栈出栈两个数字a、b,在通过运算函数Operate(a,theta,b)把运算结果算出并重新压入数字栈,并读取表达式下一位。如果优先级相等,则将操作符栈顶元素出栈,并继续读取表达式下一位。直至表达式被读取完,此时数字栈顶储存的数字便是表达式的计算结果了,通过GetTop函数便可读取到运算结果了。
2详细设计
2.1抽象数据类型定义
ADTStack{
数据对象:D={ai|ai∈ElemSet,i=1,2,...,n,n≥0}
数据关系:R={
约定an端为栈顶,a1端为栈底。
基本操作:栈的初始化、进栈、出栈、获取栈顶元素等
}ADT Stack
ADTBinaryTree{
数据对象:D是具有相同特性的数据元素的集合
数据关系R:If D=Φ,then R=Φ;
IfD≠Φ,thenR={H};
①root唯一
②子树不相交
③关于数据元素的说明
④关于左子树和右子树的说明
⑤.........
基本操作:创建二叉树、先序遍历二叉树、中序遍历二叉树、后序遍历二叉树(非递归)等
}ADTBinaryTree
CreateBiTree(&T,definitheb)
初始条件:definition给出二叉树T的定义。
操作结果:按definition构造二叉树T。
PreOrderTraverse(T)
初始条件:二叉树T存在。
操作结果:先序遍历T,对每个结点访问一次。
lnOrderTraverse(T)
初始条件:二叉树T存在。
操作结果:中序遍历T,对每个结点访问一次。
PostOrderTraverse(T)
初始条件:二叉树T存在。
操作结果:后序遍历T,对每个结点访问一次。
2.2存储结构设计
·数据结构分为逻辑结构和存储结构
·逻辑结构与数据的存储没有关系,是独立于计算机的,是从具体问题抽象出来的数学模型。
·存储结构只有顺序存储结构和链式存储结构。
1:栈
顺序栈 (top用来存放栈顶元素的下标)
判断栈S空:如果S->top==-1表示栈空。
判断栈S满:如果S->top==Stack_Size-1表示栈满。
链栈(top为栈顶指针,指向当前栈顶元素前面的头结点)
判断栈空:如果top->next==NULL表示栈空。
判断栈满:当系统没有可用空间时,申请不到空间存放要进栈的元素, 此时栈满。
typedef struct StackNode
{
BiTNode *root;
char op;
struct StackNode *next;
} StackNode,*LinkStack;
我在使用到栈的操作的时候使用的都是链栈的存储结构,因为计算机不知道用户输入的表达式的长度,如果使用顺序储存结构的话无法提前分配储存空间。而使用链栈便可不用提前分配储存空间。并且使用链栈的储存结构还有利于插入,删除,修改操作。
2:二叉树
链式存储
二叉树的链式存储结构是指,用链表来表示一棵二叉树,即用链来指示元素的逻辑关系。 通常的方法是链表中每个结点由三个域组成,数据域和左右指针域,左右指针分别用来给出该结点左孩子和右孩子所在的链结点的存储地址 。
typedef struct BiTNode
{
char data;
int num;
struct BiTNode *lchild,*rchild;
}BiTNode,*BiTree;
在使用读取到的表达式来创建二叉树时我使用了链式结构,主要用来让根节点的左指针域指向它的左孩子,让根节点的右指针域指向它的右孩子。不过我构建的树的结构有两个数据域,char类型是用来储存操作符的,int 类型是用来储存数字的,这样构造可以省去后续将大于10的字符型数字转换为整形的麻烦。
2.3算法设计
假设输入的表达式为ch=1+2*(3-2)-2/1;Tree是一个储存树根节点的栈,再用一个栈Optr存储operand(操作符),遇到数字就创建以该数字为根的树,并且它的左孩子和右孩子都置为空,然后放到Tree栈中。遇到operaor则将其与栈顶元素比较优先级,决定是否送到输出串中,这样处理之后能得到一个后续的排列,再建立二叉树,当遇到ab+这样的建立左右接点为a和b的根为+的树并返回根接点,当遇到操作符前面只有一个操作数的如c*这样的情况就建立右子接点为c的根接点为*的,左结点为上次操作返回的子树的根接点(合并树)。
最后对表达式求值,可直接利用前面输出的逆波兰表达式来求值。遇到数字就直接进数栈,遇到操作符就与操作符栈的栈顶元素比较优先级,如果优先级大于栈顶元素,则将该操作符入栈,并读取表达式下一位。否则如果优先级小于栈顶元素,则将操作符栈顶的元素(theta)出栈,并将数字栈出栈两个数字a、b,在通过运算函数Operate(a,theta,b)把运算结果算出并重新压入数字栈,并读取表达式下一位。如果优先级相等,则将操作符栈顶元素出栈,并继续读取表达式下一位。直至表达式被读取完,此时数字栈顶储存的数字便是表达式的计算结果了,通过GetTop函数便可读取到运算结果了。
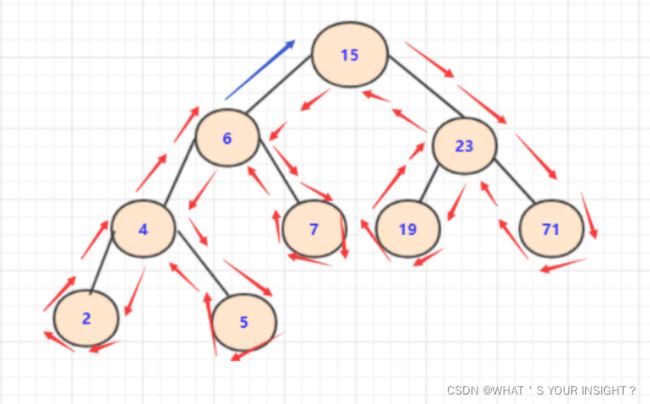
图2.3.1(算法流程图1)
图2.3.2(算法流程图2)
图2.3.3(创键的表达式二叉树)
2.3功能模块设计
程序总体分为:
- 读取用户输入的表达式功能模块
- 先序遍历二叉树表达式模块
- 中序遍历二叉树表达式模块
- 后序(非递归)遍历二叉树表达式模块
- 输出逆波兰表达式模块
- 输出表达式计算结果模块
1.读取用户输入表达式功能模块:
该模块主要用来读取用户输入的表达式,如用户输入 a+b*(c-d)-e/f#,该模块便可把用户输入的该表达式读取进去并完成建立二叉树的操作。
2.先序遍历二叉树表达式模块:
该模块可以根据模块一建立的二叉树对其进行先序遍历,即访问二叉树的顺序是根、左、右。并输出先序遍历的结果;即:-+a*b - c d /e f。
3.中序遍历二叉树表达式模块:
该模块可以根据模块一建立的二叉树对其进行中序遍历,即访问二叉树的顺序是左、根右。并输出中序遍历的结果;即:a+b*c-d-e/f。
4.后序(非递归)遍历二叉树表达式模块:
该模块可以根据模块一建立的二叉树对其进行后序遍历,即访问二叉树的顺序是左、右、根。并输出后序遍历的结果;即:a b c d - * + e f / -。
5.输出逆波兰表达式模块:
逆波兰表达式实际上就是后缀表达式,所以这个模块可以根据前面模块一创建二叉树表达式,以及模块四的后序(非递归)遍历二叉树表达式模块来实现,只需将二叉树的根地址传进来,再调用后序(非递归)遍历二叉树模块便可输出逆波兰表达式。
6.输出表达式计算结果模块:
该模块可以利用模块五输出的逆波兰表达式,读取逆波兰表达式,然后对逆波兰表达式进行运算便可输出最终结果。
3代码实现
3.1 函数清单
void InitStack (LinkStack &S);
//用于栈的初始化
void InitStack_Post(LinkStack_Post &S)
//构造一个空栈(用于后序非递归遍历)
void Push_root(LinkStack &S,BiTNode *e) ;
//树根入栈
void Push_op(LinkStack &S,char e)
//操作符入栈
void Push_Post_num(LinkStack_Post &S,int e)
//计算数字入栈
void Push_Post_data(LinkStack_Post &S,char e)
//后序非递归遍历时,将要储存的操作符入栈
BiTNode *Pop_root(LinkStack &S)
//树根结点出栈
char Pop_op(LinkStack &S)
//操作符出栈
char Pop_Post_data(LinkStack_Post &S)
//在后序非递归遍历时,将储存的操作符出栈
int Pop_Post_num(LinkStack_Post &S)
//在后序非递归遍历时将储存的数字出栈
char GetTop_op(LinkStack S)
//获取栈顶操作符
int GetTop_Post_num(LinkStack_Post S)
//获取栈顶数字,用于后序非递归遍历
char GetTop_Post_data(LinkStack_Post S)
//获取栈顶操作符,用于后序非递归遍历
char Precede(char t1,char t2)
//比较优先级函数
int In_Post(char i)
//判断输入的是否是运算符函数
int Operate(int a,char theta,int b)
//运算函数
void CreateTree_op(BiTree &T,BiTree a,BiTree b,char theta)
//创建一棵树,左孩子是a,右孩子是b,数据域是theta用来储存运算符
void CreateTree_num(BiTree &T,BiTree a,BiTree b,int theta)
//创建一棵树,左孩子是a,右孩子是b,数据域是theta用来储存数字
void CreateBiTree(BiTree &T,LinkStack &Tree,LinkStack &Optr)
//用表达式创建二叉树
void PreOrderTraverse(BiTree T) //先序递归
void InOrderTraverse(BiTree T) //中序遍历
void PostOrderTraverse(BiTree T) //后序遍历
void PostOrderTraverse_Stack(BiTree T,LinkStack_Post S1)
//后序非递归遍历
int EvaluateExpression(BiTree T,LinkStack_Post S1,LinkStack_Post &OPND)
//计算表达式结果的函数,BiTree T是构建的表达式二叉树,LinkStack_post S1用来储存数字的栈,LinkStack OPND是用来储存操作数的栈
3.2 主要函数
/**************************** 主函数 *************************************/
(完整代码在最后)
int main()
{
LinkStack Tree,Optr; //储存树节点的栈
LinkStack_Post S1,OPND; //储存数字和操作符的栈
BiTree T,Tr,Trl,Trr; //树
int sum;
InitStack(Tree);
InitStack(Optr);
InitStack_Post(S1);
InitStack_Post(OPND);
Push_op(Optr,'#');
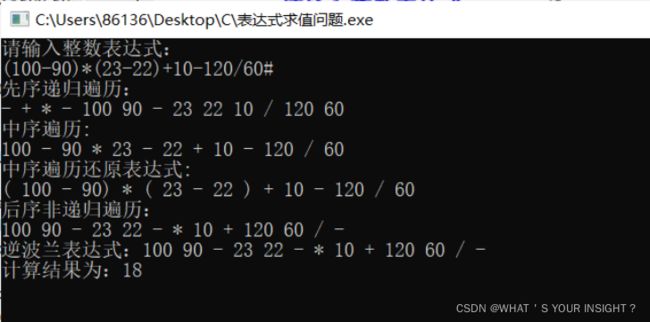
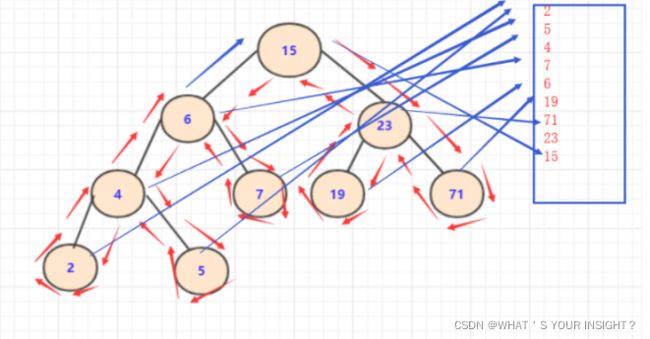
cout<<"请输入整数表达式:"< CreateBiTree(T,Tree,Optr); //创建表达式二叉树函数 T = Pop_root(Tree); cout<<"先序递归遍历:"< PreOrderTraverse(T); cout< cout<<"中序遍历:"< InOrderTraverse(T); cout< cout<<"后序非递归遍历:"< PostOrderTraverse_Stack(T,S1); cout< cout<<"逆波兰表达式:"; PostOrderTraverse(T); cout< EvaluateExpression(T,S1,OPND); //计算表达式结果函数 sum=GetTop_Post_num(OPND); cout<<"计算结果为:"< } /********************构造表达式二叉树函数***************************/ void CreateBiTree(BiTree &T,LinkStack &Tree,LinkStack &Optr) //用表达式创建二叉树 { BiTree a=NULL; BiTree b=NULL; BiTree c,d; T = NULL; char ch,theta,f; int m=0; ch = getchar(); while ((ch!='#')||(GetTop_op(Optr))!='#') { if(!In(ch)) //判断读取到的字符是不是运算符 { //字符是数字 while(!In(ch)) { ch=ch-'0'; m=m*10+ch; ch=getchar(); } if(m!=0) { CreateTree_num(T,a,b,m); Push_root(Tree,T); m=0; } } else //读取到的字符是四则运算符 { switch(Precede(GetTop_op(Optr),ch)) //判断优先级 { case '<' : Push_op(Optr,ch); ch=getchar(); break; case '>' : theta=Pop_op(Optr); c = Pop_root(Tree); d = Pop_root(Tree); CreateTree_op(T,d,c,theta); Push_root(Tree,T); break; case '=' : f=Pop_op(Optr); //用c接受下Pop的返回值,防止后面的getchar()误读 ch=getchar(); break; } } } } /*********************后序非递归函数*******************************/ void PostOrderTraverse_Stack(BiTree T, LinkStack_Post S1) //后序非递归 { //用来储存运算符合数字的栈 LinkStack S; BiTNode *p,*q; q=NULL; char a='0'; int b=0; InitStack(S); InitStack_Post(S1); p=T; while(p||S) { if(p) { if(p->lchild==NULL&&p->rchild==NULL) //判断是否是数字 { Push_Post_num(S1,p->num); }else Push_Post_data(S1,p->data); Push_root(S,p); p=p->rchild; } else { q=Pop_root(S); p=q->lchild; } } while(S1) //输出后缀表达式 { if(In_Post(GetTop_Post_data(S1))) //判断栈顶是不是运算符 {//栈顶是运算符 a=Pop_Post_data(S1); cout< }else {//栈顶是数字 b=Pop_Post_num(S1); cout< } } } /********************计算表达式结果的函数**************************/ int EvaluateExpression(BiTree T,LinkStack_Post S1,LinkStack_Post &OPND) { char theta; int a1,b1; LinkStack S; BiTNode *p,*q; q=NULL; char a='0'; int b=0; InitStack(S); InitStack_Post(S1); p=T; while(p||S) { if(p) { if(p->lchild==NULL&&p->rchild==NULL) //判断是否是数字 { Push_Post_num(S1,p->num); }else Push_Post_data(S1,p->data); Push_root(S,p); p=p->rchild; } else { q=Pop_root(S); p=q->lchild; } } while(S1) //得到计算结果栈 { if(In_Post(GetTop_Post_data(S1))) //判断栈顶是不是运算符 {//栈顶是运算符 theta=Pop_Post_data(S1); b1=Pop_Post_num(OPND); a1=Pop_Post_num(OPND); Push_Post_num(OPND,Operate(a1,theta,b1)); }else {//栈顶是数字 b1=Pop_Post_num(S1); Push_Post_num(OPND,b1); } } } 按照提示输入算术表达式及结束符后,系统会给出计算结果。 1.输入13+12*(25-21)-15/3# 后得到正确计算结果 2.输入(100-90)*(23-22)+10-120/60# 后也得到正确计算结果 3.对于非法的输入也可进行提示,也可体现程序一定的健壮性。 问题1.构造的二叉树发生错误,不能正常遍历。 问题 2.二叉树可以正确输出运算符但不能输出数字 问题 3.后序遍历出现错误,遍历的顺序不正确 问题 4.表达式计算结果出错 对于问题1.在二叉树构造中发生错误的原因是:我之前定义的二叉树的数据域是char类型,但是我在实际传的时候传的是树的结点的类型,导致类型不匹配造成了错误。当我改正了传入二叉树构造函数的参数类型时,又出现了第二个问题。 对于问题2.出现错误的原因是因为我的构造的二叉树的数据域只有char类型,这就意味着我的二叉树的叶子节点只能储存0-9的数字,对于大于等于10的数字,是不能储存的,但由于用户输入的表达式不可能只是0-9的数字,所以我重新对二叉树的节点类型修改成了 typedef struct BiTNode { char data; int num; struct BiTNode *lchild,*rchild; }BiTNode,*BiTree; 这样树的数据域有两个,一个可以用来储存操作符,另一个可以用来储存数字,这时候二叉树的叶子节点便可以储存大于等于10的整数了;但当我以为已经没问题开始运行的时候结果问题一又出现了,因为我刚开始对于构建二叉树表达式的思路是遇到数字就进入数字栈然后继续往下读取,当读取到运算符的时候比较运算符栈顶元素与当前读取到的操作符的优先级,如果小于当前读到的优先级,就让读取到的运算符进栈,否则如果大于栈顶元素的优先级,则将操作符栈顶的元素出栈,并将数字栈的两个元素出栈,并把数字栈的两个元素分别作为出栈的操作符的左孩子和右孩子。不过,想法很美好,现实却很残酷。因为数字栈里存的都只是int 型的数字,而操作符是BiTNode类型的,所以类型还是不匹配。 要想让操作符的左孩子和右孩子都是数字,还不能直接指向整型的数字,应该先将整型的数字也变成一棵树,只不过这棵树的左孩子和右孩子都指向NULL,也就是说这个数结点只有数据域用来存整型的数字。这样储存操作符的结点以及储存整数的结点就都是BiTNode类型的了。所以改进后的算法是:从表达式的开始遍历到结束,遇到数值就创建根结点数据域为该数值的二叉树,然后进栈;遇到运算符就比较优先级,比较结果是’<’的话运算符进栈,比较结果是’>’的话把上一个运算符弹出和二叉树栈弹出的树连接起来,然后再把结果进栈,比较结果是’=’的话弹出上一个运算符。最后的结果就是存储二叉树的栈中只有一个二叉树,也就是中缀表达式转换成功的二叉树。计算表达式的值是用后序遍历的的思想,遇到左右子树为空的结点说明该结点是存储的是数值,否则储存的就是操作符。 终于解决了第一个和第二个问题,成功构造了表达式二叉树。 对于问题3.出现错误的原因是因为我在写后序非递归遍历的算法的时候按照后序递归遍历的思路来写的,导致遍历结果出错。后来我才意识到后序非递归算法与前序非递归、中序非递归有所不同,并不能直接按照递归的思路写。后来我发现前序、中序、后序遍历的本质就是遍历的访问顺序不同,前序的遍历访问顺序是(根左右),发现只需将先序遍历的顺序改为根右左,如此改进后的先序访问顺序刚好与后序遍历访问的顺序相反。所以这时候刚好符合栈的先入后出的特点,所以只需要将结点在进行改进后的先序遍历前,先入栈储存起来翻转顺序。当循环结束后再遍历输出栈便可得到后序非递归遍历的结果。 (图5.1) 如图5.1便是改进后的先序遍历顺序,即先访问根节点,再访问右子树,最后访问左子树。 (图5.2) 如图5.2中蓝色矩形(栈)里从下到上存储的是改进后的先序遍历访问顺序,从此图中可以清晰看出,将栈中元素依次出栈后就是后序遍历访问的顺序了。至此后序非递归遍历二叉树表达式的问题终于解决了。 对于问题4.表达式的计算结果出错,是由于我是根据输出的逆波兰表达式进行计算的,我的思路是后序遍历输出逆波兰表达式时将输出的元素逆向的储存在另一个栈(S1)中。在这里就出现了错误,因为输出的逆波兰表达式中不仅有int 类型的数字还有char 类型的操作符,所以这个栈里的结点的数据域应该有两个,而我之前只定义了一个int型的变量; typedef struct StackNode_Post //(后序非递归遍历时所用到的栈的储存结构) { int num; //用来存数字 char data; //用来存运算符 struct StackNode_Post *next; } Stack_Post,*LinkStack_Post; 这样定义才是正确的。如此栈S1就储存了后缀表达式,只需将栈S1中的元素依次出栈进行运算即可,不过这里还有一个问题就是栈S1中的元素不仅有数字还有字符,所以在出栈的时候需要先判断栈顶的元素的类型,如果栈顶是数字,则需要用一个int类型的变量b来储存栈S1出栈的数字,并将b压入一个新的数字栈OPND中。如果栈顶是字符,则将该字符出栈,并用一个char类型的变量theta来储存这个运算符,接着将数字栈出栈两个元素,与运算符进行运算并将运算结果再次压入数字栈中。 下面是我设计的根据逆波兰表达式计算的算法: while(S1) //得到存有逆波兰表达式的栈 { if(In_Post(GetTop_Post_data(S1))) //判断栈顶是不是运算符 { //栈顶是运算符 theta=Pop_Post_data(S1); //运算符 b1=Pop_Post_num(OPND); //数字1 a1=Pop_Post_num(OPND); //数字2 Push_Post_num(OPND,Operate(a1,theta,b1)); //将运算结果重新压入数字栈中 }else { //栈顶是数字 b1=Pop_Post_num(S1); //数字从栈S1出栈 Push_Post_num(OPND,b1); //将数字压入数字栈 } } 下面是对逆波兰表达式23 34 45 * 5 6 + 7 + / +运算过程的例子: 1、 后缀表达式序列: 23 34 45 * 5 6 + 7 + / + 栈:null 2、 后缀表达式序列: 34 45 * 5 6 + 7 + / + 栈:23 3、 后缀表达式序列: 45 * 5 6 + 7 + / + 栈:23 34 4、 后缀表达式序列: * 5 6 + 7 + / + 栈:23 34 45 5、 后缀表达式序列: 5 6 + 7 + / + 栈:23 1530 6、 后缀表达式序列: 6 + 7 + / + 栈:23 1530 5 7、 后缀表达式序列: + 7 + / + 栈:23 1530 5 6 8、 后缀表达式序列: 7 + / + 栈:23 1530 11 9、 后缀表达式序列: + / + 栈:23 1530 11 7 10、后缀表达式序列: / + 栈:23 1530 18 11、后缀表达式序列: + 栈:23 85 12、后缀表达式序列: null 栈:108 在本次及课程设计中我学到了很多,因为我的这个表达式求值问题中,大量使用到了栈和树的的操作,所以我对栈和二叉树的构建的理解十分深刻。 在实现后序非递归遍历算法中我学到了多种方式来实现这个遍历: 第一种思路:对于任一结点P,将其入栈,然后沿其左子树一直往下搜索,直到搜索到没有左孩子的结点,此时该结点出现在栈顶,但是此时不能将其出栈并访问, 因此其右孩子还为被访问。所以接下来按照相同的规则对其右子树进行相同的处理,当访问完其右孩子时,该结点又出现在栈顶,此时可以将其出栈并访问。这样就 保证了正确的访问顺序。可以看出,在这个过程中,每个结点都两次出现在栈顶,只有在第二次出现在栈顶时,才能访问它。因此需要多设置一个变量标识该结点是 否是第一次出现在栈顶。 第二种思路:要保证根结点在左孩子和右孩子访问之后才能访问,因此对于任一结点P,先将其入栈。如果P不存在左孩子和右孩子,则可以直接访问它;或者P存 在左孩子或者右孩子,但是其左孩子和右孩子都已被访问过了,则同样可以直接访问该结点。若非上述两种情况,则将P的右孩子和左孩子依次入栈,这样就保证了 每次取栈顶元素的时候,左孩子在右孩子前面被访问,左孩子和右孩子都在根结点前面被访问。(它和上一种方法的区别:不是将左子树全部入栈后再转向右子树。) 第三种思路:后序遍历的顺序是左、右、根。而前序遍历的顺序是根、左、右。所以只需将前序遍历稍作改变,变成先遍历根再遍历右最后遍历左即(根右左)就会发现此时的顺序便是后序遍历的倒序了,所以这时候只需将改变后的前序遍历的每个结点压入字符栈,然后最后遍历输出字符栈。便可得到后序非递归遍历的顺序啦! 我使用的是第三种思路来完成的后序非递归的遍历。 在表达式二叉树的创建中我学到了使用合成树来创建二叉树:假设输入的表达式为ch=1+2*(3-2)-2/1;Tree是一个储存树根节点的栈,再用一个栈Optr存储operand(操作符),遇到数字就创建以该数字为根的树,并且它的左孩子和右孩子都置为空,然后放到Tree栈中。遇到operaor则将其与栈顶元素比较优先级,决定是否送到输出串中,这样处理之后能得到一个后续的排列,再建立二叉树,当遇到ab+这样的建立左右接点为a和b的根为+的树并返回根接点,当遇到操作符前面只有一个操作数的如c*这样的情况就建立右子接点为c的根接点为*的,左结点为上次操作返回的子树的根接点。 在我的表达式求值问题程序中,我还有好多idea想要加上去,比如我的程序现在还是只能计算整数,我想对我的运算函数进行改进一下,让它也可以计算小数。还有一点是当用户输入非法表达式时,我的程序会提醒用户输入表达式格式错误,但提示完后会直接结束;我想完善这部分,来实现用户输入非法格式后,给出用户提示,并可以让用户重新出入表达式,直至用户输入正确的表达式。还有想要完善的部分是,无论用户输入中缀表达式,还是前缀表达式,还是后缀表达式,计算器都可以进行计算。这个部分我已经有了很清晰的思路,如,当用户输入前缀表达式时,创建二叉树的大致思路是,从左到右读取先缀表达式,发现操作符就将其入栈,发现操作符的第二个操作数之后,将它们组织成最小的子树,然后操作符出栈,继续遍历下一个字符。在这个过程中,操作数是不入栈的,栈里只有操作符,当操作符组织成最小计算单元之后就将其出栈。当栈空的时候,说明先缀表达式遍历完毕。如,当用户输入后缀表达式时,通过后缀表达式构建二叉树,即遇到数字就创建以该数字为根的树,并将它的左孩子和右孩子都置为空,然后放到Tree栈中,遇到操作符就将tree栈中的两个元素出栈,分别作为该操作符的左孩子和右孩子构建以该操作符为根的树,并将新构建的树压入Tree栈中,如此直到读取到表达式最后一位,此时二叉树便构建完成。 因为算法与数据结构所涵盖的知识较多,所以一本书里的内容可能都需要分几个阶段去学习,难免会遗忘之前的内容。所以我会通过反复学习将前面“不求甚解”的知识消化掉,很多时候经过后面的学习,前面的一些内容就自然明了,并且会有不同的感悟。 在掌握了书上的基本操作之后,就可以尝试利用数据结构解决一些实际问题了,先学经典应用问题的解决方法,体会数据结构的使用方法,然后再做题,独立设计数据结构解决问题。 要想熟练应用就必须做大量的题,从做题中体会其中的方法。最好进行专项练习,比如线性表问题,二叉树问题,图问题。 我认为这是最高境界了,也是学习数据结构的精髓所在,我认为单独学习数据结构是无法达到这种境界的。它需要在学习算法的过程中慢慢修炼。 在学习算法的同时,逐步熟练应用、改进,慢慢体会不同数据结构和算法策略的算法复杂性,最终学会利用数据结构改进和优化算法。 该阶段已经在数据结构之上,通过在测试系统上刷各种算法题,体会利用数据结构改进优化算法。 总结:由于我们课时的原因,导致后面的课程有一部分我没有深入研究,了解的比较浅薄。我对后面的查找和排序章节很感兴趣,包括B+树、和散列表的查找,以及各种排序算法,我会在接下来的日子里,逐步掌握每一种排序,包括它们适用于什么情况,它们的时间复杂度是多少。在选题的时候我对那个走迷宫的题目很感兴趣,不过我选的时候已经被选完了,所以我准备在空闲时间写一写走迷宫的题目。并且脚踏实地一步一步完成5.6.1、5.6.2、5.6.3的目标。 最后,感觉这学期过得好快呀!还记得老师给我们上第一节课的情景,因为我的英语一直都不太好,所以刚开始还有点担心全英教学会跟不上,不过整个学期下来我感觉自己学的还不错,学到了很多英语单词,同时也收获了很多宝贵的知识。在平时课程实验报告和课程设计的完善过程中,我也遇到了这样或那样的技术问题,但经过自己的不懈努力及查阅大量的资料,最终还是成功的完成了每次任务。在上课时,您会细心地为我们讲解课上知识,下课时,也会不遗余力地为我们解答疑难问题。在本次课程设计时您也非常的细心,每次有什么问题,您都会细心地讲解,直到我们明白为止。同时我还要再次感谢翟老师抽出自己宝贵的时间来检查我的代码,因为我平时也经常帮同学们检查代码,所以我知道检查代码是一个很累的活,尤其是课设那么多的代码量。真的辛苦老师了!还记得最后一次课堂实验的报告写DFS和BFS遍历算法时,我因为写的急,导致程序仍有一点BUG就提交了,第二天,我在给室友讲解的时候才发现我出现了BUG,后来我急急忙忙的改程序,不过等我改完后,程序提交时间已经截止了。然后我告诉了您我的情况,您还是让我提交了,真的很感谢老师对我的帮助。我真的很开心能遇到您这么好的老师。 最后特别感谢翟老师您一直以来对我们的关怀与教导,再次祝您工作顺利,事事如意。 /*****************************************完整代码**************************************************/4运行与测试
5总结
5.1 程序调试中发现的问题
5.2 问题分析与解决办法
5.3 在课程设计中学到了什么
5.5 没有来得及完成的想法
5.6 未来目标
5.6.1 反复学习
5.6.2 会利用数据结构,解决实际问题
5.6.3熟练使用和改进数据结构,优化算法
5.7对老师的感谢
#include