全排列—dfs(递归算法&&手动模拟)
目录
1.dfs全排列深度优先算法思路导图
2.dfs递归思想
3.主旨展现
4.详解手动模拟
5.例题来喽
5.1例题(1)来喽——递归实现排列型枚举
5.2例题(2)来喽——递归实现指数型枚举
5.3例题(3)来喽——递归实现组合型枚举
5.4例题(4)来喽——马走日
5.5例题(5)来喽——开题顺序
5.6例题(6)来喽——找素数
1.dfs全排列深度优先算法思路导图
![]()
此图来自AC中的Hasity作者,万分感谢;
2.dfs递归思想
- dfs就是一条路走到头,当无法再往下走时就往上退一步,再看有没有路可以走,如果还没有路的话就再回退一步,重复这个步骤,直到找到可以走的道路;
- 递归的主要思想在于不断调用本身的函数,层层深入,直到遇到递归终止条件后层层回溯,其思想与dfs基本吻合,从而调用递归实现dfs;
- 正如y总讲到的回溯,它是在计算机底层执行的(系统有一个隐藏的栈帮我们做回溯),我们无法看到,也不需要操作。因此,理解并完成递归是它的一个难点;
-
时间复杂度为 O(n*n!);空间复杂度为 O(n);
3.主旨展现
- 用 a数组保存排列,当排列的长度为 n 时,是一种方案,进行输出;
- 用bool数组b表示数字是否用过。当b[i]为1时,i已经被用过,b[i] 为0时,i 没有被用过;
- dfs(i) 表示的含义是:在 a[i] 处填写数字,然后递归到下一个位置填写数字。
- 回溯:第 i 个位置填写某个数字的所有情况都遍历后, 第 i 个位置填写下一个数字。
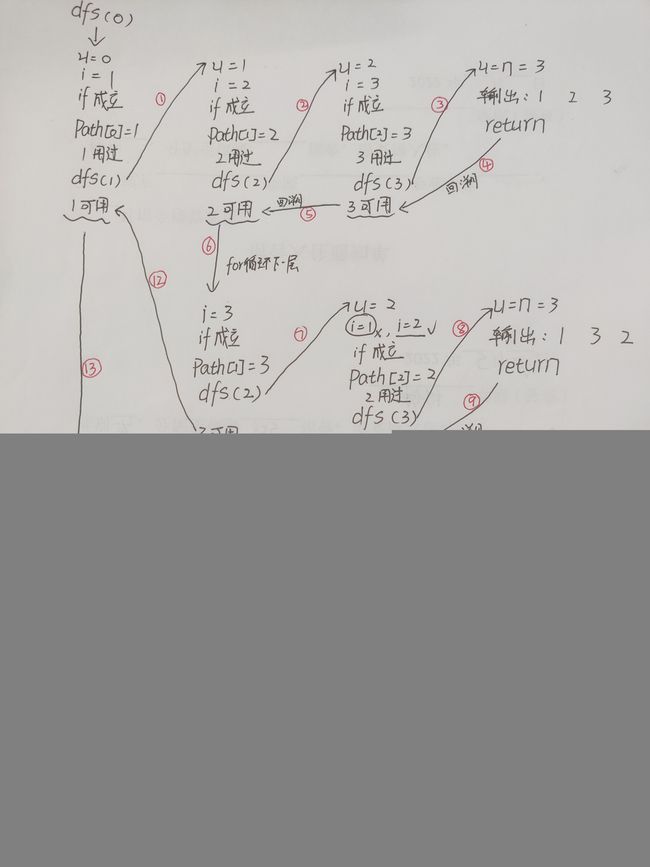
4.详解手动模拟
5.例题来喽
5.1例题(1)来喽——递归实现排列型枚举
题目描述
给定一个整数 m,将数字 1∼m 排成一排,将会有很多种排列方法。
现在,请你按照字典序将所有的排列方法输出。
输入格式
共一行,包含一个整数 m。
输出格式
按字典序输出所有排列方案,每个方案占一行。
输入样例:
3输出样例:
1 2 3 1 3 2 2 1 3 2 3 1 3 1 2 3 2 1
#include
#include
#include
using namespace std;
const int N = 20;
int a[N], m;
bool b[N];
void dfs(int x)
{
if (x == m)
{
for (int i = 0; i < m; i++)
{
cout << a[i] << " ";
}
cout << endl;
return;//回溯
}
for (int i = 1; i <= m; i++)
{
if (b[i] != true)
{
a[x] = i;
b[i] = true;
dfs(x + 1);
b[i] = false;
}
}
return;//个人感觉加上更容易理解,目的是回溯
}
int main()
{
cin >> m;
dfs(0);
return 0;
}
5.2例题(2)来喽——递归实现指数型枚举
题目描述
打印n个数中的m个数的全排列
样例输入
5 2样例输出
1 2 1 3 1 4 1 5 2 1 2 3 2 4 2 5 3 1 3 2 3 4 3 5 4 1 4 2 4 3 4 5 5 1 5 2 5 3 5 4
#include
#include
#include
using namespace std;
const int N = 20;
int a[N], n, m;
bool b[N];
void dfs(int x)
{
if (x == m)//更换输出条件
{
for (int i = 0; i < m; i++)//输出m个数
{
cout << a[i] << " ";
}
cout << endl;
return;
}
for (int i = 1; i <= n; i++)
{
if (b[i] != true)
{
a[x] = i;
b[i] = true;
dfs(x + 1);
b[i] = false;
}
}
}
int main()
{
cin >> n >> m;
dfs(0);
return 0;
}
5.3例题(3)来喽——递归实现组合型枚举
题目描述
从 1∼n 这 n 个整数中随机选出 m 个,输出所有可能的选择方案。
输入格式
两个整数 n,m ,在同一行用空格隔开。输出格式
按照从小到大的顺序输出所有方案,每行 1 个。首先,同一行内的数升序排列,相邻两个数用一个空格隔开。
其次,对于两个不同的行,对应下标的数一一比较,字典序较小的排在前面(例如 1 3 5 7 排在 1 3 6 8 前面)。
数据范围
n>0 ;0≤m≤n ;n+(n−m)≤25输入样例:
5 3输出样例:
1 2 3 1 2 4 1 2 5 1 3 4 1 3 5 1 4 5 2 3 4 2 3 5 2 4 5 3 4 5
#include
#include
#include
using namespace std;
const int N = 1e6 + 10;
int n, m, a[N], b[N];
void dfs(int x, int st, int p)
{
if (x == p)
{
for (int i = 0; i < p; i++)
{
cout << a[i]<< " ";
}
cout << endl;
return;
}
for (int i = st; i <= n; i++)//不逆序就是字典序的核心
{
if (b[i] == 0)
{
a[x] = i;
b[i] = 1;
dfs(x + 1, i + 1, p);
b[i] = 0;
}
}
}
int main()
{
cin >> n >> m;
dfs(0, 1, m);
return 0;
}
5.4例题(4)来喽——马走日
题目描述
马在中国象棋以日字形规则移动。
请编写一段程序,给定 n×mn×m大小的棋盘,以及马的初始位置 (x,y)(x,y),要求不能重复经过棋盘上的同一个点,计算马可以有多少途径遍历棋盘上的所有点。
输入格式
第一行为整数 T(T<10)T(T<10),表示测试数据组数。
每一组测试数据包含一行,为四个整数,分别为棋盘的大小以及初始位置坐标 n,m,x,yn,m,x,y。(0≤x≤n−1,0≤y≤m−1,m<10,n<100≤x≤n−1,0≤y≤m−1,m<10,n<10)。输出格式
每组测试数据包含一行,为一个整数,表示马能遍历棋盘的途径总数,00 为无法遍历一次。
输入样例
输出样例1 5 4 0 032
#include
#include
#include
using namespace std;
const int N = 1e3 + 10;
int dx[8] = { -2,-2,-1,-1,1,1,2,2 };
int dy[8] = { -1,1,-2,2,-2,2,-1,1 };
int n, m, a, b, t, ans, d[N][N];
void dfs(int a, int b, int s)
{
if (s == n * m)//是否遍历完全部象棋
{
ans++;
return;
}
for (int i = 0; i < 8; i++)
{
int x = a + dx[i], y = b + dy[i];
if (x >= 0 && x < n && y >= 0 && y < m && d[x][y] == 0)
{
d[x][y] = 1;
dfs(x, y, s + 1);
d[x][y] = 0;
}
}
}
int main()
{
cin >> t;
while (t--)
{
memset(d, 0, sizeof(d));
ans = 0;
cin >> n >> m >> a >> b;
d[a][b] = 1;
dfs(a, b, 1);
cout << ans << endl;
}
return 0;
} 5.5例题(5)来喽——开题顺序
题目描述
牛牛打 CF,已知一场比赛有 n 道题,第 i 道题的满分为 ai,时间系数为 bi,保底分为 ci,本场比赛中每次错误提交罚 p 分。即如果牛牛在第 x 分钟,这道题 y 次错误提交后通过第 i 题,他将获得 max(ci,ai−x×bi−y×p) 分。比赛持续 t 分钟,即在 t 分钟(含第 t 分钟)内做出的题目计入总分。你已经知道了他第 i 题需要花费的时间 xi 和错误提交次数 yi ,请求出牛牛可能的最大得分。输入描述
第一行三个正整数 n,t,p。(n<9。t,p<1e9)
接下来 n 行,每行 5 个正整数 a,b,c,x,y。(a,b,c,x,y<1e9)输出描述
一个正整数,表示最大的分数
样例输入
3 120 50 500 2 150 6 1 1000 4 300 12 2 1500 6 450 120 3样例输出
1266说明
方案一:先开第 3 题,在 120 分钟时切掉,得到 1500−120×6−50×3=630。此时已无法继续切题,总分 630。 方案二:先开第 1 题,在 6 分钟时切掉,得到 438 分。再开第 2 题,在 18 分钟时切掉,得到 828 分。无法切第三题,总分 1266。 方案三:先开第 2 题,在 12 分钟时切掉,得到 852 分。再开第 1 题,在 18 分钟时切掉,得到 414 分。无法切第三题,总分 1266。 故可能的最大得分为 1266。
#include
#include
#include
using namespace std;
typedef long long LL;
const int N = 1e6 + 10;
LL n, t, p, a[N], b[N], c[N], x[N], y[N], st[N];
LL res = 0, ma = 0;
void dfs(LL time)
{
if (time > t) return;
ma = max(ma, res);
for (int i = 1; i <= n; i++)
{
if (st[i] == 0)
{
st[i] = 1;
res += max(c[i], a[i] - b[i] * (time + x[i]) - y[i] * p);;
dfs(time + x[i]);
res -= max(c[i], a[i] - b[i] * (time + x[i]) - y[i] * p);;
st[i] = 0;
}
}
}
int main()
{
cin >> n >> t >> p;
for (int i = 1; i <= n; i++)
{
cin >> a[i] >> b[i] >> c[i] >> x[i] >> y[i];
}
dfs(0);
cout << ma << endl;
return 0;
} 5.6例题(6)来喽——找素数
题目描述
已知n个整数x1,x2,x3,...,xn,以及1个整数k( k < n)。从n个整数中任选k个整数相加,可分别得到一系列的和。列如当n = 4,k = 3,4个整数分别为3,7,12,19时,可得全部的组合与它们的和为:
3+7+12=22
3+7+19=29
7+12+19=38
3+12+19=34
现在,要求你计算出和为素数共有多少种
例如上例,只有一种的和为素数:3+7+19=29。输入
第一行两个空格隔开的整数n,k( 1 <= n <=20,k < n )。
第二行n个整数,分别为x1,x2,x3,...,xn( 1 <= xi <= 5 * 106)
输出
输出一个整数表示种类数。
样例输入4 3 3 7 12 19样例输出
1
#include
#include
#include
using namespace std;
typedef long long LL;
const int N = 1e6 + 10;
LL n, m, a[N], b[N], ans, res;
int cal(int x)//判断素数
{
if (x < 2) return 0;
for (int i = 2; i <= x / i; i++)
{
if (x % i == 0) return 0;
}
return 1;
}
void dfs(int x, int st, int p)
{
if (x == p + 1)
{
if (cal(res) == 1) ans++;
return;
}
for (int i = st; i <= n; i++)//避免重复
{
if (b[i] == 0)
{
res += a[i];
b[i] = 1;
dfs(x + 1, i + 1, p);
res -= a[i];
b[i] = 0;
}
}
return;
}
int main()
{
cin >> n >> m;
for (int i = 1; i <= n; i++) cin >> a[i];
//sort(a + 1, a + n + 1);//排不排序都行的
dfs(1, 1, m);
cout << ans << endl;
return 0;
}