代码随想录算法训练营day06||哈希表基础，242.有效的字母异位词，349. 两个数组的交集，202. 快乐数，1. 两数之和

哈希表理论基础 

建议：大家要了解哈希表的内部实现原理，哈希函数，哈希碰撞，以及常见哈希表的区别，数组，set 和map。  

什么时候想到用哈希法，当我们遇到了要快速判断一个元素是否出现集合里的时候，就要考虑哈希法。  这句话很重要，大家在做哈希表题目都要思考这句话。 

哈希表中关键码就是数组的索引下标，然后通过下标直接访问数组中的元素，如下图所示：

 数组就是一张 哈希表：

 那么哈希表能解决什么问题呢，一般哈希表都是用来快速判断一个元素是否出现集合里。

哈希函数

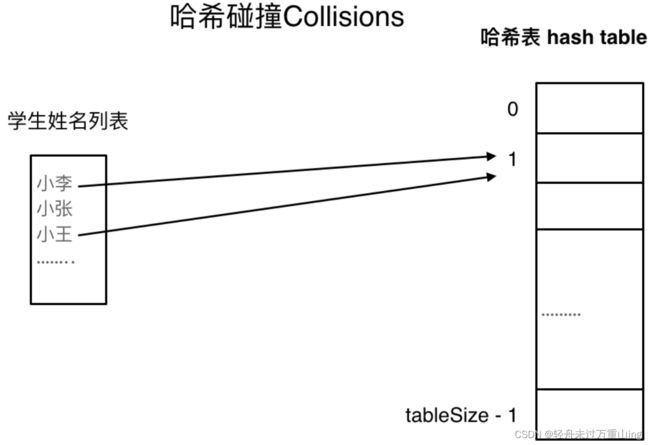
哈希函数，把学生的姓名直接映射为哈希表上的索引，然后就可以通过查询索引下标快速知道这位同学是否在这所学校里了。

哈希函数如下图所示，通过hashCode把名字转化为数值，一般hashcode是通过特定编码方式，可以将其他数据格式转化为不同的数值，这样就把学生名字映射为哈希表上的索引数字了。

如果hashCode得到的数值大于 哈希表的大小了，也就是大于tableSize了，怎么办呢？

此时为了保证映射出来的索引数值都落在哈希表上，我们会在再次对数值做一个取模的操作，这样我们就保证了学生姓名一定可以映射到哈希表上了。

此时问题又来了，哈希表我们刚刚说过，就是一个数组。

如果学生的数量大于哈希表的大小怎么办，此时就算哈希函数计算的再均匀，也避免不了会有几位学生的名字同时映射到哈希表 同一个索引下标的位置。

哈希碰撞

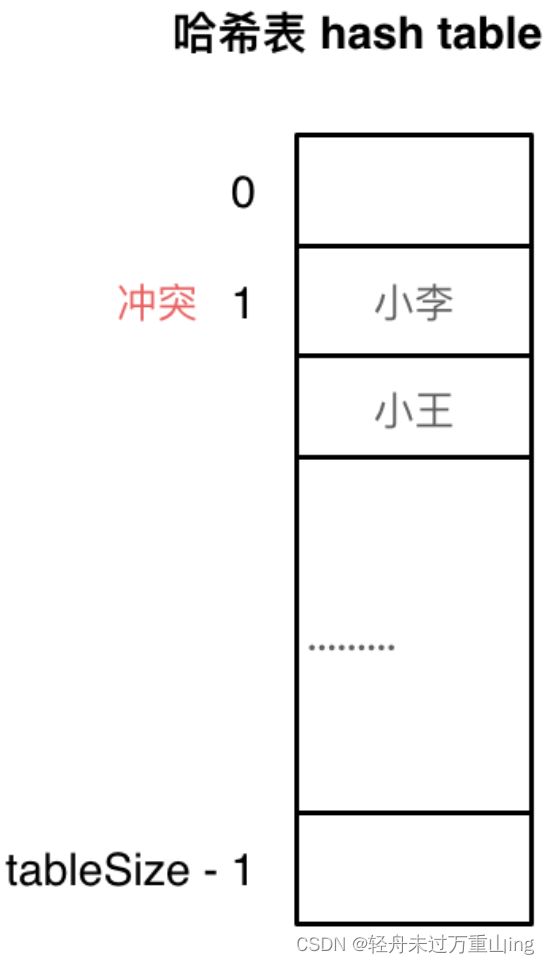
 如图所示，小李和小王都映射到了索引下标 1 的位置，这一现象叫做哈希碰撞。

 一般哈希碰撞有两种解决方法， 拉链法和线性探测法。

拉链法

刚刚小李和小王在索引1的位置发生了冲突，发生冲突的元素都被存储在链表中。 这样我们就可以通过索引找到小李和小王了

（数据规模是dataSize， 哈希表的大小为tableSize）

其实拉链法就是要选择适当的哈希表的大小，这样既不会因为数组空值而浪费大量内存，也不会因为链表太长而在查找上浪费太多时间。

线性探测法

使用线性探测法，一定要保证tableSize大于dataSize。 我们需要依靠哈希表中的空位来解决碰撞问题。

例如冲突的位置，放了小李，那么就向下找一个空位放置小王的信息。所以要求tableSize一定要大于dataSize ，要不然哈希表上就没有空置的位置来存放 冲突的数据了。如图所示：

 其实关于哈希碰撞还有非常多的细节，感兴趣的同学可以再好好研究一下

 常见的三种哈希结构

当我们想使用哈希法来解决问题的时候，我们一般会选择如下三种数据结构。

• 数组
• set （集合）
• map(映射)

 242.有效的字母异位词

给定两个字符串 s 和 t ，编写一个函数来判断 t 是否是 s 的字母异位词。

示例 1: 输入: s = "anagram", t = "nagaram" 输出: true

示例 2: 输入: s = "rat", t = "car" 输出: false

说明: 你可以假设字符串只包含小写字母。

思路：先看暴力的解法，两层for循环，同时还要记录字符是否重复出现，很明显时间复杂度是 O(n^2)。暴力的方法这里就不做介绍了，直接看一下有没有更优的方式。

 数组其实就是一个简单哈希表，而且这道题目中字符串只有小写字符，那么就可以定义一个数组，来记录字符串s里字符出现的次数。

需要定义一个多大的数组呢，定一个数组叫做record，大小为26 就可以了，初始化为0，因为字符a到字符z的ASCII也是26个连续的数值。

为了方便举例，判断一下字符串s= "aee", t = "eae"。

​

定义一个数组叫做record用来上记录字符串s里字符出现的次数。

需要把字符映射到数组也就是哈希表的索引下标上，因为字符a到字符z的ASCII是26个连续的数值，所以字符a映射为下标0，相应的字符z映射为下标25。

再遍历 字符串s的时候，只需要将 s[i] - ‘a’ 所在的元素做+1 操作即可，并不需要记住字符a的ASCII，只要求出一个相对数值就可以了。 这样就将字符串s中字符出现的次数，统计出来了。

那看一下如何检查字符串t中是否出现了这些字符，同样在遍历字符串t的时候，对t中出现的字符映射哈希表索引上的数值再做-1的操作。

那么最后检查一下，record数组如果有的元素不为零0，说明字符串s和t一定是谁多了字符或者谁少了字符，return false。

class Solution {
    public boolean isAnagram(String s, String t) {
        int[] record = new int[26];
        for(int i=0;i < s.length();i++){
            //charAt()方法可以用于提取字符串中特定位置的字符
            record[s.charAt(i) - 'a']++;// 此行求的是s字符串中对应字母的个数 
        }
        for(int i = 0;i < t.length();i++){
            record[t.charAt(i) - 'a']--;//此行求的是t字符串中对应字母的个数 
        }
        for(int count : record){//增强for循环（元素类型 变量名 ：数组或集合）
            if(count != 0){
                return false;
            }
        }
        return true; //否则就是count数组为0，俩字符串属于异位词
    }
}

时间复杂度为O(n)，空间上因为定义是的一个常量大小的辅助数组，所以空间复杂度为O(1)。 

 349. 两个数组的交集

 题意：给定两个数组，编写一个函数来计算它们的交集。

​

 说明： 输出结果中的每个元素一定是唯一的。 我们可以不考虑输出结果的顺序。

思路：

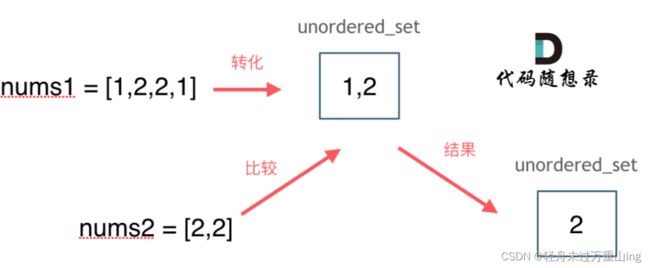
这道题目，主要要学会使用一种哈希数据结构：unordered_set，这个数据结构可以解决很多类似的问题。

注意题目特意说明：输出结果中的每个元素一定是唯一的，也就是说输出的结果的去重的， 同时可以不考虑输出结果的顺序

这道题用暴力的解法时间复杂度是O(n^2)，那来看看使用哈希法进一步优化。

那么用数组来做哈希表也是不错的选择，例如上题242题中；

但是要注意，使用数组来做哈希的题目，是因为题目都限制了数值的大小。

而这道题目没有限制数值的大小，就无法使用数组来做哈希表了。

而且如果哈希值比较少、特别分散、跨度非常大，使用数组就造成空间的极大浪费。

此时就要使用另一种结构体了，set ，关于set，C++ 给提供了如下三种可用的数据结构：

• std::set
• std::multiset
• std::unordered_set

std::set和std::multiset底层实现都是红黑树，std::unordered_set的底层实现是哈希表， 使用unordered_set 读写效率是最高的，并不需要对数据进行排序，而且还不要让数据重复，所以选择unordered_set。

​

拓展

那有同学可能问了，遇到哈希问题我直接都用set不就得了，用什么数组啊。

直接使用set 不仅占用空间比数组大，而且速度要比数组慢，set把数值映射到key上都要做hash计算的。

不要小瞧 这个耗时，在数据量大的情况，差距是很明显的。

class Solution {
    public int[] intersection(int[] nums1, int[] nums2) {
        //第一种方法：使用HashSet来做
        if(nums1 == null || nums1.length == 0 || nums2 == null || nums2.length ==0){
            return new int[0];
        }
        Set set1 = new HashSet<>();//定义一个HashSet集合存放数组nums1
        Set resSet = new HashSet<>();//定义一个HashSet结果集合，存放最终结果
        //遍历数组1
        for(int i : nums1){//增强for循环,i按顺序返回的是nums1数组的每个值，不含下标
            set1.add(i);//调用add();方法加入到set1集合中
        }
        //遍历数组2的过程中判断哈希表中是否存在该元素
        for(int i : nums2){
            if(set1.contains(i)){ 
            //调用集合的contains()方法，判断是否含i这个元素（也即nums2中的元素）
                resSet.add(i);//若有，则加到resSet集合中
            }
        }
        //方法1：将结果集合转为数组（没用过，补充学习一下）
       // return resSet.stream().mapToInt(x -> x).toArray();

        //方法2：另外申请一个数组存放setRes中的元素,最后返回数组
        int[] arr = new int[resSet.size()];
        int j = 0;
        for(int i : resSet){
            arr[j] = i;
            j++; 
            //也可以直接写成arr[j++] = i;
        }
        return arr;
    }
}

后记

本题后面 力扣改了 题目描述 和 后台测试数据，增添了 数值范围：

• 1 <= nums1.length, nums2.length <= 1000
• 0 <= nums1[i], nums2[i] <= 1000

所以就可以 使用数组来做哈希表了， 因为数组都是 1000以内的。

class Solution {
    public int[] intersection(int[] nums1, int[] nums2) {
        //第二种方法：规定数组范围之后，可以选择使用Hash数组来做
        int[] hash1 = new int[1005]; //初始化一个长为1005的数组，数值全为0
        int[] hash2 = new int[1005]; //初始化一个长为1005的数组，数值全为0
        for(int i : nums1){//增强for循环，i按循序返回nums1
            hash1[i]++;//让nums1中出现的数在hash1数组中做记录，有值就让那一位+1
        }
        for(int i : nums2){
            hash2[i]++;
        }
        List resList = new ArrayList();
        for(int i = 0;i < 1002; i++){
            if(hash1[i] > 0 && hash2[i] > 0){//满足这俩条件说明i这个值，俩数组都有！
                resList.add(i);
            //把i值加到新的集合里面，这里还选用ArrayList集合，  
            //因为往数组末尾添加元素，效率不受影响，这里使用了泛型，只能存储Integer类型数据
            }
        }
        int index = 0;
        int[] res = new int[resList.size()];//定义一个新的数组，把resList集合里的值传进去
        for(int i : resList){
            res[index++] = i;//通过增强for循环，把resList中的值添加给到res数组
        }
        return res;
     }
}

补充一些点：

泛型：List resList = new ArrayList();

使用了泛型List之后，表示List集合中只允许存储Integer整型的数据

总结:
①没有使用泛型每次元素返回的都是Object类型的元素,Object中没有我们想要返回的类型的方法，所以需要强转.使用了泛型之后调父类中的方法不需要转型了,使用迭代器的时候表示迭代器迭代的是泛型类型的了.但是要注意如果要调用子类中特有的方法,仍然需要向下转型.
②指定了泛型之后,只能往集合里面存储泛型的这种数据类型,或者他的子类.元素类型被统一了
 

ArrayList的优点:
①数组这种数据结构检索元素效率高.每个元素在空间中的内存地址是有序且连续的,并且数据类型所占空间大小一样,
所以知道第一个元素的下标和内存地址,可以通过一个数学表达式来计算出任意一块内存地址对应到下标,找到元素.
ArrayList的缺点:
 - 数组的增减效率低,当要随机增加或者删除某个元素时,就涉及到后面的元素的位移,所以效率较低.
 - 数组中不能存储大量的数据,因为数组是连续的,在空间中很难开辟出一大块连续的内存空间.
需要注意的一点:
   - 在数组的最后一个元素处进行增减操作效率还是较高.（所以这里选用了ArrayList集合）

202. 快乐数

思路：

算法分为两部分，我们需要设计和编写代码。

• 给一个数字 nnn，它的下一个数字是什么？
• 按照一系列的数字来判断我们是否进入了一个循环。

第 1 部分我们按照题目的要求做数位分离，求平方和。☆☆☆

第 2 部分可以使用哈希集合完成。每次生成链中的下一个数字时，我们都会检查它是否已经在哈希集合中。

如果它不在哈希集合中，我们应该添加它。
如果它在哈希集合中，这意味着我们处于一个循环中，因此应该返回 false。

我们使用哈希集合而不是向量、列表或数组的原因是因为我们反复检查其中是否存在某数字。检查数字是否在哈希集合中需要 O(1)的时间，而对于其他数据结构，则需要 O(n)的时间。选择正确的数据结构是解决这些问题的关键部分。

class Solution {
    public boolean isHappy(int n) {
        //使用HashSet
        /**
        根据我们的探索，我们猜测会有以下三种可能。
        1.最终会得到 111。
        2.最终会进入循环。
        3.值会越来越大，最后接近无穷大。(不用处理，但是最好理解为什么)
         */
        Set record = new HashSet<>(); //定义一个HashSet()集合
        while(n != 1 && !record.contains(n)){
            //判断n不等于 且 record集合中也没有出现n，则执行
            record.add(n); //输入要判断的数n
            n = getNextNumber(n);//调用构造方法getNextNumber来计算 数位分离和
        }
        return n == 1;//此处不能写true，用例n = 2时会不通过
    }
        private int getNextNumber(int n){//构造一个私有方法getNextNumber
            int sum = 0; //定义一个变量用来存sum
            while(n > 0){
                int temp = n % 10;//得到个位数字
                sum += temp * temp; //将个位数字计算平方和并累计到和res中去
                n = n / 10;//紧接着计算十位数字，然后进入while循环条件
                          //如此反复，可以计算res = 数位分离的平方和 
            }
        return sum;
        }
}

1. 两数之和 

给定一个整数数组 nums 和一个目标值 target，请你在该数组中找出和为目标值的那 两个 整数，并返回他们的数组下标。

你可以假设每种输入只会对应一个答案。但是，数组中同一个元素不能使用两遍。

示例:给定 nums = [2, 7, 11, 15], target = 9 ；因为 nums[0] + nums[1] = 2 + 7 = 9；所以返回 [0, 1]

 思路：

很明显暴力的解法是两层for循环查找，时间复杂度是O(n^2)。

做本题之前最好了解一下这两题：

242.有效的字母异位词，这道题目是用数组作为哈希表来解决哈希问题，

349.两个数组的交集，这道题目是通过set作为哈希表来解决哈希问题。

解决四个问题：

①为什么 会想到使用哈希表 ②哈希表为什么 要用map

③本题中map究竟是用来做什么的（存放遍历过的元素的）

④map里面的key和vlaue是用来存什么的

首先强调什么时候使用哈希法：当我们需要查询一个元素是否出现过，或者一个元素是否在集合里的时候，就要第一时间想到哈希法。        

本题呢，我就需要一个集合来存放我们遍历过的元素，然后在遍历数组的时候去询问这个集合，某元素是否遍历过，也就是  是否出现在这个集合。

那么我们就应该想到使用哈希法了。

因为本题，我们不仅要知道元素有没有遍历过，还要知道这个元素对应的下标，需要使用 key value结构来存放，key来存元素，value来存下标，那么使用map正合适。

再来看一下使用数组和set来做哈希法的局限。

• 数组的大小是受限制的，而且如果元素很少，而哈希值太大会造成内存空间的浪费。
• set是一个集合，里面放的元素只能是一个key，而两数之和这道题目，不仅要判断y是否存在而且还要记录y的下标位置，因为要返回x 和 y的下标。所以set 也不能用。

此时就要选择另一种数据结构：map ，map是一种key value的存储结构，可以用key保存数值，用value再保存数值所在的下标。 

 这道题目中并不需要key有序，选择std::unordered_map 效率更高！ 使用其他语言的同学注意了解一下自己所用语言的数据结构就行。

接下来需要明确两点：

• map用来做什么
• map中key和value分别表示什么

map目的用来存放我们访问过的元素，因为遍历数组的时候，需要记录我们之前遍历过哪些元素和对应的下标，这样才能找到与当前元素相匹配的（也就是相加等于target）

接下来是map中key和value分别表示什么：

这道题 我们需要 给出一个元素，判断这个元素是否出现过，如果出现过，返回这个元素的下标。

那么判断元素是否出现，这个元素就要作为key，所以数组中的元素作为key，有key对应的就是value，value用来存下标。

所以 map中的存储结构为 {key：数据元素，value：数组元素对应的下标}。

在遍历数组的时候，只需要向map去查询是否有和目前遍历元素匹配的数值，如果有，就找到的匹配对，如果没有，就把目前遍历的元素放进map中，因为map存放的就是我们访问过的元素。

class Solution {
    public int[] twoSum(int[] nums, int target) {
        int[] res = new int[2]; //定义一个数组用来存放 两个整数的下标
        //先判断一下，不一定有
        if(nums == null || nums.length ==0){ //空数组或者长度为0
            return res;
        }
        Map map = new HashMap<>();//定义一个HashMap
        for(int i = 0; i 

这里用到了map的两个方法：

map.containsKey(temp)){//判断map中是否包含某个key（这里就是temp）

map.get(temp);//get()方法，通过key获取value，这里就是获取元素值为temp的下标

本题其实有四个重点：①②③④把这四点想清楚了，本题才算是理解透彻了。

很多录友把这道题目 通过了，但都没想清楚map是用来做什么的，以至于对代码的理解其实是 一知半解的。