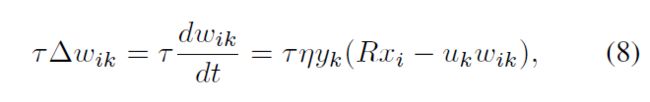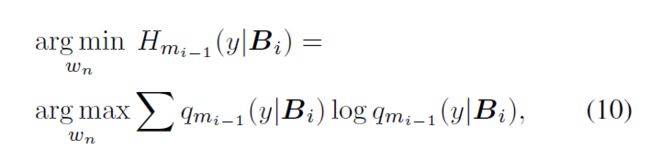神经调节的Hebbian学习用于完全测试时自适应

摘要

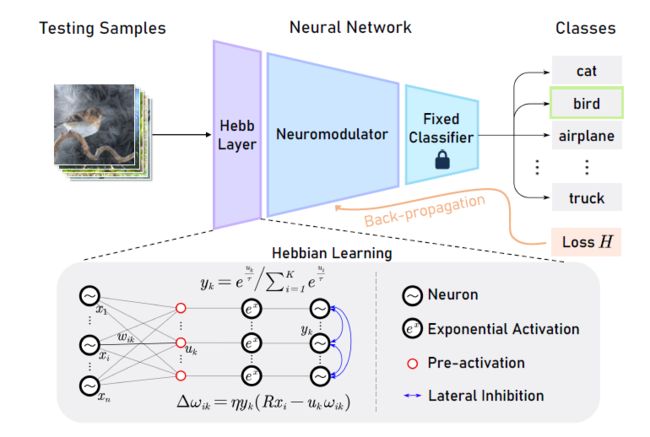
完全测试时自适应（Fully test-time adaptation）是指在推理阶段对输入样本进行序列分析，从而对网络模型进行自适应，以解决深度神经网络的跨域性能退化问题。我们从生物学合理性学习中获得灵感，其中神经元反应是基于局部突触变化过程进行调整的，并由竞争性侧抑制规则激活。基于这些前馈学习规则，我们设计了一个软Hebbian学习过程，为Test-Time adaption 提供了一种无监督的有效机制。我们观察到，通过加入反馈神经调节层，这种前馈Hebbian学习完全适应测试时间的性能可以显著提高。它能够基于由顶层推理层的误差反向传播产生的外部反馈对神经元的响应进行微调。这导致了我们提出的神经调节的Heb-bian学习(NHL)方法完全适应测试时间。将无监督前馈软Hebbian学习与学习神经调节器相结合，从外部响应中获取反馈，可以在测试过程中有效地适应源模型。在基准数据集上的实验结果表明，我们提出的方法可以显著提高网络模型的自适应性能，优于现有的最先进的方法。

背景

为了解决在域迁移中性能下降问题，提出了无监督域自适应(UDA)[16,38,50]，利用大量未标记的测试数据以无监督的方式对模型参数进行微调。

Source-free UDA

介绍

Source-free UDA方法[33,35,67]的目的是在不需要访问源域样本的情况下调整网络模型。Source-free UDA 有两种主要类别。第一类需要访问目标域上的整个测试数据集来实现它们的自适应性能[35,67]。第二种方法称为完全测试时适应（Fully test-time adaption,FTTA），它只需要访问测试样本的实时流[41,64,66]，它能够在测试过程中动态地适应源模型。现有的完全测试时间自适应方法主要集中在构造各种损失函数来调节推理过程和基于误差反向传播的自适应模型。

e.g

TENT 通过最小化熵损失来更新批处理规范化模块

TTT 根据代理学习任务上的自监督损失更新特征提取器参数

TTT++ 介绍了一种基于在线矩匹配的特征对齐策略

挑战

早期通过浅层特征表示 在后面捕获后期特征对观察到的输入的潜在解释因素发挥了重要作用.

例如，在深度神经网络模型中，网络的早期层倾向于对角落、边缘或颜色做出响应。相比之下，更深的层响应更多特定于类的特征[72]。

在corruption test-time adaptation场景中，特定于类的特征总是相同的，因为测试数据集是训练域的corruption。然而，模型的早期层可能由于corruption而失效。

fully test-time UDA的核心挑战在于如何在没有监督的情况下学习测试样本的有用的早期层表示。

人们已经认识到，使用反向传播的监督式端到端深度神经网络训练的学习规则与神经生物学中早期前端神经处理的学习规则是不相关的[28]。在真实的生物神经网络中，神经元的反应是基于突触前细胞和突触后细胞的局部活动，加上一些衡量任务执行情况的全局变量来调整的，而不是其他特定神经元的活动[69]。

Hebbian Learning

Hebbian Learning 规则的思想背后是，当两个神经元反复共同激活，它们之间的连接应该被加强，因为这种共同激活可能反映了它们之间存在的关联。需要注意的是，Hebbian Learning 规则并不考虑激活是否导致神经元的输出。它仅仅关注在时间上相邻的激活之间的关联。实际上，Hebbian Learning 可能导致网络的过度连接，因此在实际应用中，通常还需要考虑其他形式的学习规则来调整神经网络的连接。

Hebbian学习的目的是在没有监督的情况下，基于局部突触可塑性规则学习有用的早期层表示，它能够生成与端到端有监督的反向传播训练学习的早期表示一样好的早期表示。Hebbian学习是一个纯粹的feed-forward adaption 过程，不需要来自遥远的顶层网络层的反馈。

具体来说，学习过程中突触强度的局部变化与突触前细胞的活性成正比它还在一层内的神经元之间引入了局部侧抑制，在那里，具有强烈反应的隐藏单元的突触被推向驱动它们的模式，而那些反应较弱的突触则被推离这些模式。

如图1，第一行显示原始图像。第二行显示了目标域中具有严重图像损坏的图像。第三行显示了在源域中训练的网络模型为这些目标域图像学习到的特征映射。第四行是我们的Hebbian学习方法学习到的特征映射。最后一行(“oracle”)显示了用真实标签学习到的特征映射。我们可以看到，无监督的Hebbian学习能够生成和监督学习一样好的特征图。

相关工作

Test-time Adaptation

测试时间自适应的目的是在目标域测试输入样本的同时，对训练好的模型进行在线自适应。

TTT, TTT+, TENT, DUA, 

Source-free Unsupervised Domain Adaptation

Source-free Unsupervised Domain Adaptation 旨在使源模型适应未标记的目标域，而无需访问源域的数据。

SHOT, 3C-GAN, G-SFDA, CPGA, HCL, DIPE,SFDA-DE

Domain Generalization

领域泛化的目的是只在源数据上训练模型，这些源数据可泛化到看不见的目标领域.

Unsupervised Hebbian Learning

在传统的端到端训练中，通常使用反向传播来更新深度神经网络的权值。人们已经认识到，使用反向传播的有监督的端到端深度神经网络训练的学习规则与神经生物学中早期前端神经处理的学习规则有很大不同。同时有监督学习需要大量的标签。

贡献

首先，原来的竞争学习的original hard decision不适合FTTA。其次，Hebbian学习没有一个有效的机制来考虑外部反馈，特别是来自网络顶层的反馈。受此启发，在这项工作中，我们建议开发一种新的方法，称为神经调节Hebbian学习(neuro-modulated Hebbian learn-ing, NHL)，用于完全适应测试时间.我们首先在前馈Hebbian学习中加入软决策规则，以改善其竞争性学习。其次，我们学习了一个神经调节器neuro-modulator来捕获来自外部响应的反馈，它控制哪一类型的特征被巩固并进一步处理以最小化预测误差。在推理过程中，源模型根据所提出的NHL规则对推理过程中的每个小批量测试样本进行adapt。

(1)研究发现，早期层表征的有效无监督学习是完全测试时间适应的主要挑战，并探索了神经生物学启发的软Hebbian学习，以实现有效的早期层表征学习和完全测试时间适应。

(2)提出了一种新的神经调制Hebbian学习方法，该方法将无监督前馈Hebbian早期层表示学习与学习神经调节器相结合，以捕获外部响应的反馈。我们分析了基于自由能原理的NHL算法的最优特性[14,15]。

方法

Problem Formulation

source distribution: Xs, Ys

target distribution: Xt, Yt

拥有参数θ的m(θ)模型是在数据 Xs  上训练的，由特征提取器feature extractorF和分类器C组成。

我们的目标是在测试过程中以无监督的方式调整训练好的模型m。给定输入样品批次序列{B1, B2，…， Bn}，网络模型的第i次自适应只能依赖于第i批测试样本Bi。

模型m 被当作先验，因此，在给定先验模型pm(y)的情况下，预测目标样本的标签变成一个Bayesian后验qm(y|B1) 用于第一个batch。在第一个adaption batch之后，先验模型m会更新成m1这个贝叶斯推理过程在所有后续批次中重复，并产生最终的后验估计 。其中mn−1表示前n−1批连续自适应后的先验模型。

Overview of Our NHL Method

我们提出的神经调节的Hebbian学习包括两个主要部分:feed-forward soft Hebbian learning layer和neuro-modulator

feed-forward soft Hebbian learning layer

目的是基于局部突触可塑性和软竞争学习规则，在没有监督的情况下学习有用的早期层表示。

然而，我们认识到，仅仅是前馈Hebbian学习并不能像目前最先进的方法那样达到完全适应测试时间的竞争性性能。我们发现它缺乏有效响应外部刺激的能力，特别是来自网络输出层的反馈。

neuro-modulator layer

为了解决↑的问题，我们建议在网络的软feed-forward soft Hebbian learning layer和分类器模块之间设计一个神经调节器层、中间层或接口。它充当了两种不同学习方法之间的桥梁:前馈Hebbian学习和原始误差反向传播。（这两个都很重要） 这可以通过自下而上的前馈生成过程(如我们的Hebbian学习层)与自上而下的基于反馈的优化过程(如我们的神经调节器)相结合的并发预测过程来实现。

输入 xt，假设xt是通过environment causes ϑ生成的，写作p(xt) = p(xt, ϑ)自由能原理指出，大脑编码的识别密度高于感官原因，它将生成概率混合优化为q1(xt) := q1(xt, ϑ). 另一方面，通过后验q2(y) := q2(y|Xt) 近似真实分布 p(y|Xt)

我们可以通过以下Kullback-Leibler (KL)散度来衡量这两个分布之间的相似性

根据Bogacz[3]的分析，KL散度 的最小化可以转化为自由能F的最大化，定义为:

*KL散度 

是两个概率分布之间的差异或相似度的一种度量，用于衡量一个概率分布相对于另一个分布的“距离。

给定两个离散概率分布P和Q，它们对相同的事件空间进行建模，KL散度定义为：

其中，P(i)和Q(i)分别是事件i在分布P和Q中的概率。KL散度的值越小，表示两个分布越相似；值越大，表示它们之间的差异越大

将KL散度的定义与自由能的表达式联系起来。考虑一个概率分布P，我们希望找到一个近似的分布Q，使得DKL​(P∣∣Q)最小。这可以通过最大化以下表达式来实现

这个表达式与KL散度的定义形式上是相似的，但符号相反。现在，我们可以将其与自由能的表达式联系起来

Feed-Forward Soft Hebbian Learning

早期前馈层的目的是在没有任何监督的情况下学习输入的有用层表示。这个问题的近似解决方案可以简化为寻找输入数据的第一个主成分[47]，称为Oja规则*及其变体。(Oja规则的本身是一个Hebbian规则的变体+归一化条件)

在Oja规则中，连接输入xi的突触前神经元i和激活yk的突触后神经元k的突触权wik的可塑性定义为:

我们认识到这个过程缺乏通过网络中不同的隐藏单元来检测数据的不同特征的能力。 通过考虑定义一组权重通过生成模型来优化与输入数据的分布相似度。

我们假设目标域输入 Xt 是通过分布为pt(x)的隐藏causes ϑ 生成的，我们用q(x|w)定义pt(x)的近似，条件是权重w。此外，我们使用混合指数函数来定义概率。其中，wk是与突触后神经元k对应的权向量，N是一个归一化因子，以确保q是一个概率度量。在该生成模型中，目标函数由Kullback-Leibler (KL)散度KL[pt(x)|q(x|w)]给出。可以看出，优化kl -散度的最优参数向量与输入分布的均值成正比[45]。另一方面，公式(5)对应于神经解释作为归一化权值为wk/R的激活函数，其中R为权向量wk的范数。这个式子是 softmax 函数的一种表达形式，用于定义一个由权重向量 wk​ 参数化的概率分布。

在我们的软Hebbian学习中，对于有K个神经元的网络层，我们定义第K个神经元的输出为↓。其中UK是第k个神经元的加权输入，如UK = wik·xi·τ是一个温度标度超参数。

补充

这就产生了一个新的软Hebbian塑性规则↓。式中η为学习率。可以证明，利用式(7)中的塑性规则更新权值，它们可以收敛到半径为R的球内的平衡点。

去证明它们可以收敛到半径为R的球内的平衡点， 我们重写（7）↓

其中常数τ定义了学习动力学（learning dynamics）的时间尺度。权向量范数（norm of the weight vector）的导数为:

有了这个，我们可以看到权向量的范数收敛到半径为R的球体。这是因为当||wk||> R时，权值的范数减小，当||wk||< R时，权值的范数增大。

Oja规则*   

Oja's规则是一种用于人工神经网络的学习规则，主要用于无监督学习场景中线性神经元的训练。具体而言，Oja's规则在主成分分析（PCA）中使用（居然这么传统），用于调整神经元的权重，以捕捉输入数据的主成分。该规则是希伯学习（Hebbian learning）的一种形式，其基本思想是当神经元同时激活时，它们之间的连接会加强。Oja's规则旨在实施神经元之间的竞争机制，促使学习输入数据的最信息化组成部分。

术语 xi​⋅y 表示输入分量 xi​ 和神经元输出之间的相关性。减法项 α⋅wi​ 引入了竞争机制，防止任何单个权重增长过大。

权向量范数（norm of the weight vector）

"Weight vector"（权重向量）的范数（norm）是一个表示该向量大小的数值。在神经网络中，每个神经元都有一个关联的权重向量，这个向量的范数通常用于衡量该神经元的权重参数的大小。

权重向量的范数的导数通常涉及到使用梯度下降或其变体来调整模型的参数（包括权重），以最小化或最大化某个损失函数。权重向量的范数的导数可以用来计算梯度，指导我们调整权重以使损失函数最小化。

The Neuro-Modulation Layer

单独的软Hebbian学习不会自动导致p(y|Xt)的完美后验估计，这是因为它没有一个有效的机制来考虑外部反馈，特别是来自网络顶层的反馈。我们提出的解决方案是结合一个或多个调制层来引导权重更新到期望的结果[17,36]。

如式(3)所定义，q2(y)及其真后验p(y|Xt)的kl -散度最小化问题可根据自由能原理表示为↓，其中是归一化项。注意这一项并不依赖于q2(y)， 因此，最小化kl散度被简化为最大化F，因此给定批数据Bi的标签y，它可以被话简称最小化似然函数。

在FTTA过程中，sample labels不可用。因此，取而代之，我们基于一个近似后验 qmi−1 (y|Bi) 最小化每个batch Bi的y的熵。因此，神经调制层训练过程中需要优化的损失函数为↓。其中，wn为实现神经调节器的层中的权值。在现有的深度神经网络训练中，我们可以使用梯度下降来优化这些权重。

实验

数据集

CIFAR10/100-C

ImageNet- C

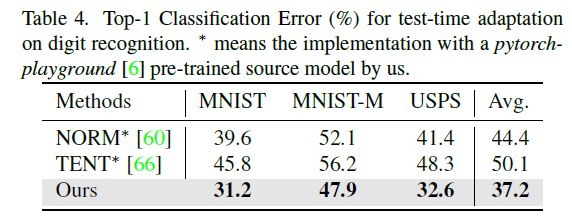
SVHN→MNIST/MNIST-M/USPS

对比方法

基线模型只在源数据上进行训练，在测试过程中没有进行任何微调。

TTT

NORM

TENT

DUA

实现细节

我们使用基于RobustBench协议的所有主干的TENT或DUA正式实现的预训练模型权重[9]。

对于数字识别转移任务，我们使用了来自 pytorch-playground 的SVHN的预训练模型权值

batch size：128

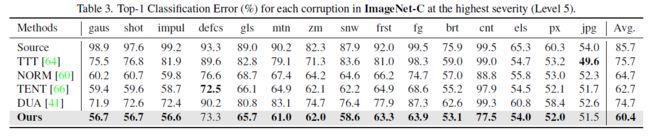
实验结果

总结

在这项工作中，我们从生物神经调节过程中获得灵感，构建了一个新的神经调节的Hebbian学习(NHL)框架。将无监督前馈软Hebbian学习与学习神经调节器相结合，从外部响应中获取反馈，可以在测试过程中有效地适应源模型。在基准数据集上的实验结果表明，我们提出的方法可以显著降低带有损坏的图像分类的测试误差，达到新的最先进的性能。