实验三 RSA密码算法的设计与实现

✅作者简介：CSDN内容合伙人、信息安全专业在校大学生
系列专栏 ：简单外包单
新人博主 ：欢迎点赞收藏关注，会回访！
舞台再大，你不上台，永远是个观众。平台再好，你不参与，永远是局外人。能力再大，你不行动，只能看别人成功！没有人会关心你付出过多少努力，撑得累不累，摔得痛不痛，他们只会看你最后站在什么位置，然后羡慕或鄙夷。

---

实验三 RSA密码算法的设计与实现

一、实验目的

设计并实现RSA密码算法，深入理解非对称密码算法RSA的加密和解密过程，提高学生利用对非对称密码算法解决实际问题的能力。

二、实验任务

（1）设计并实现RSA加解密算法，提供图形界面；（必做）
（2）完成公、私钥生成、文本加解密功能，并记录运行时间，使用DES算法加密相同的文字，比较两种算法加密的速度。（必做）
（3）基于RSA算法，完成对文件的加解密（扩展）；提供程序核心代码并撰写实验报告。

三、实验环境

信息楼西505，Windows10，python3.9.7

四、实验原理

1. RSA加密原理：

1. 任意选取两个大素数,计算
2. 任意选取一个大整数e, 满足,整数e用作公钥
3. 确定私钥d, 满足
4. 若M为待加密对象，
5. 解密

2. 扩展欧几里得算法求逆元

若a与b互质，那么, 即 ax + by = 1, 于是 by = (-x)a+1
也即：by=1(mod a)，于是y即为b在模a意义下的乘法逆元。在欧几里得算法中，可以把过程写的更清晰一些：（仍以为例）

带入得：

于是，据此可以构建一个表格来计算乘法逆元

图 1 乘法逆元

图 2 实现的核心代码

3. 快速幂指数算法

在RSA中，加、解密过程都是要求某个整数的整数次幂后再取模。大多时候，这两个整数都会比较大，这时候直接按含义来进行计算时得到的中间结果会超出计算机所允许的整数取值范围（例如计算66^77，这还是比较小的）所以需要一种算法较快地计算 a^p (mod n) 快速幂算法能帮我们算出指数非常大的幂，传统的求幂算法之所以时间复杂度非常高（为O(指数n)），就是因为当指数n非常大的时候，需要执行的循环操作次数也非常大。所以我们快速幂算法的核心思想就是，将指数二进制展开，每一步都把指数分成两半，而相应的底数做平方运算。这样不仅能把非常大的指数给不断变小，所需要执行的循环次数也变小，而最后表示的结果却一直不会变。实现的流程图如下：

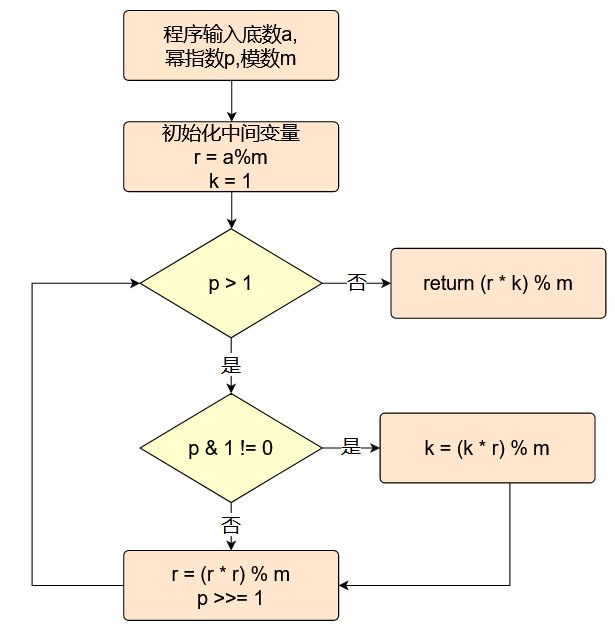
图 3 快速幂指数流程图

五、程序设计核心代码

生成密钥对模块 (generate_keypair):
计算 n 和 φ(n)，其中 n = p * q，φ(n) = (p-1) * (q-1)。
选择公钥 e，确保 e 和 φ(n) 互质。
计算私钥 d，满足 (e * d) % φ(n) = 1。
返回公钥 (n, e) 和私钥 (n, d)。

1. def generate_keypair(p,q):

3. # 计算 n 和 φ(n)  
   

4. n = p * q  
   

5. phi_n = (p - 1) * (q - 1)  
   

7. # 选择公钥 e，确保 e 和 φ(n) 互质  
   

8. print("正在生成公钥 e")  
   

9. e = generate_coprime(phi_n)  
   

11. # 计算私钥 d，使得 (e * d) % φ(n) = 1  
    

12. print("正在计算私钥 d")  
    

13. d = mod_inverse(e, phi_n)  
    

15. **return** ((n, e), (n, d))  
    

生成大素数模块 (generate_large_prime):
使用 random.getrandbits(64) 生成一个64位的随机整数。
使用 Miller-Rabin 素性测试判断是否为素数，循环直至找到素数。

1. def generate_large_prime():

2. **while** True:  
   

3.     num = random.getrandbits(64)  
   

4.     **if** is_prime(num):  
   

5.         **return** num  
   

素性测试模块 (is_prime):
使用 Miller-Rabin 素性测试判断一个数是否为素数。
设置默认的迭代次数 k 为5。

1. def is_prime(n, k=5):

2. # Miller-Rabin 素性测试，可根据需要调整参数 k  
   

3. **if** n <= 1:  
   

4.     **return** False  
   

5. **if** n <= 3:  
   

6.     **return** True  
   

7. **if** n % 2 == 0:  
   

8.     **return** False  
   

10. r, s = 0, n - 1  
    

11. **while** s % 2 == 0:  
    

12.     r += 1  
    

13.     s //= 2  
    

15. **for** _ **in** range(k):  
    

16.     a = random.randint(2, n - 1)  
    

17.     x = pow(a, s, n)  
    

18.     **if** x == 1 **or** x == n - 1:  
    

19.         **continue**  
    

21.     **for** _ **in** range(r - 1):  
    

22.         x = pow(x, 2, n)  
    

23.         **if** x == n - 1:  
    

24.             **break**  
    

25.     **else**:  
    

26.         **return** False  
    

28. **return** True  
    

选择与 φ(n) 互质的整数模块 (generate_coprime):
选择小素数作为与 φ(n) 互质的整数 e。
如果没有找到小素数，继续使用随机选择方法。

1. def generate_coprime(phi_n):

2. # 选择小素数作为与 φ(n) 互质的整数 e  
   

3. small_primes = [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97]  
   

5. **for** prime **in** small_primes:  
   

6.     **if** 1 < prime < phi_n **and** gcd(prime, phi_n) == 1:  
   

7.         **return** prime  
   

9. # 如果没有找到小素数，可以继续使用原来的随机选择方法  
   

10. **return** random.choice([i **for** i **in** range(2, phi_n) **if** gcd(i, phi_n) == 1])  
    

求最大公约数模块 (gcd):
使用辗转相除法求两个数的最大公约数。
求模反元素模块 (mod_inverse):

1. def gcd(a, b):

2. **while** b:  
   

3.     a, b = b, a % b  
   

4. **return** a  
   

使用扩展欧几里得算法计算模反元素。

1. def mod_inverse(a, m):

2. # 使用扩展欧几里得算法计算模反元素  
   

3. m0, x0, x1 = m, 0, 1  
   

4. **while** a > 1:  
   

5.     q = a // m  
   

6.     m, a = a % m, m  
   

7.     x0, x1 = x1 - q * x0, x0  
   

8. **return** x1 + m0 **if** x1 < 0 **else** x1  
   

加密模块 (encrypt):

对明文进行加密，将每个字符转换为ASCII码，使用公钥中的 e 进行模幂运算，得到密文。

1. def encrypt(message, public_key):

2. **print**("正在加密")  
   

3. n, e = public_key  
   

4. cipher_text = [pow(ord(char), e, n) **for** char **in** message]  
   

5. **return** cipher_text  
   

解密模块 (decrypt):

1. def decrypt(cipher_text, private_key):

2. n, d = private_key  
   

3. plain_text = ''.join([chr(pow(char, d, n)) **for** char **in** cipher_text])  
   

4. **return** plain_text  
   

六、实验结果及软件使用说明

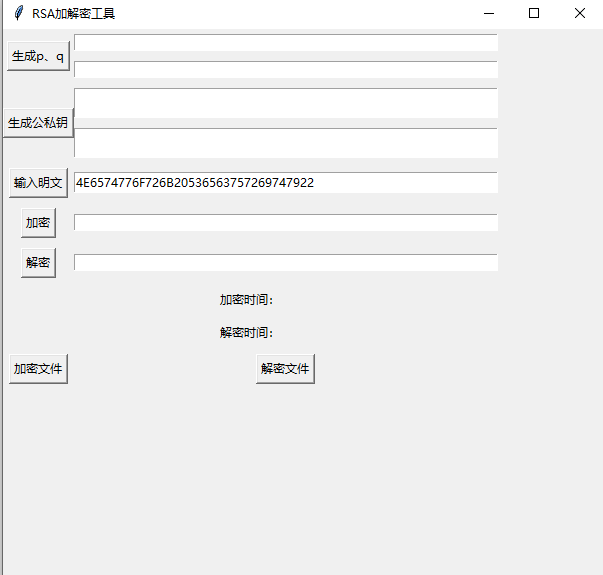
图 2 主界面工具

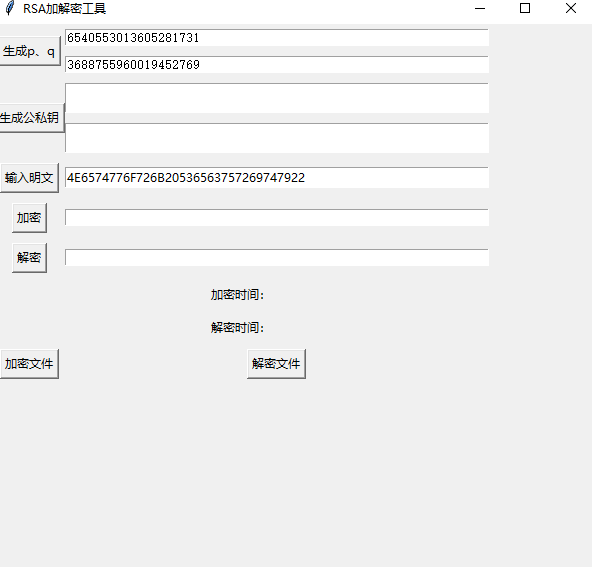
图 3 生成pq

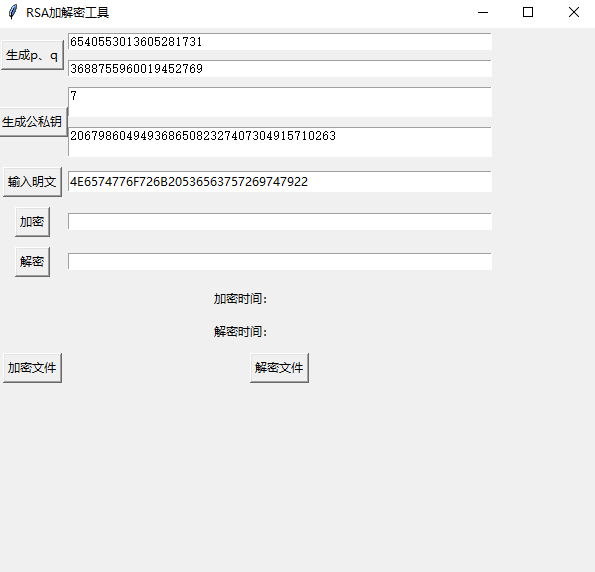
图 4 生成公私钥

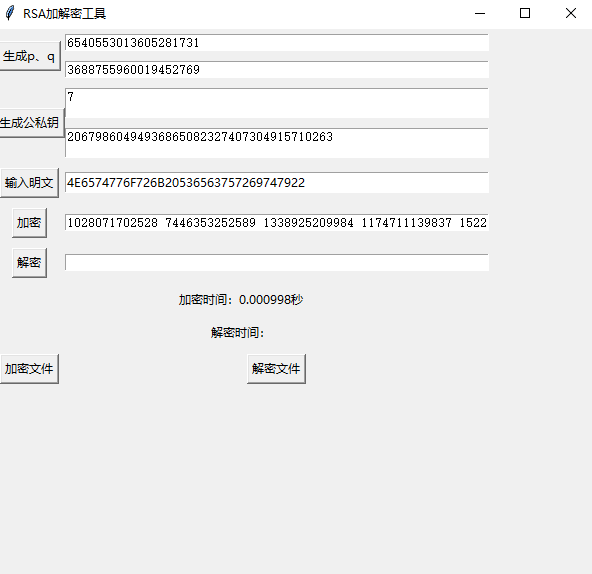
图 5 加密

图 6 解密

图 7 加密文件

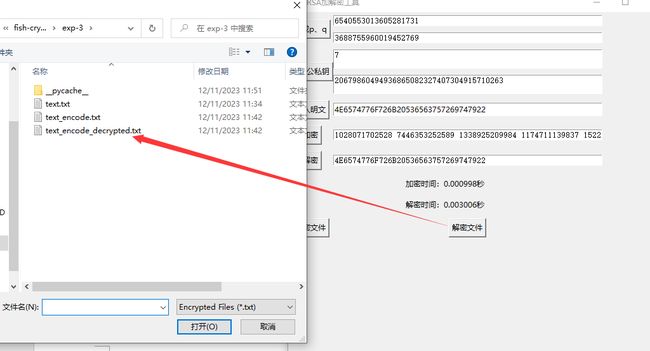
图 8 解密文件

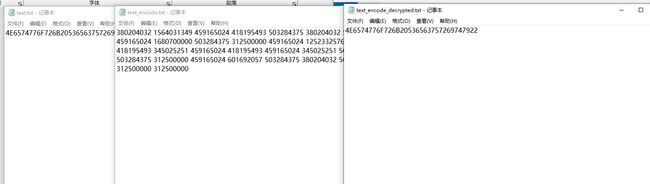
图 9 文件内容

七、源代码

'''
Author: Martin
Date: 2023-11-12 10:50:29
Description: 
'''
import random

def generate_keypair(p,q):

    # 计算 n 和 φ(n)
    n = p * q
    phi_n = (p - 1) * (q - 1)

    # 选择公钥 e，确保 e 和 φ(n) 互质
    print("正在生成公钥 e")
    e = generate_coprime(phi_n)

    # 计算私钥 d，使得 (e * d) % φ(n) = 1
    print("正在计算私钥 d")
    d = mod_inverse(e, phi_n)

    return ((n, e), (n, d))

def generate_large_prime():
    while True:
        num = random.getrandbits(64)
        if is_prime(num):
            return num

def is_prime(n, k=5):
    # Miller-Rabin 素性测试，可根据需要调整参数 k
    if n <= 1:
        return False
    if n <= 3:
        return True
    if n % 2 == 0:
        return False

    r, s = 0, n - 1
    while s % 2 == 0:
        r += 1
        s //= 2

    for _ in range(k):
        a = random.randint(2, n - 1)
        x = pow(a, s, n)
        if x == 1 or x == n - 1:
            continue

        for _ in range(r - 1):
            x = pow(x, 2, n)
            if x == n - 1:
                break
        else:
            return False

    return True

def generate_coprime(phi_n):
    # 选择小素数作为与 φ(n) 互质的整数 e
    small_primes = [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97]
    
    for prime in small_primes:
        if 1 < prime < phi_n and gcd(prime, phi_n) == 1:
            return prime
    
    # 如果没有找到小素数，可以继续使用原来的随机选择方法
    return random.choice([i for i in range(2, phi_n) if gcd(i, phi_n) == 1])

def gcd(a, b):
    while b:
        a, b = b, a % b
    return a

def mod_inverse(a, m):
    # 使用扩展欧几里得算法计算模反元素
    m0, x0, x1 = m, 0, 1
    while a > 1:
        q = a // m
        m, a = a % m, m
        x0, x1 = x1 - q * x0, x0
    return x1 + m0 if x1 < 0 else x1

def encrypt(message, public_key):
    print("正在加密")
    n, e = public_key
    cipher_text = [pow(ord(char), e, n) for char in message]
    return cipher_text

def decrypt(cipher_text, private_key):
    n, d = private_key
    plain_text = ''.join([chr(pow(char, d, n)) for char in cipher_text])
    return plain_text

if __name__ == "__main__":

    p = generate_large_prime()
    q = generate_large_prime()

    # 生成公私钥对
    public_key, private_key = generate_keypair(p,q)

    # 待加密的文本
    plaintext = "4E6574776F726B20536563757269747922"


    # 加密
    cipher_text = encrypt(plaintext, public_key)
    print(f"Ciphertext: {cipher_text}")
    print(type(cipher_text[0]))
    # 解密
    decrypted_text = decrypt(cipher_text, private_key)
    print(f"Decrypted Text: {decrypted_text}")

import tkinter as tk
from cryptography.hazmat.primitives import serialization
from cryptography.hazmat.primitives.asymmetric import rsa, padding
import time
import rsa
from tkinter import filedialog

class RSAApp:
    def __init__(self, master):
        self.master = master
        master.title("RSA加解密工具")
        master.geometry("600x550")

        # 生成 p、q 按钮
        self.generate_pq_button = tk.Button(master, text="生成p、q", command=self.generate_pq)
        self.generate_pq_button.grid(row=0, column=0, pady=5,rowspan=2)

        # 生成 p、q 结果显示文本框
        self.p_output_text = tk.Text(master, height=1, width=60)
        self.p_output_text.grid(row=0, column=1, pady=5)

        self.q_output_text = tk.Text(master, height=1, width=60)
        self.q_output_text.grid(row=1, column=1, pady=5)

        # 生成公钥、私钥按钮
        self.generate_keys_button = tk.Button(master, text="生成公私钥", command=self.generate_keys)
        self.generate_keys_button.grid(row=2, column=0, pady=5,rowspan=2)

        # 生成公钥、私钥结果显示文本框
        self.e_output_text = tk.Text(master, height=2, width=60)
        self.e_output_text.grid(row=2, column=1, pady=5)
        self.d_output_text = tk.Text(master, height=2, width=60)
        self.d_output_text.grid(row=3, column=1, pady=5)

        # 明文输入按钮 美观
        self.input_button = tk.Button(master, text="输入明文")
        self.input_button.grid(row=4, column=0, pady=5)

        # 明文输入框
        self.plaintext_entry = tk.Entry(master, width=60)
        self.plaintext_entry.grid(row=4, column=1, columnspan=3, pady=5)
        self.plaintext_entry.insert(tk.END, "4E6574776F726B20536563757269747922")

        # 加密按钮
        self.encrypt_button = tk.Button(master, text="加密", command=self.encrypt)
        self.encrypt_button.grid(row=5, column=0, pady=5)

        # 密文输出文本框
        self.encrypt_output_text = tk.Text(master, height=1, width=60)
        self.encrypt_output_text.grid(row=5, column=1, pady=5)

        # 解密按钮
        self.decrypt_button = tk.Button(master, text="解密", command=self.decrypt)
        self.decrypt_button.grid(row=6, column=0, pady=5)

        # 解密输出文本框
        self.decrypt_output_text = tk.Text(master, height=1, width=60)
        self.decrypt_output_text.grid(row=6, column=1, pady=5)

        # 显示时间的Label
        self.encrypt_time_label = tk.Label(master, text="加密时间：")
        self.encrypt_time_label.grid(row=7, column=0, columnspan=2, pady=5)

        self.decrypt_time_label = tk.Label(master, text="解密时间：")
        self.decrypt_time_label.grid(row=8, column=0, columnspan=2, pady=5)

         # 导入加密文件按钮
        self.import_encrypted_button = tk.Button(master, text="加密文件", command=self.import_encrypted_file)
        self.import_encrypted_button.grid(row=9, column=0, pady=5)

        # 解密文件按钮
        self.decrypt_button = tk.Button(master, text="解密文件", command=self.decrypt_file)
        self.decrypt_button.grid(row=9, column=1, pady=5)


    def generate_pq(self):
        # 实现生成p、q的逻辑
        # 更新文本框显示生成的p、q
        self.p = rsa.generate_large_prime()
        self.q = rsa.generate_large_prime()
        self.p_output_text.delete("1.0", tk.END)
        self.p_output_text.insert(tk.END, self.p)
        self.q_output_text.delete("1.0", tk.END)
        self.q_output_text.insert(tk.END, self.q)

    def generate_keys(self):
        # 实现生成公私钥的逻辑
        # 更新文本框显示生成的公私钥
        self.public_key, self.private_key = rsa.generate_keypair(self.p,self.q)
        self.n, self.e = self.public_key
        self.n, self.d = self.private_key
        self.e_output_text.delete("1.0", tk.END)
        self.e_output_text.insert(tk.END, self.e)
        self.d_output_text.delete("1.0", tk.END)
        self.d_output_text.insert(tk.END, self.d)

    def encrypt(self):
        # 记录加密开始时间
        start_time = time.time()

        # 实现加密的逻辑
        plaintext = self.plaintext_entry.get()
        cipher_text = rsa.encrypt(plaintext, self.public_key)
        self.encrypt_output_text.delete("1.0", tk.END)
        self.encrypt_output_text.insert(tk.END, cipher_text)
        print(f"Ciphertext: {cipher_text}")
        # 记录加密结束时间
        end_time = time.time()
        elapsed_time = end_time - start_time
        self.encrypt_time_label.config(text=f"加密时间：{elapsed_time:.6f}秒")

    def decrypt(self):
        # 记录解密开始时间
        start_time = time.time()
        # 实现解密的逻辑
        # 获取密文输出文本框的值
        cipher_text = self.encrypt_output_text.get("1.0", tk.END).strip()

        print(f"###plaintext{cipher_text}")
        cipher_list = list(map(int, cipher_text.split()))
        print(f"###plaintext{cipher_list}")
        print(f"###type - plaintext{type(cipher_list)}")

        cipher_text = rsa.decrypt(cipher_list, self.private_key)
        self.decrypt_output_text.delete("1.0", tk.END)
        self.decrypt_output_text.insert(tk.END, cipher_text)
        print(f"Ciphertext: {cipher_text}")
        # 记录解密结束时间
        end_time = time.time()
        elapsed_time = end_time - start_time
        self.decrypt_time_label.config(text=f"解密时间：{elapsed_time:.6f}秒")


    def encrypt_file(self, file_path):
        # 读取文件内容
        with open(file_path, 'r') as file:
            data = file.read()

        # 记录加密开始时间
        start_time = time.time()
        print("data:"+data)
        # 使用RSA加密
        encrypted_data = rsa.encrypt(data, self.public_key)

        # 记录加密结束时间
        end_time = time.time()
        elapsed_time = end_time - start_time
        print(f"加密时间：{elapsed_time:.6f}秒")

        # 保存加密后的文件
        encrypted_file_path = file_path[:-4] + "_encode.txt"
        with open(encrypted_file_path, 'w') as file:
            file.write(' '.join(map(str, encrypted_data)))


        print(f"文件成功加密，保存为：{encrypted_file_path}")

    def import_encrypted_file(self):
        # 选择加密文件
        file_path = filedialog.askopenfilename(title="选择加密文件", filetypes=[("Encrypted Files", "*.txt")])
        if file_path:
            self.encrypt_file(file_path)

    def decrypt_file(self):
        # 选择待解密的文件
        file_path = filedialog.askopenfilename(title="选择待解密文件", filetypes=[("Encrypted Files", "*.txt")])
        if file_path:
            # 记录解密开始时间
            start_time = time.time()

            # 读取加密文件内容
            with open(file_path, 'r') as file:
                encrypted_data = file.read()

            cipher_list = list(map(int, encrypted_data.split()))

            # 使用RSA解密
            decrypted_data = rsa.decrypt(cipher_list, self.private_key)

            # 记录解密结束时间
            end_time = time.time()
            elapsed_time = end_time - start_time
            print(f"解密时间：{elapsed_time:.6f}秒")

            # 保存解密后的文件
            decrypted_file_path = file_path[:-4] + "_decrypted.txt"
            with open(decrypted_file_path, 'w') as file:
                file.write(decrypted_data)

            print(f"文件成功解密，保存为：{decrypted_file_path}")


if __name__ == "__main__":
    root = tk.Tk()
    app = RSAApp(root)
    root.mainloop()