4、以时间序列为特征

用滞后嵌入法预测过去的未来。

1、什么是序列依赖性？

在早期的课程中，我们研究了时间序列的一些属性，这些属性最容易被建模为时间依赖性属性，也就是说，我们可以直接从时间索引中得到特征。然而，有些时间序列的属性只能被建模为序列依赖性属性，也就是说，使用目标序列的过去值作为特征。这些时间序列的结构可能从时间图中并不明显；然而，与过去的值相比，结构变得清晰——正如我们在下面的图中看到的那样。

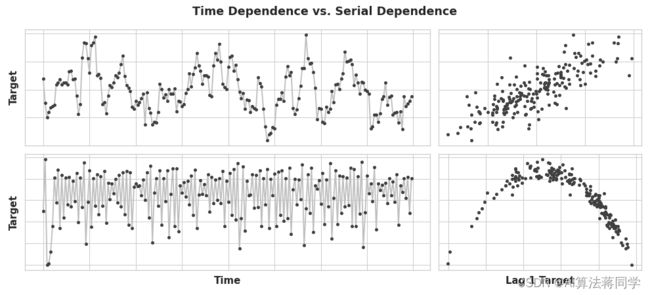
这两个序列具有序列依赖性，但没有时间依赖性。右边的点的坐标是(t-1时的值, t时的值)。

对于趋势和季节性，我们训练模型来拟合像上图左边那样的曲线——模型正在学习时间依赖性。这节课的目标是训练模型来拟合像右边那样的曲线——我们希望它们学习序列依赖性。

1.1周期性

序列依赖性表现的一种特别常见的方式是周期性。周期性是时间序列中增长和衰退的模式，这与序列在某一时间的值如何依赖于前一时间的值有关，但不一定与时间步本身有关。周期性行为是那些可以影响自身或其反应持续一段时间的系统的特征。经济、疫情、动物种群、火山爆发和类似的自然现象通常会显示出周期性行为。

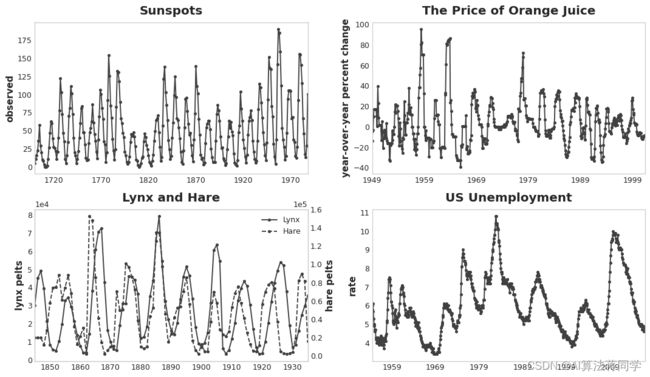
四个具有周期性行为的时间序列。

区分周期性行为和季节性的是，周期并不一定与时间有关，就像季节一样。周期中发生的事情与发生的特定日期关系不大，更多的是与最近过去发生的事情有关。至少相对独立于时间意味着周期性行为可以比季节性更不规则。

2、延迟序列和延迟图

为了研究时间序列中可能存在的序列依赖性（如周期性），我们需要创建序列的"延迟"副本。延迟一个时间序列意味着将其值向前移动一个或多个时间步，或者等效地，将其索引中的时间向后移动一个或多个步骤。无论哪种情况，效果都是延迟序列中的观察值将看起来发生在较晚的时间。

这显示了美国的月度失业率(y)以及其第一和第二延迟序列(y_lag_1和y_lag_2)。注意延迟序列的值是如何向前移动的。

In [1]:

import pandas as pd

# Federal Reserve dataset: https://www.kaggle.com/federalreserve/interest-rates
reserve = pd.read_csv(
    "../input/ts-course-data/reserve.csv",
    parse_dates={
   'Date': ['Year', 'Month', 'Day']},
    index_col='Date',
)

y = reserve.loc[:, 'Unemployment Rate'].dropna().to_period('M')
df = pd.DataFrame({
   
    'y': y,
    'y_lag_1': y.shift(1),
    'y_lag_2': y.shift(2),    
})

df.head()

Out[1]:

	y	y_lag_1	y_lag_2
Date
1954-07	5.8	NaN	NaN
1954-08	6.0	5.8	NaN
1954-09	6.1	6.0	5.8
1954-10	5.7	6.1	6.0
1954-11	5.3	5.7	6.1

通过延迟一个时间序列，我们可以使其过去的值看起来与我们试图预测的值同时发生（换句话说，它们在同一行）。这使得延迟序列作为建模序列依赖性的特征非常有用。为了预测美国的失业率序列，我们可以使用y_lag_1和y_lag_2作为特征来预测目标y。这将把未来的失业率预测为前两个月失业率的函数。

2.1延迟图

时间序列的延迟图显示了其值与其延迟的关系。通过查看延迟图，时间序列的序列依赖性通常会变得明显。从美国失业率的延迟图中，我们可以看到当前失业率与过去的失业率之间存在强烈且明显的线性关系。

美国失业率的延迟图，标出了自相关性。

衡量序列依赖性的最常用指标被称为自相关性，它只是时间序列与其延迟的相关性。例如，美国失业率在延迟1时的自相关性为0.99，在延迟2时为0.98，依此类推。

2.2选择延迟

在选择用作特征的延迟时，通常不会有必要包括每一个具有大自相关性的延迟。例如，在美国失业率中，延迟2的自相关性可能完全来自于延迟1的"衰减"信息——只是从前一步传递过来的相关性。如果延迟2没有包含任何新的信息，那么如果我们已经有了延迟1，就没有理由再包括它。

偏自相关性告诉你一个延迟在考虑了所有前面的延迟后的相关性——也就是说，这个延迟所贡献的"新"相关性。绘制偏自相关图可以帮助你选择哪些延迟特征。在下面的图中，延迟1到延迟6都超出了"无相关性"的区间（蓝色），所以我们可能会选择延迟1到延迟6作为美国失业率的特征。（延迟11可能是假阳性。）

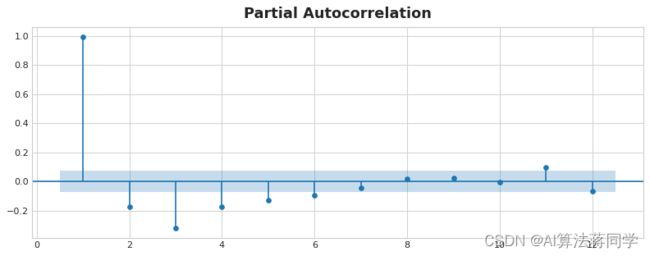
美国失业率的偏自相关性，通过延迟12，有95%的置信区间无相关性。

像上面那样的图被称为相关图。对于延迟特征来说，相关图本质上就是傅里叶特征的周期图。

最后，我们需要注意，自相关性和偏自相关性都是线性依赖性的度量。因为现实世界的时间序列通常具有大量的非线性依赖性，所以在选择延迟特征时，最好是查看延迟图（或者使用一些更一般的依赖性度量，比如互信息）。太阳黑子序列具有我们可能会忽视的非线性依赖性的延迟。

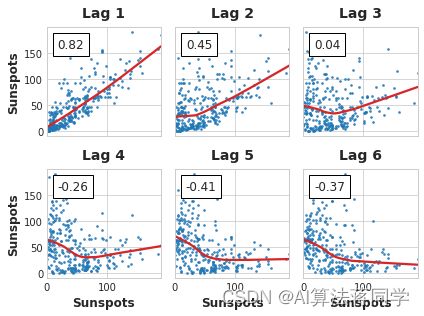
太阳黑子序列的延迟图。

这样的非线性关系可以被转换为线性，或者由适当的算法学习。

3、示例 - 流感趋势

流感趋势数据集包含了2009年至2016年间每周的流感就诊记录。我们的目标是预测未来几周的流感病例数量。

我们将采取两种方法。首先，我们将使用延迟特征来预测就诊人数。其次，我们将使用另一组时间序列的延迟来预测就诊人数：由Google Trends捕获的与流感相关的搜索词。

In [2]:

from pathlib import Path
from warnings import simplefilter

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
from scipy.signal import periodogram
from sklearn.linear_model import