论文阅读：Interactive Multiobjective Optimization：A Review of the State-of-the-Art

Interactive Multiobjective Optimization：A Review of the State-of-the-Art

作者：Bin Xin、Lu Chen、Jie Chen

期刊：IEEE Access 、2018

DOI：10.1109/AXXESS.2018.2856832

---

摘要

交互式多目标优化 (IMO) 旨在通过决策者 DM 逐步提供的偏好信息找到决策者最喜欢的解决方案。在此过程中，决策者可以调整他/她的偏好，只探索搜索空间中感兴趣的区域。近几十年来，IMO逐渐成为多标准决策（MCDM）和进化多目标优化（EMO）两个不同社区的共同兴趣。 MCDM 社区开发的 IMO 方法通常使用数学规划方法 MP 来搜索单个首选的帕累托最优解，而植根于 EMO 的方法通常使用进化算法 EAs 在决策者的首选区域中生成一组具有代表性的解决方案。本文旨在从 MCDM 和 EMO 的角度回顾 IMO 的研究。本文考虑到 交互模式、偏好信息、偏好模型 和 搜索引擎/优化算法 四个分类标准，以识别重要的IMO因素并区分各种IMO方法。并根据分类，对最先进的 IMO 方法进行分类和回顾，总结其背后的设计思想。强调和讨论了一系列重要问题，例如决策者的负担、认知偏差和偏好不一致，以及评估 IMO 方法的绩效测量和指标。还提出了几个值得未来研究的有希望的方向。

---

1.Introduction

多目标优化问题的定义如下：
$$\begin{gathered} minimizef(x)=\{f_1(x),f_2(x),\dots ,f_k(x)\} \\ subjecttox\in S\subset R^n \end{gathered}$$
Pareto Dominace
Pareto Optimality
Weak Pareto Optimality

多目标优化的最终目标是支持决策者找到他/她最偏好的解决方案 (MPS)。根据DM参与求解过程的阶段，多目标优化方法可分为以下三类：

1. 先验式方法/A priori methods：DM首先提供他/她的全局偏好信息。然后，找到满足偏好信息的帕累托最优解。这种方法由于计算复杂度低而被广泛使用。然而在现实中，DM 的全局偏好信息通常是未知的，尤其是当他/她对 MOP 知之甚少时。
2. 后验式方法/A posteriori methods：DM 在算法找到的近似帕累托前沿中选择最偏好的一个。后验方法的优点是 DM 可以概览 Pareto 前沿。然而，逼近整个帕累托前沿在计算上是昂贵的。此外，随着目标数量的增加，代表帕累托前沿所需的非支配解决方案的数量呈指数增长 [5]、[6]，这增加了 DM 选择最优选解决方案的负担。
3. 交互式方法/Interactive methods：在交互式多目标优化 (IMO) 方法中，DM 在求解过程中逐步指定偏好，以引导算法搜索到他/她的首选区域。 DM不需要任何全局偏好信息，他/她可以从优化过程中学习并调整偏好。此外，只需要找到DM感兴趣的解决方案中的一个或一小部分，从而降低了计算复杂度并且DM不需要同时比较许多非支配解。总之，交互式方法克服了先验和后验方法的弱点。

多准则决策 MCDM 领域可以划分为两个部分：

1. 在有限备选解集中求解离散问题的多属性决策/multiple attribute decision making

2. 求解连续问题的多目标决策/multiple objective decision making。

后面一段叙述了MCDM的发展过程。

2.IMO方法分类

交互式多目标优化主要包含两个重要的方面：决策者和机器(算法)。整个交互式流程如下：DM 根据他/她对问题的了解和算法提供的解决方案来表达他/她的偏好信息。基于提供的偏好，机器建立一个偏好模型，该模型是偏好信息和搜索引擎之间以及DM和机器之间的桥梁。它的作用是将 DM 的偏好整合到机器中，并引导搜索引擎找到 DM 感兴趣的解决方案。获得的解决方案会显示给DM，以帮助他/她提供新的偏好。通过与机器的交互，DM可以了解问题并调整他/她的偏好以最终找到他/她的MPS。

IMO 的四个重要因素：交互模式、偏好信息、偏好模型、搜索引擎

2.1交互模式Interaction Pattern

IAR：Interaction After a complete Run

  搜索引擎完整运行至结束，并根据决策者最近提供的偏好信息返回期望解决方案。
  像 权衡和目标分类 这样的偏好信息更适用于 IAR 模式，因为在帕累托最优解中考虑权衡才更有意义。

IDR：Interaction During a complete Run

  决策者能够暂停算法的运行，在决策者提供偏好信息后继续运行算法。
  在 IAR 中，DM-Machine 的交互是由机器（算法）触发的，在 IDR 中，DM-Machine 的交互是由决策者主导的。

2.2 偏好信息Preference Information

本文将偏好信息划分为三个类别：期望值/expection、目标函数的比较/the comparison of objective functions、解决方案的比较/the comparison of solutions。

2.2.1 期望值/expection

  期望值常常以参考点的形式来表示决策者想要目标函数达到的期望值。往往需要知道目标函数的取值范围，这需要一些先验知识，也会带来额外的计算成本。

2.2.2 目标函数的比较/the comparison of objective functions

常用的方式有：权重Weight、权衡Tradeoffs、目标的分类the classification of objectives。
  权重反映的是目标函数之间的相对重要关系，常以 k 个权值组成的向量形式表示。一些方法中会要求决策者提供目标函数的相对重要等级，这会降低决策者的负担，但是当目标函数很多时，决策者需要在目标函数之间做多次比较。

  权衡意味着以一种可行的解决方案中通过牺牲一个目标函数来获得另一个目标函数的提升。一种常见的权衡形式是无差异权衡（或边际替代率，Marginal Rate of Sustitution，MRS），它是指一个目标的增量以补偿另一个目标的一个单位减量。权衡能够提供一个精准的搜索方向，从当前帕累托最优解中发现更多满意的解。决策者需要在目标函数之间做出大量权衡。

  目标的分类是根据对目标值的期望变化类型，在当前帕累托最优解中对目标函数进行分类。Miettinen 等人划分了 5 种类型：
   1. $I^{<}$：该分类中的目标函数应该被提升；
   2. $I^{\le }$：该分类中的目标函数应该被提升，直到满足一些期望等级；
   3. $I^{=}$：该分类中的目标函数被接受；
   4. $I^{\ge }$：该分类中的目标函数应该被牺牲，直到某些下界；
   5. $I^{♢}$：该分类中的目标函数可以自由变化。

也可以采用这五类的不同子集。对目标函数进行分类是一种有效表达偏好信息的方法。相比参考点方法，决策者能够更好地控制优化进程。但是该方法可能对决策者带来更多的负担。

2.2.3 解决方案的比较/the comparison of solutions

常用的形式有：解决方案之间的成对比较、解决方案的分类、选择偏好解。

1. 解决方案之间的成对比较判断两个解之间的关系：优于关系Preferred、无法比较incomparable或中立的indifferent。
2. 解决方案的分类是将解决方案划分为不同的集合，每个集合中的解都是无法比较或中立的。
3. 选择偏好解意味着在一个解集中选择最好的解。

作为定性偏好信息，与指定定量偏好（如期望水平和权衡）相比，解决方案的比较对 DM 造成的认知负担相对较少。但是，需要注意的是，随着解决方案数量的增加，DM 的负担也可能会增加。

目标函数的比较和解决方案间的比较都需要决策者在表达偏好时做出比较。两者的不同在于，前者反映的是目标函数之间的关系，后者反映的是目标矢量之间的关系。

2.3 偏好模型Preference Model

常用的偏好模型有：值函数或效用函数 / Value function (utility function)，支配关系 / dominance relation、决策规则 / decision rules。

2.3.1 值函数 Value Function

值函数 (VF) 是定量评估解决方案的所有目标函数的标量函数。其参数由 DM 直接指定或根据 DM 的偏好间接计算。决策者常常以 $U=U(f_1,f_2,\dots ,f_k)$ 的形式提供偏好信息。显式 VF 可以提供目标空间中目标向量的完整排名。它的最佳解决方案是 DM 的 MPS。然而，DM 的 VF 通常不明确，因为 DM 没有关于 MOP 的完整信息。许多方法根据 DM 的偏好动态地对 DM 的基础 VF 建模。下面介绍三种流行的 VF。

1. 加权度量 Weighted Metrics

   加权度量测量目标向量与某个点之间的距离。这个点可以是理想点 an ideal point、最低点 a nadir point等。权值能反映决策者的偏好信息。常用的加权度量是L范式$$L_p-norms,p\in [1,\infty )$$

2. 成就标量函数Achievement Scalarizing Functin
     成就标量函数 (ASF) 被视作一种改进的 VF，既表达了实现愿望水平的效用，也表达了不实现愿望水平的不利影响 。迄今为止，已开发出多种形式的 ASF。常用的两种形式如下：
   

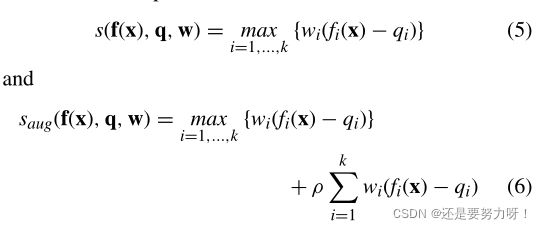
   交互式 MCDM 方法通常使用 ASFs 来表达最小化问题。交互式EMO方法常使用 ASFs 将种群划分为多个前沿。

3. 附加值函数 Additive VF

   附加值函数的常用形式如下：$U(f(x))={\sum }_{i=1}^k{u}_i(f_i(x))$，其中，$u_i(\cdot )$ 是非递减边际值函数 non-decreasing marginal VFs。
   VFs的其他形式有：多项式函数和高斯函数。

对于加权度量、ASF 和高斯函数等 VF，其权重、参考点和中心向量等参数由 DM 在每次迭代时直接指定。附加 VF 和多项式 VF 可以从 DM 的先前和当前偏好中学习。一些 IMO 方法不对 DM 的基础 VF 的形式做出任何先验假设，而是使用神经网络和支持向量机等技术从他/她的偏好中学习 VF 。

2.3.2 支配关系 Dominance Relation

支配关系以一对解决方案的关系来描述 DM 的偏好。在交互式 MOEA 的选择算子中，它经常被用来代替 Pareto 支配关系。支配关系主要包含：优于/支配关系Preferred、无法比较incomparable或中立的indifferent。

许多支配关系将帕累托支配关系与 DM 的偏好结合起来，因此也可以比较非支配解。许多学者在帕累托支配关系的基础上提出了新的支配关系。

2.3.3 决策规则 / decision rules

决策规则将 DM 的偏好建模为一组 “IF-THEN” 规则。通常，决策规则的前提部分指定了目标和/或解决方案应满足的条件。决策部分指定解决方案之间的关系或为其分配分数。

如果目标和/或解决方案满足某些条件，则决策规则可以指定解决方案之间的关系或分配解决方案的得分以促进首选解决方案的选择。决策规则形式的偏好模型比经典的功能模型或关系模型更通用，并且由于其自然语法，DM更易于理解。具体来说，作为一种决策规则，模糊规则可以处理 DM 的定性偏好，并将其转化为目标或解决方案的定量信息。

2.3.4 混合偏好模型

2.4搜索引擎 Search Engine、

搜索引擎基于偏好模型，搜索 DM 感兴趣的解决方案。即使在 IMO 中有人参与，搜索引擎仍然是解决问题性能的决定性因素。如何选择或设计一个称职的搜索引擎一直是 IMO 的一个基本而关键的问题，尤其是在解决难以优化的问题时。

我们将 IMO 方法中使用的搜索引擎分为：数学规划 MP 技术 和非数学规划 non-MP 技术。

针对线性规划、非线性规划和多目标规划等不同的 MP 分支，已经开发了各种成熟的优化技术来解决相应的问题，例如线性规划问题的单纯形法和非线性问题的顺序二次规划。MCDM 社区开发的 IMO 方法通常采用 MP 技术来生成 Pareto 最优解。

非 MP 技术主要是启发式方法，包括 EAs、禁忌搜索、模拟退火等。

• EAs 强调通用性，在解决多模态、不连续、强约束和动态问题等复杂 SOPs 中显示出优势。 EAs 具有基于群体的搜索范式，有助于在解决方案空间中进行全局搜索以及并行实施。与 MP 技术相比，EAs 可能会比较耗时，并且不能保证找到 SOPs 的最优解。然而，他们能够解决 MP 技术难以或不可能解决的复杂 SOPs。此外，EAs 能够在单次运行中找到 MOPs 的一组（近似）帕累托最优解，这在多目标优化（后验或交互方法）中非常有吸引力，因为 DM 可以获得更多信息并有更多的选择。

• 群体智能 Swarm Intelligence/SI ：一群简单的个体通过相互之间以及与环境的交互来表现出整体的智能行为。典型的基于SI的优化算法包括蚁群优化 Ant Colony Optimization 、粒子群优化 Particle Swarm Opyimization 、人工免疫系统 Artificial Immune System 、蜂群优化 bee colony optimization 、鱼群搜索 fish school search 、烟花算法 fireworks algorithm、脑风暴优化 brain storm optimization等。

• 许多研究开始将 EAs 和局部搜索相结合的模因算法 Memetic algorithm 。最近还研究了将 MOEA 与局部搜索方法杂交的模因 MOEA。包含有针对性的局部搜索可以提高 MOEA 的整体性能。

---

以上内容是该文献对交互式多目标优化的发展历程、文献分类标准进行了介绍，后续内容主要是关于分类的介绍，以及每个分类下典型论文的介绍。