【经典案例 | 骑士之旅】回溯算法解决经典国际象棋骑士之旅问题 | 详解Knight’s Tour Problem数学问题

骑士之旅问题

by.Qin3Yu

请注意，阅读本文需要您先掌握顺序表的基本操作，具体可参阅我的往期博客：
【C++数据结构 | 顺序表速通】使用顺序表完成简单的成绩管理系统.by.Qin3Yu

本文所使用搜索方法实质为深度优先搜索(DFS)，相关内容可参阅我的往期博客：
【算法详解 | DFS算法】深度优先搜索解走迷宫问题 | 深度优先图遍历.by.Qin3Yu

文中所有代码使用 C++ 举例，且默认已使用 std 命名空间：

using namespace std;

针对本文中的部分代码案例，还需要额外导入以下头文件：

#include 

---

题目速览

• 骑士之旅（Knight’s Tour Problem） 是一个非常经典的棋盘问题，该问题要求在一个国际象棋棋盘上，以象棋中骑士的移动方式来将棋盘上的所有方格均遍历一遍，且每个方格只能经过一次。
• 这个问题在数学领域被研究为一种组合优化问题，考验着人们的思维和解题能力。有关骑士之旅问题的研究始于18世纪，但至今仍然备受数学爱好者关注。

注：骑士（也称为马）的移动规则为走L形，即横向或纵向移动2格，再竖向或横向移动1格。

---

算法详解

• 骑士之旅问题是个复杂的组合优化问题，如果用传统的数学方法解决，需要经历大量的建模与计算，但是得益于现代计算机的强大算力，我们可以用最直接的回溯方法解决此问题。
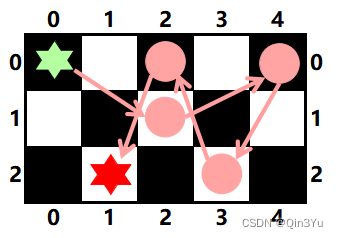
• 具体而言，我们把所有可能的方法全部尝试一遍，直到尝试出正确结果或者得出不可能的结论。如下图的棋盘所示，我们先根据固定的规则走出n步，直到如图所示：

• 此时，我们的骑士（红色多边形表示）已经没有合法的格子可以走，则我们开始回溯路径，即返回至上n步，直到还有其他可以走的且未走过的路径为止，再进行正常的移动：

• 思路其实非常简单，即 暴力 + 回溯 的思想即可。

---

代码实现

• 首先，定义出棋盘和路径，国际象棋的棋盘为8x8规格的二维图，因此，我们 用二维数组来表示棋盘 ，我们使用8x8的二维数组，并且将其初始化为 -1 ，表示此格子还没有被访问过，然后我们还要定义出骑士的移动路径，我们可以用一个 包含二位坐标对 (pair) 的数组来表示移动路径 ，且将它的长度定义为8x8：

// 定义棋盘大小为8
#define N 8
...

// 定义棋盘规格为8x8，且初始化为未访问（-1）
vector<vector<int>> board(N, vector<int>(N, -1));

// 用pair定义骑士的移动路径，即（x,y）
vector<pair<int, int>> path(N * N);

• 第二步，我们需要告诉计算机骑士的移动规则，我们在上文使用了二维数组来定义棋盘，那我们也可以用两个数组来表示骑士的移动规则，如代码所示，一对 （dx,dy） 坐标则表示一个可移动的位置：

int dx[8] = { -2, -1, 1, 2, 2, 1, -1, -2 };
int dy[8] = { 1, 2, 2, 1, -1, -2, -2, -1 };

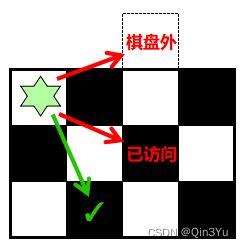
• 接下来，我们还需要定义一个 isSafe 函数来判断骑士将要移动的格子是否已经被访问过或者在棋盘外，具体规则为如果目标格子的坐标值在8x8范围内，且没有被访问过(-1)，则可以移动：

bool isSafe(const vector<vector<int>>& board, int x, int y) {
    return (x >= 0 && x < N && y >= 0 && y < N && board[x][y] == -1);
}

• 最后，我们再设置一个起始点（0,0），并将其标记为已访问且添加至路径中：

// 设置起始位置(0,0)
int startX = 0;
int startY = 0;

// 将起始位置标记为已访问
board[startX][startY] = 0;

//向路径中添加一个坐标pair
path[0] = make_pair(startX, startY);

• 现在便是骑士之旅问题的核心算法，我们需要向函数传入棋盘、路径、起始位置（x 和 y）、移动步数（初始为1）四个参数：

// 为方便阅读写为两行
bool solveKnightTour(vector<vector<int>>& board, 
    vector<pair<int, int>>& path, int x, int y, int moveNum) {}

• 在算法中，我们依次尝试往骑士的八个可移动方向移动，如果可以移动，则移动后再次调用函数（递归），直到移动的步数 moveNum 等于棋盘的格子数 N × N ，则说明骑士已经走遍了整个棋盘，返回 true 。

• 如果8个方向均已被尝试如果8个方向均已被尝试过，那么说明当前路径不能找到一条成功的路径，需要进行回溯操作。回溯操作会将当前位置标记为未访问，然后进入下一个循环，尝试下一个可能的移动方向。

• 具体来说，在这段代码中，如果所有的八个方向都被尝试过后，递归调用 solveKnightTour 函数没有返回 true ，那么程序会执行下面的回溯操作：

1. 将当前位置 (nextX, nextY) 标记为未访问，即 board[nextX][nextY] = -1 。
2. 继续循环，尝试下一个移动方向，即下一个 k 值。
3. 如果所有的方向都被尝试过并且没有找到成功的路径，那么最终 solveKnightTour 函数会返回 false 。

• 这样，程序会回溯到之前的状态，尝试其他的路径。通过不断地回溯和尝试，直到找到一条成功的路径或者所有可能的路径都被尝试过。

// 如果所有方格都已访问，则问题解决
    if (moveNum == N * N)
        return true;

    // 尝试骑士的所有移动方向
    for (int k = 0; k < 8; ++k) {
        int nextX = x + dx[k];
        int nextY = y + dy[k];

        if (isSafe(board, nextX, nextY)) {
            board[nextX][nextY] = moveNum; // 标记该位置为已访问
            path[moveNum] = make_pair(nextX, nextY); // 记录路径

            if (solveKnightTour(board, path, nextX, nextY, moveNum + 1)) 
                return true;

            board[nextX][nextY] = -1; // 回溯，将该位置标记为未访问
        }
    }

    return false;

• 最后我们再打印出最终的路径，即依次遍历并打印出 path 数组中的内容即可：

// 打印解决方案
void printSolution(const vector<pair<int, int>>& path) {
    for (int i = 0; i < N * N; ++i) {

        // 打印出pair中的元素
        cout << "(" << path[i].first << ", " << path[i].second << ") ";

        // 每打印几个便换一行，方便观察
        if ((i + 1) % N == 0) 
            cout << endl;
    }
}

int main() {
    ......

    // 解决骑士之旅问题
    if (solveKnightTour(board, path, startX, startY, 1)) {
        cout << "存在解决方案：" << endl;

        // 调用函数打印
        printSolution(path);
    }
    else
        cout << "不存在解决方案。" << endl;
}

至此，骑士之旅问题的所有内容讲解完毕（=

---

完整代码

参考代码（以8x8棋盘为例）：

#include 
#include 
using namespace std;

// 定义棋盘大小
#define N 8

// 定义骑士的移动方向
int dx[8] = { -2, -1, 1, 2, 2, 1, -1, -2 };
int dy[8] = { 1, 2, 2, 1, -1, -2, -2, -1 };

// 打印解决方案
void printSolution(const vector<pair<int, int>>& path) {
    for (int i = 0; i < N * N; ++i) {
        cout << "(" << path[i].first << ", " << path[i].second << ") ";
        if ((i + 1) % N == 0) 
            cout << endl;
    }
}

// 检查位置是否在棋盘内且尚未访问过
bool isSafe(const vector<vector<int>>& board, int x, int y) {
    return (x >= 0 && x < N && y >= 0 && y < N && board[x][y] == -1);
}

// 使用回溯递归解决骑士之旅问题
bool solveKnightTour(vector<vector<int>>& board, vector<pair<int, int>>& path, int x, int y, int moveNum) {
    // 如果所有方格都已访问，则问题解决
    if (moveNum == N * N)
        return true;

    // 尝试骑士的所有移动方向
    for (int k = 0; k < 8; ++k) {
        int nextX = x + dx[k];
        int nextY = y + dy[k];

        if (isSafe(board, nextX, nextY)) {
            board[nextX][nextY] = moveNum; // 标记该位置为已访问
            path[moveNum] = make_pair(nextX, nextY); // 记录路径

            if (solveKnightTour(board, path, nextX, nextY, moveNum + 1)) 
                return true;

            board[nextX][nextY] = -1; // 回溯，将该位置标记为未访问
        }
    }

    return false;
}

int main() {
    // 初始化棋盘和路径
    vector<vector<int>> board(N, vector<int>(N, -1));
    vector<pair<int, int>> path(N * N);

    // 设置起始位置
    int startX = 0;
    int startY = 0;

    // 将起始位置标记为已访问
    board[startX][startY] = 0;
    path[0] = make_pair(startX, startY);

    // 解决骑士之旅问题
    if (solveKnightTour(board, path, startX, startY, 1)) {
        cout << "存在解决方案：" << endl;
        printSolution(path);
    }
    else
        cout << "不存在解决方案。" << endl;

    system("pause");
    return 0;
}

参考输出：

存在解决方案：
(0, 0) (1, 2) (0, 4) (1, 6) (3, 7) (5, 6) (7, 7) (6, 5)
(4, 6) (2, 7) (3, 5) (4, 7) (6, 6) (7, 4) (5, 5) (3, 6)
(1, 7) (2, 5) (0, 6) (1, 4) (2, 6) (0, 7) (1, 5) (3, 4)
(5, 3) (4, 5) (5, 7) (7, 6) (6, 4) (7, 2) (6, 0) (4, 1)
(2, 2) (0, 3) (2, 4) (0, 5) (1, 3) (0, 1) (2, 0) (3, 2)
(4, 4) (6, 3) (7, 1) (5, 0) (4, 2) (2, 3) (1, 1) (3, 0)
(5, 1) (7, 0) (6, 2) (4, 3) (3, 1) (1, 0) (0, 2) (2, 1)
(3, 3) (5, 2) (4, 0) (6, 1) (7, 3) (5, 4) (7, 5) (6, 7)

---

感谢您的阅读（=

CSDN.by.Qin3Yu