代码随想录算法训练营第十三天 | 104.二叉树的最大深度、559.N叉树的最大深度、111.二叉树的最小深度、222.完全二叉树的节点个数
代码随想录算法训练营第十三天 | 104.二叉树的最大深度、559.N叉树的最大深度、111.二叉树的最小深度、222.完全二叉树的节点个数
文章目录
- 代码随想录算法训练营第十三天 | 104.二叉树的最大深度、559.N叉树的最大深度、111.二叉树的最小深度、222.完全二叉树的节点个数
-
- 1 LeetCode 104.二叉树的最大深度
- 2 LeetCode 559.N叉树的最大深度
- 3 LeetCode 111.二叉树的最小深度
- 4 LeetCode 222.完全二叉树的节点个数
-
- 4.1 普通遍历
- 4.2 利用完全二叉树的特性优化遍历
1 LeetCode 104.二叉树的最大深度
题目链接:https://leetcode.cn/problems/maximum-depth-of-binary-tree/description/
给定一个二叉树
root,返回其最大深度。二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。
示例 1:
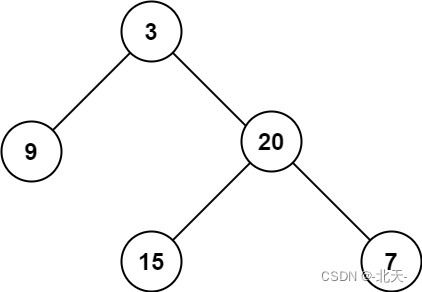
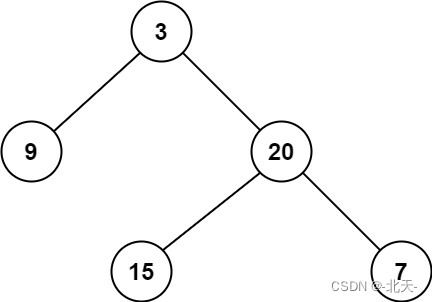
输入:root = [3,9,20,null,null,15,7] 输出:3示例 2:
输入:root = [1,null,2] 输出:2提示:
- 树中节点的数量在
[0, 104]区间内。-100 <= Node.val <= 100
这道题目其实也就是求二叉树的高度,这种类型的题目408考试也可能会出,需要注意一下,这道题目我们就考虑用递归法做,那么前序遍历和后序遍历都可以实现。
首先后序遍历的代码很简单。
(1)Python版本代码
# 后序遍历
class Solution:
def maxDepth(self, root: Optional[TreeNode]) -> int:
if not root:
return 0
L = self.maxDepth(root.left)
R = self.maxDepth(root.right)
if L > R:
return L + 1
else:
return R + 1
我们只需要记录最高的一棵子树,然后加上根节点,就可以知道整颗二叉树的最大高度(深度)。
下面是前序遍历,我们需要额外的定义一个函数,用于递归传参。
# 前序遍历
class Solution:
def maxDepth(self, root: Optional[TreeNode]) -> int:
return self.getHeight(root, 0)
def getHeight(self, root, cur_depth):
if not root:
return cur_depth
L = self.getHeight(root.left, cur_depth + 1)
R = self.getHeight(root.right, cur_depth + 1)
return max(L, R)
(2)C++版本代码
// 后序遍历
class Solution {
public:
int maxDepth(TreeNode* root) {
if (!root) {
return 0;
}
int L = maxDepth(root->left);
int R = maxDepth(root->right);
return std::max(L, R) + 1;
}
};
// 前序遍历
class Solution {
public:
int maxDepth(TreeNode* root) {
return getHeight(root, 0);
}
int getHeight(TreeNode* root, int cur_depth) {
if (!root) {
return cur_depth;
}
int L = getHeight(root->left, cur_depth + 1);
int R = getHeight(root->right, cur_depth + 1);
return std::max(L, R);
}
};
2 LeetCode 559.N叉树的最大深度
题目链接:https://leetcode.cn/problems/maximum-depth-of-n-ary-tree/description/
给定一个 N 叉树,找到其最大深度。
最大深度是指从根节点到最远叶子节点的最长路径上的节点总数。
N 叉树输入按层序遍历序列化表示,每组子节点由空值分隔(请参见示例)。
示例 1:
输入:root = [1,null,3,2,4,null,5,6] 输出:3示例 2:
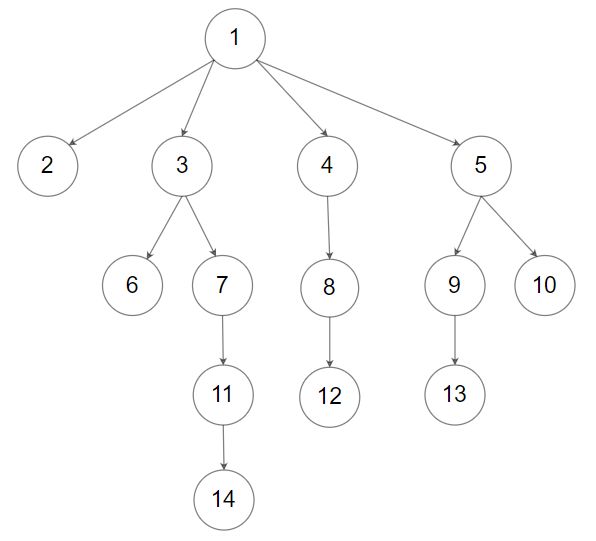
输入:root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14] 输出:5提示:
- 树的深度不会超过
1000。- 树的节点数目位于
[0, 104]之间。
这道题目和上一道题目的思路一样,只不过从遍历一个节点的左右孩子变成了遍历一个节点的孩子,下面我们直接给出后序遍历的代码。
(1)Python版本代码
"""
# Definition for a Node.
class Node:
def __init__(self, val=None, children=None):
self.val = val
self.children = children
"""
class Solution:
def maxDepth(self, root: 'Node') -> int:
if not root:
return 0
depth = 0
for i in range(len(root.children)):
depth = max(depth, self.maxDepth(root.children[i]))
return depth + 1
(2)C++版本代码
/*
// Definition for a Node.
class Node {
public:
int val;
vector children;
Node() {}
Node(int _val) {
val = _val;
}
Node(int _val, vector _children) {
val = _val;
children = _children;
}
};
*/
class Solution {
public:
int maxDepth(Node* root) {
if (root == NULL) return 0;
int depth = 0;
for (int i = 0; i < root->children.size(); i++) {
depth = max (depth, maxDepth(root->children[i]));
}
return depth + 1;
}
};
3 LeetCode 111.二叉树的最小深度
题目链接:https://leetcode.cn/problems/minimum-depth-of-binary-tree/description/
给定一个二叉树,找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
**说明:**叶子节点是指没有子节点的节点。
示例 1:
输入:root = [3,9,20,null,null,15,7] 输出:2示例 2:
输入:root = [2,null,3,null,4,null,5,null,6] 输出:5提示:
- 树中节点数的范围在
[0, 105]内-1000 <= Node.val <= 1000
上面两题是求二叉树的最大深度,本题刚好相反,有相同的地方,也有不同的地方,首先递归终止条件肯定一样,然后也是需要判断根节点左右子树是否为空,如果仅左子树为空,那么二叉树就只剩下右子树,也就类似于链表的结构,此时最小深度也就是树高,同理仅右子树为空也是这样,唯一不同的是如果左右子树都不为空,那么我们就需要返回深度更小的高度,这样我们就可以得到二叉树的最小深度了。
下面我们来写出对应的代码,从上面分析我们不难看出使用的是递归法中的后序遍历。
(1)Python版本代码
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def minDepth(self, root: Optional[TreeNode]) -> int:
if not root:
return 0
if not root.left: # 左子树为空
return self.minDepth(root.right) + 1 # 返回右子树的最小深度 + 1
if not root.right: # 右子树为空
return self.minDepth(root.left) + 1 # 返回左子树的最小深度 + 1
return min(self.minDepth(root.left), self.minDepth(root.right)) + 1 # 左右子树都不为空,返回左右子树最小深度的较小值 + 1
(2)C++版本代码
#include 4 LeetCode 222.完全二叉树的节点个数
题目链接:https://leetcode.cn/problems/count-complete-tree-nodes/description/
给你一棵 完全二叉树 的根节点
root,求出该树的节点个数。完全二叉树 的定义如下:在完全二叉树中,除了最底层节点可能没填满外,其余每层节点数都达到最大值,并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第
h层,则该层包含1~ 2h个节点。示例 1:
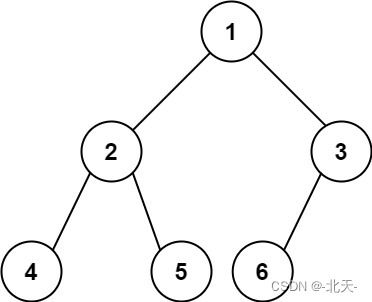
输入:root = [1,2,3,4,5,6] 输出:6示例 2:
输入:root = [] 输出:0示例 3:
输入:root = [1] 输出:1提示:
- 树中节点的数目范围是
[0, 5 * 104]0 <= Node.val <= 5 * 104- 题目数据保证输入的树是 完全二叉树
**进阶:**遍历树来统计节点是一种时间复杂度为
O(n)的简单解决方案。你可以设计一个更快的算法吗?
这道题目最好实现的思路就是把完全二叉树当作一棵普通的二叉树来计算,这样思路会非常的清晰,代码也非常的简短,时间复杂度也就是遍历二叉树所花费的时间:O(n),我们最好采用后序遍历的方法来实现,相比于前序和中序代码更好写,我们只需要分别统计左子树和右子树的节点数量,最后加上根节点即可。
4.1 普通遍历
(1)Python版本代码
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def countNodes(self, root: Optional[TreeNode]) -> int:
if not root:
return 0
leftNums = self.countNodes(root.left)
rightNums = self.countNodes(root.right)
result = leftNums + rightNums + 1
return result
(2)C++版本代码
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int countNodes(TreeNode* root) {
if (root == NULL) return 0;
int leftNums = countNodes(root->left);
int rightNums = countNodes(root->right);
int reslut = leftNums + rightNums + 1;
return reslut;
}
};
4.2 利用完全二叉树的特性优化遍历
题目给出的是一棵完全二叉树,所以我们还可以用完全二叉树的特性进行剪枝操作,比如,如果一棵子树,它的左右子树如果高度一样,那么它就是一棵满二叉树,因为如果中间叶子节点缺失那么它就不满足题目条件就不是一棵完全二叉树了(完全二叉树的介绍可以看前几期的博客,另外二叉树的各种类型及其特性是需要牢记于心的),如果满足左右子树高度相等的话,这个时候我们就可以直接使用对应计算满二叉树节点数的公式( 2 h − 1 , h 为二叉树的高度 2^h-1,h为二叉树的高度 2h−1,h为二叉树的高度)计算其节点总数,最后再相加起来即可。
下面是实现的代码。
(1)Python版本代码
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def countNodes(self, root: Optional[TreeNode]) -> int:
if not root:
return 0
left = root.left
right = root.right
leftHight = 0
rightHight = 0
while left:
left = left.left
leftHight += 1
while right:
right = right.right
rightHight += 1
if leftHight == rightHight:
return (2 << leftHight) - 1
leftNums = self.countNodes(root.left)
rightNums = self.countNodes(root.right)
result = leftNums + rightNums + 1
return result
(2)C++版本代码
class Solution {
public:
int countNodes(TreeNode* root) {
if (root == nullptr) return 0;
TreeNode* left = root->left;
TreeNode* right = root->right;
int leftDepth = 0, rightDepth = 0; // 这里初始为0是有目的的,为了下面求指数方便
while (left) { // 求左子树深度
left = left->left;
leftDepth++;
}
while (right) { // 求右子树深度
right = right->right;
rightDepth++;
}
if (leftDepth == rightDepth) {
return (2 << leftDepth) - 1; // 注意(2<<1) 相当于2^2,所以leftDepth初始为0
}
return countNodes(root->left) + countNodes(root->right) + 1;
}
};