【牛客网题目解析：从入门到精通的秘籍】173道基础题详解 (第三期）

本文作者：大家好，我是原始豌豆，欢迎来到牛客网刷题解析第三期，感谢你阅读本文欢迎评论，收藏，点赞哦。
内容专栏：这里是《牛客网在线编程》专栏，笔者用重金(时间和精力)打造，每道题目提供多种解法，从基础到拓展，希望可以帮到读者们。
：写作不易，本文对每道题目提供了多种解法并加上了详细的注释，意在帮助读者锻炼思维灵活性，提高分析、解决问题的能力)。

开端
     本次爆更，全篇共13826字，详细解析了每道题目，对其中一些题目采用了四到五种解法，并详细讲解了其中蕴含的算法思想和数学公式，在这篇文章中，我将分享刷题过程中的一些感悟、技巧和策略。同时，我也会分享一些个人的学习心得和经验，希望能帮助到同样热爱编程的你。

     一段寻找自我与极限的旅程，让我们一起踏上这段奇妙的C语言刷题之旅吧！！！！

题目目录

牛客网语法篇基础语法31-50题（C语言实现)

题目网址链接请点这✌️

标注“ * ”符号的题目为重点题目(“ * ” 数越多，难度越高)
本页目录跳转请点下方

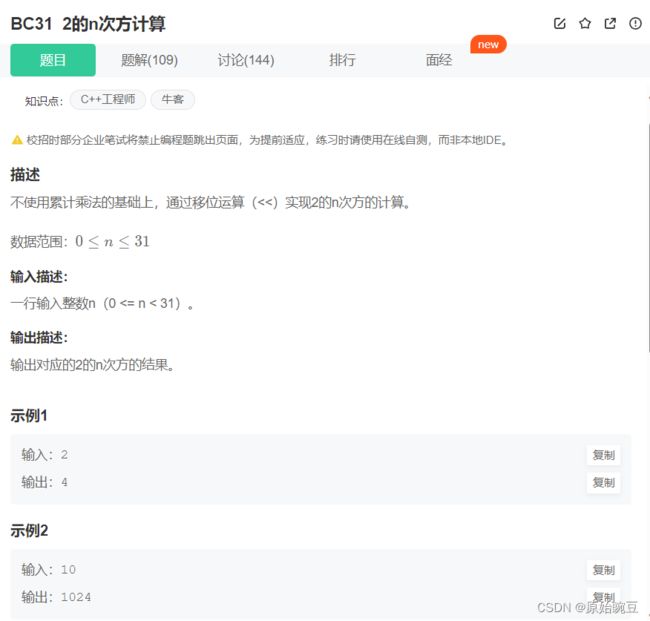
BC31 2的n次方计算 *
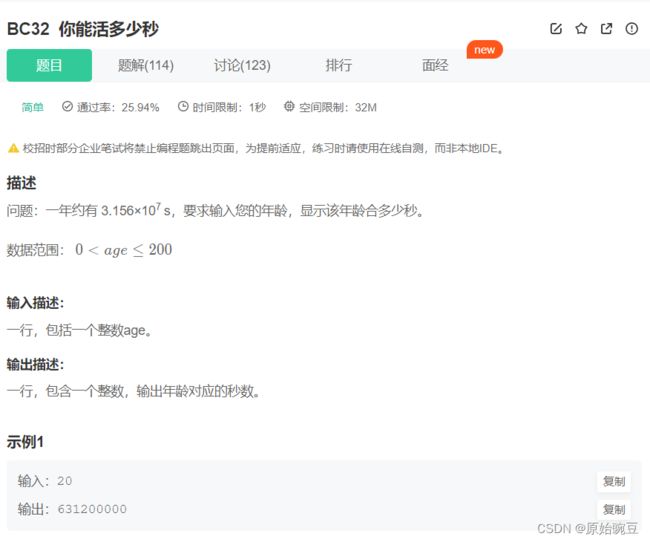
BC32 你能活多少秒
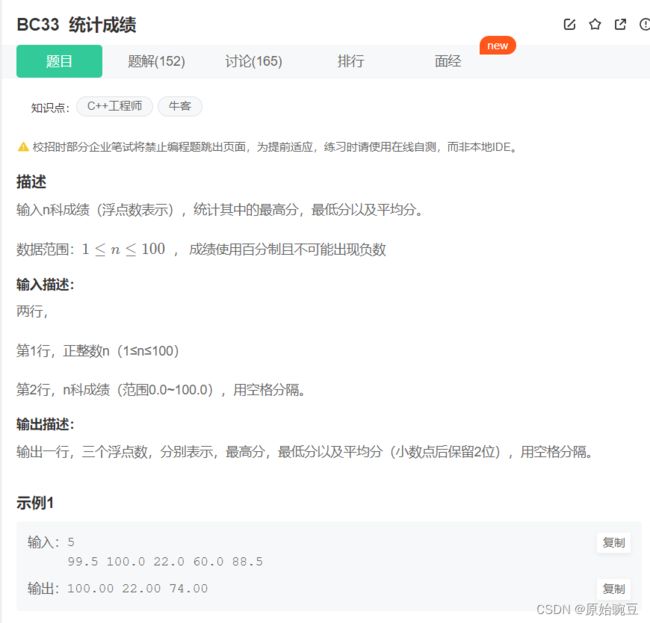
BC33 统计成绩 *
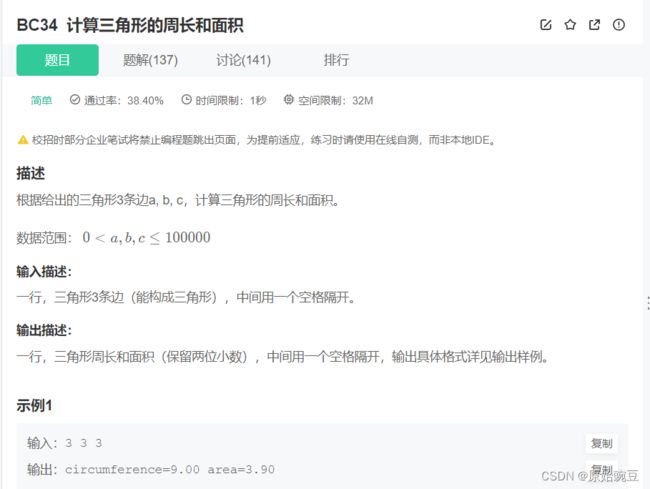
BC34 计算三角形的周长和面积
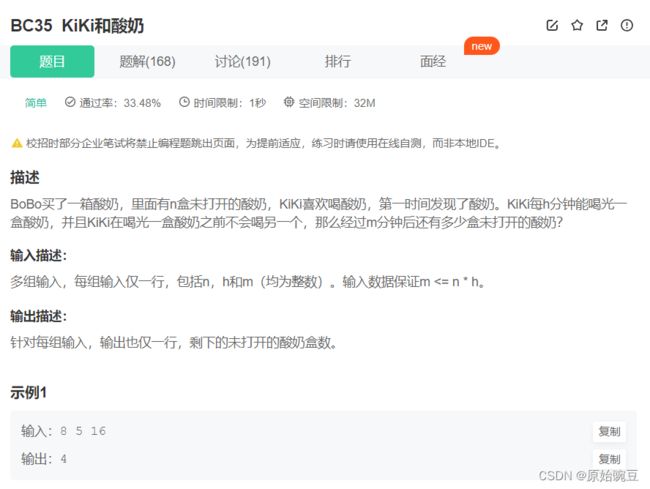
BC35 KiKi和酸奶 *
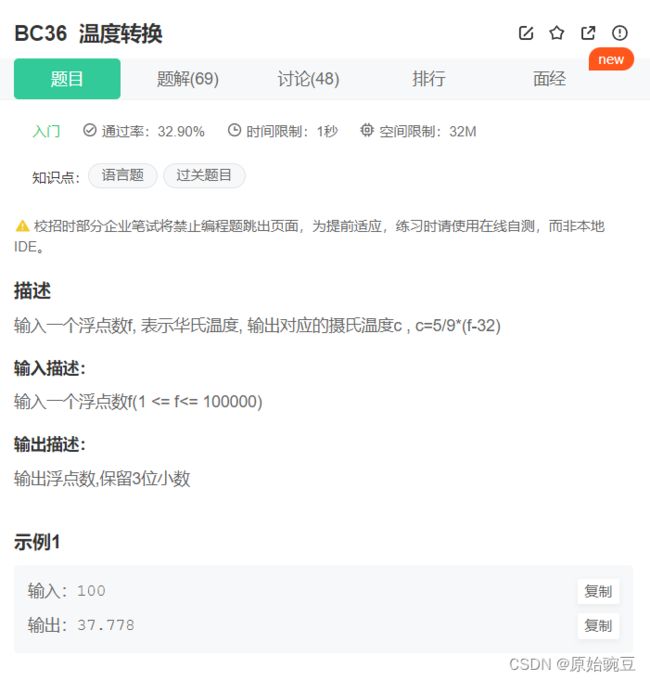
BC36 温度转换
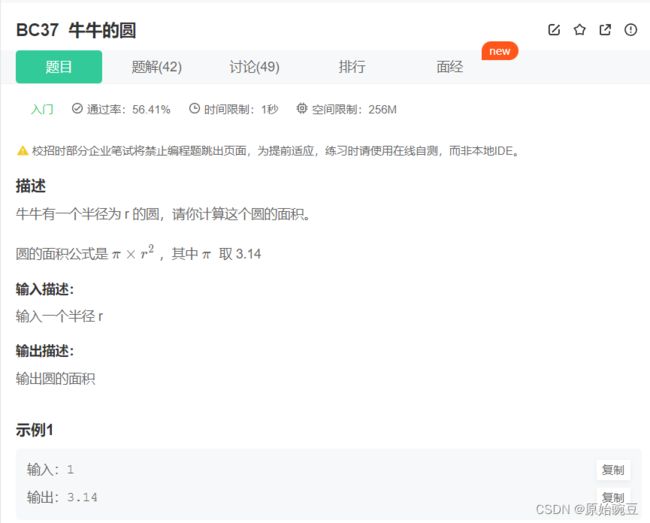
BC37 牛牛的圆
BC38 牛牛的并联电路
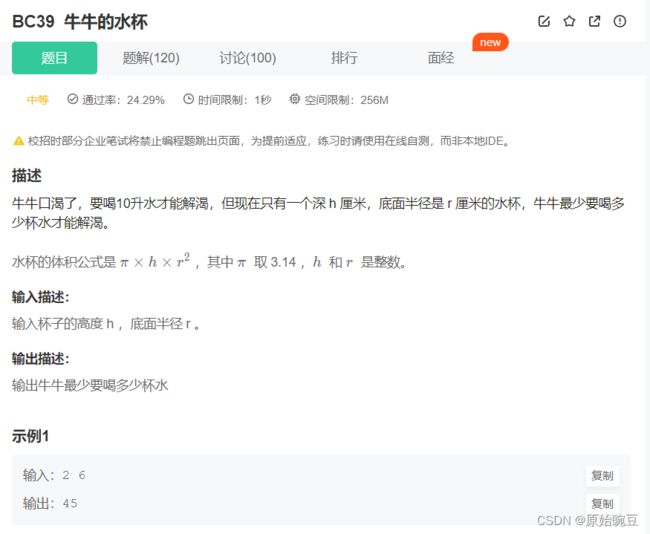
BC39 牛牛的水杯 *
BC40 牛牛的等差数列
BC41 牛牛的球
BC42 小乐乐定闹钟 *
BC43 小乐乐排电梯
BC44 (小乐乐与欧几里得)最大公约数与最小公倍数问题 **
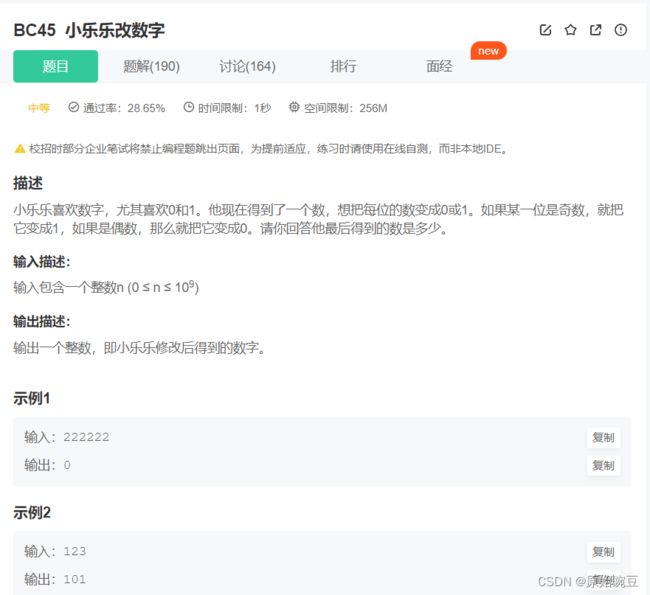
BC45 小乐乐改数字 **
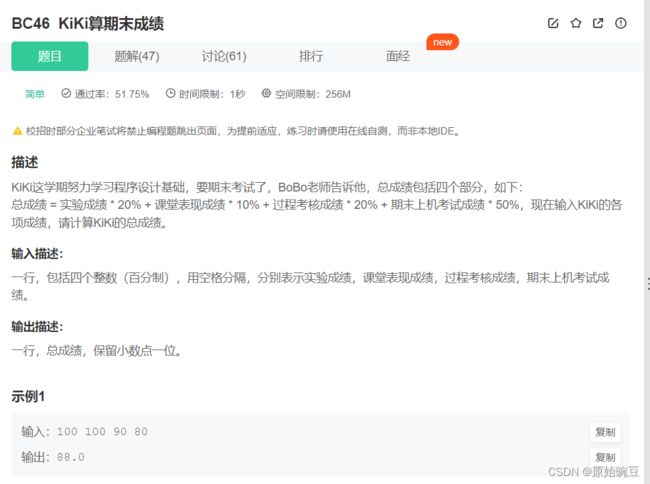
BC46 KiKi算期末成绩
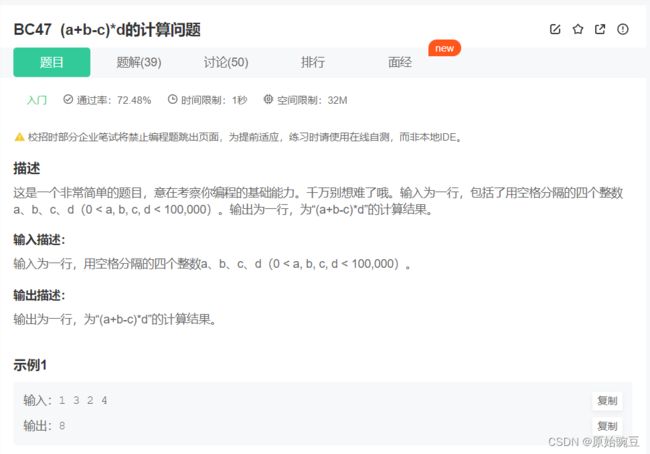
BC47 (a+b-c)*d的计算问题
BC48 牛牛的线段
BC49 kiki算数
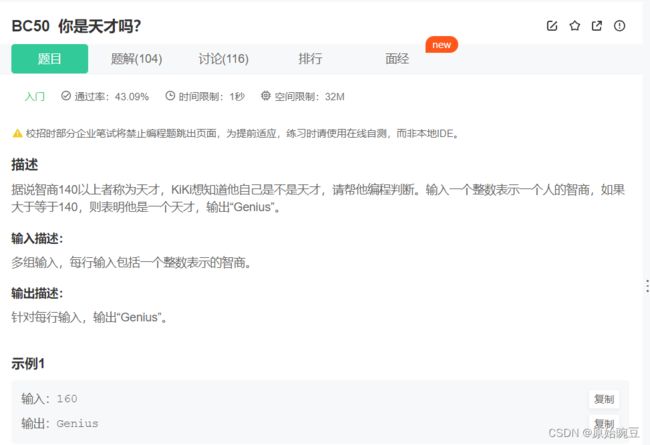
BC50 你是天才么？

题目

BC31 2的n次方计算

//在2进制中，2的表示为00000010
//我们只使用移位符来完成2的n次方，仅需使这个2的二进制中的1往左移动。
//如4：二进制为00000100；8：二进制为00001000
//解法一
#include 
int main() {
    int n;
    scanf("%d", &n);
    if (n == 0)//n=0时要单独判断一下，因为2^0=1
        printf("%d", 1);
    else
        printf("%d", 2 << (n- 1));//要注意为什么这里是（n-1），因为2本身已经在第二位了，是2的1次方。
    return 0;
}

//解法二  直接将1左移n位数，1的二进制位就是1，n=0时(即2的0次方)，1左移0位还是1，n=3时，1左移三位变为100，即2的3次方8。
//这样可以解决计算2的0次方时，在解法一里需要单独判断的问题
#include 
int main() {
    int n = 0;
    scanf("%d", &n);
    int ret = 1 << n;  // 使用位操作符左移n位，实际上就是计算2的n次方。  
    printf("%d", ret);
    return 0;
}

BC32 你能活多少秒

#include 
#include // 引入数学库，使得我们可以使用pow函数进行幂运算。  
int main() {
    int age = 0;// 定义一个整数变量age，并初始化为0。这将是用户输入的年龄。
    long sec = 0;// 定义一个长整数变量sec，用于存储以秒为单位的时间。初始化为0。  
    scanf("%d", &age);
    sec = age * 3.156 * pow(10, 7);//使用pow函数计算3.156*10^7的值
    printf("%ld", sec);
    return 0;
}

BC33 统计成绩

//解法一 利用变长数组解决
#include 
int main() {
    int n = 0;
    float sum = 0.0f;
    float lower = 100.0f,higher = 0.0f;// 定义两个浮点变量lower和higher，用于存储数据中的最小值和最大值，初始值分别为100和0
    scanf("%d", &n);// 从标准输入读取一个整数n，表示数组的长度 
    float f[n];//变长数组不能初始化，C99标准以后支持变长数组
    for (int i = 0; i < n; i++) {
        scanf("%f", &f[i]);//输入五个数据，存入数组，存放时每个数据都跟最大最小值比较一下
        if (f[i] < lower)// 如果读取的数据小于当前最小值，则更新最小值  
            lower = f[i];
        else if (f[i] > higher)//如果读取的数据大于当前最大值，则更新最大值 
            higher = f[i];
        sum += f[i];
    }
    printf("%.2f %.2f %.2f", higher, lower, sum / n);// 输出最大值、最小值和平均值，保留两位小数  
    return 0;
}
//解法二 通过循环每次比较输入的数值和最大最小值的大小，然后更新最大或最小值
//因为有输入缓冲区，所以数据不用存放在数组里
#include 
int main() {
    int n = 0;
    float sum = 0.0f;
    float score = 0.0f;
    float lower = 100.0f,higher = 0.0f;// 定义两个浮点变量lower和higher，用于存储数据中的最小值和最大值，初始值分别为100和0
    scanf("%d", &n);// 从标准输入读取一个整数n，表示数据的数量  
    for (int i = 0; i < n; i++) {
        scanf("%f", &score);//输入五个数据，是存在输入缓冲区中的，所以可以不用数组
        if (score < lower)// 如果读取的数据小于当前最小值，则更新最小值  
            lower = score;
        else if (score > higher)//如果读取的数据大于当前最大值，则更新最大值  if-else if结构比双if结构效率更高
            higher = score;
        sum += score;
    }
    printf("%.2f %.2f %.2f", higher, lower, sum / n);// 输出最大值、最小值和平均值，保留两位小数  
    return 0;
}

BC34 计算三角形的周长和面积

//海伦公式，又译作希伦公式、海伦-秦九韶公式。它是利用三角形的三条边的边长直接求三角形面积的公式。表达式为：S=√p(p-a)(p-b)(p-c)。其中p = (a + b + c) / 2;
#include
int main() {
    double a, b, c, p, l, s;//定义三边长a,b,c定义半周长p,定义周长l,定义面积s
    scanf("%lf%lf%lf", &a, &b, &c);
    p = (a + b + c) / 2;
    l = a + b + c;
    s = sqrt(p * (p - a) * (p - b) * (p - c));//海伦公式//sqrt参数和返回值都是double类型
    printf("circumference=%.2lf area=%.2lf", l, s);
    return 0;
}

BC35 KiKi和酸奶

//解法一
#include 
int main() {
    int n, h, m;//n表示酸奶总数，h表示喝一盒酸奶需要的分钟数。
    while (scanf("%d%d%d", &n, &h, &m) != EOF) {
        if (m <= n * h )
            printf("%d", ( m % h ) ? n - (m / h + 1) : (n - m / h));
        //如果m除以h有余数（即m % h)不为0，就要多开一盒，三目运算符就会计算n - (m / h + 1)并打印结果。n - (m / h + 1)表示经过m分钟后未打开的酸奶，
        //如果m除以h的余数为0（即m能被h整除）就不会再有额外打开的酸奶，三目运算符就会计算(n - m / h)的结果，商是几就喝了几盒酸奶
    }
}
//解法二 利用ceil函数计算向上取整的值，ceil函数计算的是大于或等于这个数的最小整数值，参数和返回值都是double类型。
#include
#include
int main() {
    double n, h, m,num;
    scanf("%lf%lf%lf", &n, &h, &m);
    num=ceil(m / h);//m/h无法整除的情况下，得到的会是一个浮点数，喝的酸奶数实际是这个浮点数向上取整的结果，
    printf("%d", (int)(n - num));//n-num就是剩余酸奶数
    return 0;
}
//解法三 利用浮点数能计算准确除法和强制类型转换后截断取整的性质计算剩余酸奶数
#include
int main() {
    float n, h, m;
    scanf("%f%f%f", &n, &h, &m);
    printf("%d", (int)(n - (m / h)));//m/h无法整除的情况下，得到的会是一个浮点数，喝的酸奶数实际是这个浮点数向上取整的结果，
    //用n减去这个浮点数，之后在强制类型转换截断取整，相当于总酸奶数把m/h的浮点数向上取整的结果减掉了。
    return 0;
}

BC36 温度转换

#include
int main() {
float f = 0.0f;
float c = 0.0f;
scanf("%f", &f);
c = 5.0 / 9 * (f - 32);//除法这里要改成浮点数5.0，否则会执行整数除法，结果会==0
printf("%.3f", c);
return 0;
}

BC37 牛牛的圆

#include
int main() {
    float r;
    scanf("%f", &r);
    printf("%f", r * r * 3.14);
    return 0;
}

BC38 牛牛的并联电路

#include
int main() {
    float r1, r2, r3;//注意r1,r2,r3都设置为浮点数，方便进行除法
    scanf("%f %f", &r1, &r2);
    r3 = 1 / ((1 / r1) + (1 / r2));
    printf("%.1f", r3);
    return 0;
}

BC39 牛牛的水杯

//解法一  不可以用求余号，因为%两边操作数要求均是整数
#include
int main()
{
    int h = 0, r = 0;
    scanf("%d%d", &h, &r);
    float v = h * 3.14 * r * r;
    int c = 10000;//水的体积
    int d = 0;
    while (c > 0)
    {
        c = c - v;
        d++;
    }
    printf("%d", d);
    return 0;
}

//解法二
#include
int main() {
    float n1, v;//定义n1用来存放1L水除以杯子的体积有多少杯(浮点数) v是杯子的体积
    int h, r, n2;//h,r表示杯子的高和底面半径，整型n2存放截断取整后的n1值
    scanf("%d%d", &h, &r);
    v = 3.14 * h * r * r;
    n1 = 10000 / v;
    n2 = (int)n1;
    //如果n1的结果是小数，则喝的杯数是小数向上取整（这里通过n1截断取整的值+1得到小数向上取整的值）
    //如果整除了，则喝的杯数就是商
    printf("%d", n1 - n2 > 0 ? n2 + 1 : n2);//三目运算符判断杯数是否整除，未整除则n2+1,整除则n2
    
}

//解法三
#include
#include 
int main() {
    int h, r;//h,r表示杯子的高和底面半径
    float v;//v是杯子的体积
    scanf("%d %d", &h, &r);
    v = 3.14 * h * pow(r, 2);//计算杯子容积
    printf("%d", (int)ceil(10000 / v));//杯数向上取整，ceil返回值是浮点型，所以强制类型转换一下
    return 0;
}

BC40 牛牛的等差数列

//解法一   等差数列公式an=a1+(n-1)d
#include 
int main() {
    int a, b, c;
    int d;//公差d
    scanf("%d%d", &a, &b);
    d = b - a;//算出等差数列公差d
    c = a + 2 * d;//首项+（第几项的项数-1)*公差d
    printf("%d", c);
}

//解法二  直接算
int main() {
    int a;
    int b;
    scanf("%d %d", &a, &b);
    printf("%d", b + b - a);
    return 0;
}

BC41 牛牛的球

#include 
int main() {
   float r;
   float v;
   scanf("%f",&r);
   v=(4.0/3)*3.14*r*r*r;//注意4.0/3才能执行浮点数除法
   printf("%.2f",v);
   return 0;
}

BC42 小乐乐定闹钟

//解法一
#include 
int main() {
    int hour, min, k,total; //定义四个变量hour,min代表输入的现在的时刻的小时数，分钟数。k代表要睡的分钟数，total代表总分钟数
    int h = 0;
    int m = 0;
    scanf("%d:%d %d", &hour, &min, &k);
    total = hour * 60 + min +k;//将当前的时间全转换为分钟数并加上要睡的分钟数
    h = total / 60 % 24;//总分钟数转换为小时数并%24代表几时
    m = total % 60;//总分钟数%60代表显示的分钟数
    printf("%02d:%02d", h, m);
    return 0;
}

//解法二
int main()
{
    int hour, minute, k;
    scanf("%d:%d %d", &hour, &minute, &k);//输入
    hour += k / 60;//增加小时
    minute += k % 60;//增加分钟
    if (minute > 59)//如果分钟大于59，将分钟调整为0~59，并将小时加1。
    {
        minute -= 60;
        hour++;
    }
    while (hour > 23)//如果小时大于23，将小时调整为0~23。
    {
        hour -= 24;
    }
    printf("%02d:%02d", hour, minute);//输出
    return 0;
}

//解法三
int main()
{
    int h = 0;
    int m = 0;
    int k = 0;
    scanf("%d:%d %d", &h, &m, &k);
    h = (h + (k + m) / 60) % 24;//计算小时，因为不考虑日期，所以先计算得到总共多少小时，再对24取余，以防出现大于24的情况
    m = (k + m) % 60;//看剩下多少分钟
    printf("%02d:%02d\n", h, m);
    return 0;
}

BC43 小乐乐排电梯

#include
int main () {
    int n = 0;
    int time = 0;
    scanf("%d", &n);//不用判断人数是否小于12
    time = n / 12 * 4 + 2;//小于12时，time=2,所以不用额外判断
    printf("%d", time);
}

BC44 (小乐乐与欧几里得)最大公约数与最小公倍数问题

//方法一  此方法的时间复杂度过大，在牛客网测试时超过运行时间，所以不推荐
int main() { //试除法
	long  num1, num2, comax, comin; //定义两个数字num1,num2,最大公约数comax,最小公倍数comin
	scanf("%ld %ld", &num1, &num2);
	comax = num1 < num2 ? num1 : num2;// 找到 num1 和 num2 中的较小值作为最大公约数
	comin = num1 > num2 ? num1 : num2;// 找到 num1 和 num2 中的较大值作为最小公倍数
	while (comax) {
		if (num1 % comax == 0 && num2 % comax == 0)//检查 num1，num2 是否能同时被comax整除。如果能，那么说明 min 是 num1 和 num2 的公约数。
			break;                             //又因为是从comax(num1和num2的较小值开始试除)，所以得到的一定是两个数的最大公约数
		comax--;// 如果上述条件不为真，则将 comax 的值减1，然后再次循环试除
	}
	while (comin) {
		if (comin % num1 == 0 && comin % num2 == 0)//检查comin是否能同时被num1，num2 整除。如果能，那么说明comin是num1和num2的公约数。
			break;                                   //又因为num1和num2的较大值comin(开始试除num1和num2)，所以得到的一定是两个数的最大公约数
		comin++;// 如果上述条件不为真，则将comin的值加1，然后再次检查。
	}
	printf("%ld\n", comax + comin);
}

//方法二
//辗转相除法是一种计算两个整数的最大公约数（GCD）的算法。以下是使用辗转相除法的计算例子：
//假设我们有两个整数 120 和 48，我们要计算它们的最大公约数。
//步骤如下：
//用较大的数除以较小的数，得到余数：120 % 48 = 24。
//将上一步中的除数作为新的被除数，原来的余数作为新的除数继续计算：48 % 24 = 0。
//由于余数为0，所以此时除数24就是120和48的最大公约数。
//因此，120和48的最大公约数是24。
//而得到了最大公约数的情况下，输入的两数相乘的结果减去最大公约数就是最小公倍数。
#include 
int main()
{
	long num1, num2, num3; //声明三个整型变量num1、num2和num3,分别代表被除数，除数，余数
	scanf("%ld %ld",&num1,&num2);
    long tmp=num1*num2;//tmp用于存放num1*num2的值，用于后续计算最小公倍数时用
 //这里不需要判断被除数，除数大小。假设被除数16，除数24，16%24==16 ，再将除数赋值给被除数。
 // 余数赋值给除数后变为24%16，所以会一直保证被除数比除数大所以无需判断被除数和除数大小
	while ((num3=num1%num2))//计算余数并赋给num3,同时num3也是循环终止条件，num3==0时则循环终止
	{
		num1 = num2; //将num2的值赋给num1。
		num2 = num3;//将num3的值赋给num2。
	}
	//余数为0时，循环结束，除数的值(num2)就是最大公约数
	printf("%ld\n",num2+tmp/num2);//tmp的值除以num2(最大公约数)的值就是最小公倍数
	return 0;
}

//方法三，更相减损术
// 比较两数大小，用大数减小数，得到一个差。
// 对差和减数作比较，继续以大数减去小数
// 重复上述过程，直到差和减数相等时，(即下一次的被减数和减数相等时)。
// 这时，相等的数就是a和b的最大公约数。
//例：用更相减损术求98与63的最大公约数。
//解：把98和63以大数减小数，并辗转相减：
//98 - 63 = 35
//63 - 35 = 28
//35 - 28 = 7
//28 - 7 = 21
//21 - 7 = 14
//14 - 7 = 7
//所以，98和63的最大公约数等于7
#include 
int main()
{
	long num1, num2,num3,tmp,product;//声明三个整型变量num1、num2,num3分别代表被减数，减数,差和临时变量tmp
	scanf("%ld %ld", &num1, &num2);
	product=num1*num2;
	product=num1*num2;
	while (num1 != num2)
	{
		if (num1 > num2)
		{
			num3 = num1 - num2;//计算差值
			num1 = num2;//先把num2赋值给num1.（减数变成被减数）
			num2 = num3;//num3的值赋给num2   （差变成被减数）
		}
		else if (num2 > num1)//减数>被减数时，用临时变量tmp,交换减数和被减数的值，确保被减数永远大于减数
		{
			tmp = num1;
			num1 = num2;
			num2 = tmp;
		}
	}
printf("%ld\n",num2+product/num2);//tmp的值除以num2(最大公约数)的值就是最小公倍数
}

//方法四 对更像减损术的优化和不依靠最大公约数单独求两个数最小公倍数的方法
//该算法优化了更像减损术，但是单独计算最小公倍数时，时间复杂度会较大。牛客网大数测试时超时
#include 
int main() {
	long num1, num2; //声明整型变量num1、num2分别代表要操作的两个数（被减数，减数）.
	scanf("%ld %ld", &num1, &num2);
	long a = num1;
	long b = num2;
	while (num1 != num2) {
		if (num1 > num2)
			num1 -= num2;
		else
			num2 -= num1;
	}
	int i = 1;//创建个 while 循环, if 判断 a * i % b==0
//看 a 乘于 i 得出的数看能不能被 b 整除,如果可以那么它就是最小公倍数
	while ((a * i) % b != 0)
		i++;
	printf("%ld", num1 + i * a);
}

BC45 小乐乐改数字

//解法一  利用自定义函数求出输入数字的长度，从左向右不断取出输入数字的每一位，判断奇偶（奇1偶0），然后乘以该数字原先所对应的权数
#include
#include 
int fun(int n) {//计算一个整数有几位数的自定义函数
    int count = 0;
    while (n > 0) {
        count++;
        n = n / 10;
    }
    return count;
}
int main() {
    int n, first_number, sum = 0;
    scanf("%d", &n);
    int count = fun(n);//计算输入的数字有几位数
    while (count > 0) {
        first_number = n / pow(10, count - 1);//取出这个数字的第一位，count-1代表这个数字对应的权数是几。
        n %= (int)pow(10, count - 1);//将数字首位去掉
        first_number = first_number % 2 == 0 ? 0 : 1;//判断取出的数字是奇数还是偶数
        first_number = first_number * (int)pow(10, count - 1);//(1或0)乘以这个十进制数字的每位数字原来对应的的权数
        sum += first_number;//不断累加
        count--;//数字位数--
    }
    printf("%d", sum);
    return 0;
}

//解法二  将输入数字的转换成字符串存放在数组里，数组最后一位为'\0',利用字符串函数算出整数长度,遍历数组进行奇1偶0转换，乘以对应的权数后不断累加，最后再以字符串的形式打印出来。
#include
#include 
#include 
int main() {
    char ch[11] = { '\0' };
    scanf("%s", ch);
    int len = strlen(ch);//字符串长度，即输入数字的数字长度
    int sum = 0;
    int tmp = 0;
    for (int i = 0; i < len; i++) {
        tmp = (ch[i] % 2 == 0 ? 0 : 1);//判断字符串每个数字字符的奇偶，是偶数就赋值0給tmp,是奇数赋值1给tmp 
         //这里注意一下，ch[i]里存放的是数字字符，取模运算时转换成Ascll码%2，判断是否奇偶，而数字字符0-9对应的Ascll码值48-57，也刚好是奇偶对应。所以不用刻意将数字字符转换成数字(转换方法ch[i]-'0')
        tmp *= (int)pow(10.0, (double)len - i - 1);//(1或0)乘以这个十进制数字的每位数字原来对应的的权数
        sum = sum + tmp;
    }
    printf("%d", sum);
    return 0;
}

//解法三  从右向左不断取出输入数字的每一位，然后（奇1偶0），然后乘以该数字原先所对应的权数
int main() {
    int n = 0, i = 0, ret = 0;
    scanf("%d", &n);
    while (n) {
        int w = n % 10 % 2;//模10取出最后一位，在模2，如果是偶数模2刚好等于0，奇数模2刚好等于1，所以不用额外判段奇偶
        ret += w * pow(10, i++);//每运算一次权数i自增一次
        n /= 10;
    }
    printf("%d\n", ret);
    return 0;
}

//解法四是解法三的递归写法，思想相同，只不过是采用了递归
int digui(int n) {
    int c = n % 10 % 2;
    if (n /= 10)
        return 10 * digui(n) + c;
    return c;
}
int main() {
    int n = 0;
    scanf("%d", &n);
    int a = digui(n);
    printf("%d", a);
    return 0;
}

BC46 KiKi算期末成绩

#include //基础题。
int main() {
    int s, k, g, q;
    float sum;
    scanf("%d %d %d %d", &s, &k, &g, &q);
    sum = s * 0.2 + k * 0.1 + g * 0.2 + q * 0.5;
    printf("%.1f", sum);
    return 0;
}

BC47 (a+b-c)*d的计算问题

#include //基础题
int main() {
    int a, b, c, d;
    scanf("%d%d%d%d", &a, &b, &c, &d);
    int sum = (a + b - c) * d;
    printf("%d", sum);
    return 0;
}

BC48 牛牛的线段

#include //基础题
int main() {
    int a, b, c, d;
    scanf("%d%d%d%d", &a, &b, &c, &d);
    int sum = (a - c) * (a - c) + (b - d) * (b - d);
    printf("%d", sum);
    return 0;
}

BC49 kiki算数

/*只保留该数的最后两位，例如：对KiKi来说1234等价于34；
如果计算结果大于等于 100， 那么KIKI也仅保留计算结果的最后两位，如果此两位中十位为0，则只保留个位。
对本题而言，由于计算过程只是每个数字的后两位参与，根据加法的性质，直接对(a+b)%100结果也是等价的*/
#include 
int main() {
    int a, b;
    scanf("%d%d", &a, &b);
    int sum = (a + b) % 100;
    printf("%d", sum);
    return 0;
}

BC50 你是天才么？

#include 
int main() {
    int a, b;
    while (scanf("%d", &a) != EOF) { //注意题目是多行输入，所以我们用while (scanf("%d", &a) != EOF) 
        if (a>=140)
        printf("Genius\n");
    }
    return 0;
}

总结：
    整个解析过程，本次的题目很考验数学功底，数学注重逻辑推理和问题解决，这种思维方式在编程中同样非常重要。数学好的人通常更容易理解复杂的算法和数据结构，能够更快地找到解决问题的方法。
    数学培养了抽象思维的能力，能够将具体的问题抽象化，从而更好地进行编程。在计算机科学中，抽象是非常重要的，它可以帮助我们更好地理解和操作复杂的系统和概念。

    本文对每道题目都提供了多种解法和一些独特的解法，参考了数学公式，比如通过求两个数的最大公约数问题里，采用了辗转相除法，更相减损数等数学定理。比如计算三角形三边面积时采用的海伦公式，数学在编程中的优势是多方面的，它不仅能够帮助我们更好地理解算法和数据结构，还能够帮助我们更好地进行问题解决和程序设计。因此，对于想要成为优秀的程序员的人来说，具备良好的数学基础是非常重要的。技巧，为未来的学习和工作打下坚实的基础。