LeetCode852. 山脉数组的峰顶索引 / 374. 猜数字大小 / 278. 第一个错误的版本 / 第 54 场双周赛 / 第 245 场周赛
852. 山脉数组的峰顶索引
2021.6.15每日一题
题目描述
符合下列属性的数组 arr 称为 山脉数组 :
arr.length >= 3
存在 i(0 < i < arr.length - 1)使得:
arr[0] < arr[1] < ... arr[i-1] < arr[i]
arr[i] > arr[i+1] > ... > arr[arr.length - 1]
给你由整数组成的山脉数组 arr ,返回任何满足 arr[0] < arr[1] < ... arr[i - 1] < arr[i] > arr[i + 1] > ... > arr[arr.length - 1] 的下标 i 。
示例 1:
输入:arr = [0,1,0]
输出:1
示例 2:
输入:arr = [0,2,1,0]
输出:1
示例 3:
输入:arr = [0,10,5,2]
输出:1
示例 4:
输入:arr = [3,4,5,1]
输出:2
示例 5:
输入:arr = [24,69,100,99,79,78,67,36,26,19]
输出:2
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/peak-index-in-a-mountain-array
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路
已经连续第三天是一道简单的二分查找了,咋回事,说好的动规呢???
二分第一种写法,(向上取整)
class Solution {
public int peakIndexInMountainArray(int[] arr) {
//怎么突然连续三天变成二分查找了
int l = arr.length;
int left = 1;
int right = l - 1;
while(left < right){
int mid = (right - left + 1) / 2 + left;
if(arr[mid] < arr[mid - 1]){
right = mid - 1;
}else{
left = mid;
}
}
return left;
}
}
374. 猜数字大小
2021.6.14每日一题
题目描述
猜数字游戏的规则如下:
每轮游戏,我都会从 1 到 n 随机选择一个数字。 请你猜选出的是哪个数字。
如果你猜错了,我会告诉你,你猜测的数字比我选出的数字是大了还是小了。
你可以通过调用一个预先定义好的接口 int guess(int num) 来获取猜测结果,返回值一共有 3 种可能的情况(-1,1 或 0):
-1:我选出的数字比你猜的数字小 pick < num
1:我选出的数字比你猜的数字大 pick > num
0:我选出的数字和你猜的数字一样。恭喜!你猜对了!pick == num
返回我选出的数字。
示例 1:
输入:n = 10, pick = 6
输出:6
示例 2:
输入:n = 1, pick = 1
输出:1
示例 3:
输入:n = 2, pick = 1
输出:1
示例 4:
输入:n = 2, pick = 2
输出:2
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/guess-number-higher-or-lower
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路
二分第二种写法
public class Solution extends GuessGame {
public int guessNumber(int n) {
int left = 1;
int right = n;
while(left <= right){
int mid = (right - left) / 2 + left;
if(guess(mid) == 0){
return mid;
}else if(guess(mid) == 1)
left = mid + 1;
else
right = mid - 1;
}
return left;
}
}
278. 第一个错误的版本
2021.6.13每日一题
题目描述
你是产品经理,目前正在带领一个团队开发新的产品。不幸的是,你的产品的最新版本没有通过质量检测。由于每个版本都是基于之前的版本开发的,所以错误的版本之后的所有版本都是错的。
假设你有 n 个版本 [1, 2, ..., n],你想找出导致之后所有版本出错的第一个错误的版本。
你可以通过调用 bool isBadVersion(version) 接口来判断版本号 version 是否在单元测试中出错。实现一个函数来查找第一个错误的版本。你应该尽量减少对调用 API 的次数。
示例:
给定 n = 5,并且 version = 4 是第一个错误的版本。
调用 isBadVersion(3) -> false
调用 isBadVersion(5) -> true
调用 isBadVersion(4) -> true
所以,4 是第一个错误的版本。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/first-bad-version
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路
第一个二分查找的写法(向下取整)
public class Solution extends VersionControl {
public int firstBadVersion(int n) {
int left = 1;
int right = n;
while(left < right){
int mid = left + (right - left) / 2;
boolean x = isBadVersion(mid);
if(!x)
left = mid + 1;
if(x){
right = mid;
}
}
return left;
}
}
第 54 场双周赛
1893. 检查是否区域内所有整数都被覆盖
t题目描述
给你一个二维整数数组 ranges 和两个整数 left 和 right 。每个 ranges[i] = [starti, endi] 表示一个从 starti 到 endi 的 闭区间 。
如果闭区间 [left, right] 内每个整数都被 ranges 中 至少一个 区间覆盖,那么请你返回 true ,否则返回 false 。
已知区间 ranges[i] = [starti, endi] ,如果整数 x 满足 starti <= x <= endi ,那么我们称整数x 被覆盖了。
示例 1:
输入:ranges = [[1,2],[3,4],[5,6]], left = 2, right = 5
输出:true
解释:2 到 5 的每个整数都被覆盖了:
- 2 被第一个区间覆盖。
- 3 和 4 被第二个区间覆盖。
- 5 被第三个区间覆盖。
示例 2:
输入:ranges = [[1,10],[10,20]], left = 21, right = 21
输出:false
解释:21 没有被任何一个区间覆盖。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/check-if-all-the-integers-in-a-range-are-covered
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路
当时想到的就是排序,然后遍历,所有区间,找对应的值
但是刚开始我加了这么一句话,导致直接提交了三次都过不了,哭死!唉
if(left < ranges[0][0] || right > ranges[l - 1][1]) return false;
最后过的代码:
class Solution {
public boolean isCovered(int[][] ranges, int left, int right) {
Arrays.sort(ranges, new Comparator<int[]>(){
public int compare(int[] x, int[] y){
return x[1] == y[1] ? x[0] - y[0] : x[1] - y[1];
}
});
//或者用正则表达式
//Arrays.sort(ranges, (x, y) ->{
// return x[0] == y[0] ? x[1] - y[1] : x[0] - y[0];
//});
int index = 0;
int l = ranges.length;
while(left <= right){
if(left >= ranges[index][0] && left <= ranges[index][1])
left++;
else
index++;
if(index >= l)
break;
}
if(left > right)
return true;
else
return false;
}
}
说实话,题解的差分数组,没大看懂…
1894. 找到需要补充粉笔的学生编号
题目描述
一个班级里有 n 个学生,编号为 0 到 n - 1 。每个学生会依次回答问题,编号为 0 的学生先回答,然后是编号为 1 的学生,以此类推,直到编号为 n - 1 的学生,然后老师会重复这个过程,重新从编号为 0 的学生开始回答问题。
给你一个长度为 n 且下标从 0 开始的整数数组 chalk 和一个整数 k 。一开始粉笔盒里总共有 k 支粉笔。当编号为 i 的学生回答问题时,他会消耗 chalk[i] 支粉笔。如果剩余粉笔数量 严格小于 chalk[i] ,那么学生 i 需要 补充 粉笔。
请你返回需要 补充 粉笔的学生 编号 。
示例 1:
输入:chalk = [5,1,5], k = 22
输出:0
解释:学生消耗粉笔情况如下:
- 编号为 0 的学生使用 5 支粉笔,然后 k = 17 。
- 编号为 1 的学生使用 1 支粉笔,然后 k = 16 。
- 编号为 2 的学生使用 5 支粉笔,然后 k = 11 。
- 编号为 0 的学生使用 5 支粉笔,然后 k = 6 。
- 编号为 1 的学生使用 1 支粉笔,然后 k = 5 。
- 编号为 2 的学生使用 5 支粉笔,然后 k = 0 。
编号为 0 的学生没有足够的粉笔,所以他需要补充粉笔。
示例 2:
输入:chalk = [3,4,1,2], k = 25
输出:1
解释:学生消耗粉笔情况如下:
- 编号为 0 的学生使用 3 支粉笔,然后 k = 22 。
- 编号为 1 的学生使用 4 支粉笔,然后 k = 18 。
- 编号为 2 的学生使用 1 支粉笔,然后 k = 17 。
- 编号为 3 的学生使用 2 支粉笔,然后 k = 15 。
- 编号为 0 的学生使用 3 支粉笔,然后 k = 12 。
- 编号为 1 的学生使用 4 支粉笔,然后 k = 8 。
- 编号为 2 的学生使用 1 支粉笔,然后 k = 7 。
- 编号为 3 的学生使用 2 支粉笔,然后 k = 5 。
- 编号为 0 的学生使用 3 支粉笔,然后 k = 2 。
编号为 1 的学生没有足够的粉笔,所以他需要补充粉笔。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/find-the-student-that-will-replace-the-chalk
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路
这个题感觉比第一个题还简单,需要注意的就是用long防止溢出
class Solution {
public int chalkReplacer(int[] chalk, int k) {
int l = chalk.length;
int index = 0;
long sum = 0;
for(int i = 0; i < l; i++){
sum += chalk[i];
}
k = (int)((long)k % sum);
while(k >= chalk[index]){
k -= chalk[index];
index = index + 1;
}
return index;
}
}
1895. 最大的幻方
题目描述
一个 k x k 的 幻方 指的是一个 k x k 填满整数的方格阵,且每一行、每一列以及两条对角线的和 全部相等 。幻方中的整数 不需要互不相同 。显然,每个 1 x 1 的方格都是一个幻方。
给你一个 m x n 的整数矩阵 grid ,请你返回矩阵中 最大幻方 的 尺寸 (即边长 k)。
示例 1:
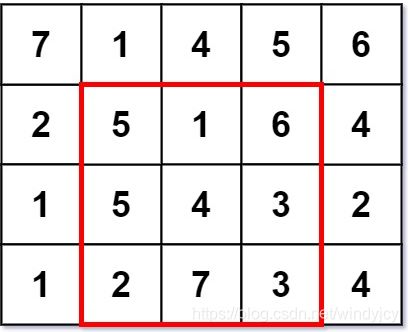
输入:grid = [[7,1,4,5,6],[2,5,1,6,4],[1,5,4,3,2],[1,2,7,3,4]]
输出:3
解释:最大幻方尺寸为 3 。
每一行,每一列以及两条对角线的和都等于 12 。
- 每一行的和:5+1+6 = 5+4+3 = 2+7+3 = 12
- 每一列的和:5+5+2 = 1+4+7 = 6+3+3 = 12
- 对角线的和:5+4+3 = 6+4+2 = 12
示例 2:
输入:grid = [[5,1,3,1],[9,3,3,1],[1,3,3,8]]
输出:2
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/largest-magic-square
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路
做了几次周赛了,我发现第三道题很喜欢出这种矩阵题…好像每次都有一道矩阵题
然后就是有思路,但是写不对…
我看了下数据范围,本来想处理每一行每一列的前缀和来着,后面觉得写的太麻烦,看了下数据范围,觉得暴力也能过,直接暴力吧,但是代码还是一直有问题,debug一下,看看问题出在哪里
当时代码:
class Solution {
int[][] grid;
int m;
int n;
public int largestMagicSquare(int[][] grid) {
//想了一会,觉得还不如之间遍历了
this.grid = grid;
int max = 1;
int len = m < n ? m : n;
//int[][] col = new int[m + 1][n + 1];
//int[][] row = new int[m + 1][n + 1];
//for(int i )
for(int i = 0; i < m; i++){
for(int j = 0; j < n; j++){
for(int k = max; k <= len; k++){
if(k == 1)
continue;
//这里应该写成>
if(i + k >= m || j + k >= n)
break;
if(judge(i, j, k))
max = Math.max(k, max);
}
}
}
return max;
}
public boolean judge(int i, int j, int k){
int value = 0;
//第i行的和
for(int y = j; y < j + k; y++){
value += grid[i][y];
}
//判断行和
for(int x = i + 1; x < i + k; x++){
int cur = 0;
for(int y = j; y < j + k; y++){
cur += grid[x][y];
}
if(cur != value)
return false;
}
for(int x = j; x < j + k; x++){
int cur = 0;
for(int y = i; y < i + k; y++){
cur += grid[y][x];
}
if(cur != value)
return false;
}
//对角线
int cox = 0;
for(int x = 0; x < k; x++){
cox += grid[i + x][j + x];
}
if(cox != value)
return false;
cox = 0;
for(int x = 0; x < k; x++){
//这里是i+k-1-x
cox += grid[i + k - x][j + x];
}
if(cox != value)
return false;
return true;
}
}
debug了一下,立马发现了问题,然后提交立马AC了…题解里也就是多处理了个前缀和…
说实话,挺难受的,每次都和做出第三道题插肩而过
改了以后的代码:
class Solution {
int[][] grid;
public int largestMagicSquare(int[][] grid) {
//想了一会,觉得还不如之间遍历了
this.grid = grid;
int m = grid.length;
int n = grid[0].length;
int max = 1;
int len = m < n ? m : n;
//int[][] col = new int[m + 1][n + 1];
//int[][] row = new int[m + 1][n + 1];
//for(int i )
for(int i = 0; i < m; i++){
for(int j = 0; j < n; j++){
for(int k = max; k <= len; k++){
if(k == 1)
continue;
if(i + k > m || j + k > n)
break;
if(judge(i, j, k))
max = Math.max(k, max);
}
}
}
return max;
}
public boolean judge(int i, int j, int k){
int value = 0;
//第i行的和
for(int y = j; y < j + k; y++){
value += grid[i][y];
}
//判断行和
for(int x = i + 1; x < i + k; x++){
int cur = 0;
for(int y = j; y < j + k; y++){
cur += grid[x][y];
}
if(cur != value)
return false;
}
for(int x = j; x < j + k; x++){
int cur = 0;
for(int y = i; y < i + k; y++){
cur += grid[y][x];
}
if(cur != value)
return false;
}
//对角线
int cox = 0;
for(int x = 0; x < k; x++){
cox += grid[i + x][j + x];
}
if(cox != value)
return false;
cox = 0;
for(int x = 0; x < k; x++){
cox += grid[i + k - 1 - x][j + x];
}
if(cox != value)
return false;
return true;
}
}
1896. 反转表达式值的最少操作次数
题目描述
给你一个 有效的 布尔表达式,用字符串 expression 表示。这个字符串包含字符 '1','0','&'(按位 与 运算),'|'(按位 或 运算),'(' 和 ')' 。
比方说,"()1|1" 和 "(1)&()" 不是有效 布尔表达式。而 "1", "(((1))|(0))" 和 "1|(0&(1))" 是 有效 布尔表达式。
你的目标是将布尔表达式的 值 反转 (也就是将 0 变为 1 ,或者将 1 变为 0),请你返回达成目标需要的 最少操作 次数。
比方说,如果表达式 expression = "1|1|(0&0)&1" ,它的 值 为 1|1|(0&0)&1 = 1|1|0&1 = 1|0&1 = 1&1 = 1 。我们想要执行操作将 新的 表达式的值变成 0 。
可执行的 操作 如下:
将一个 '1' 变成一个 '0' 。
将一个 '0' 变成一个 '1' 。
将一个 '&' 变成一个 '|' 。
将一个 '|' 变成一个 '&' 。
注意:'&' 的 运算优先级 与 '|' 相同 。计算表达式时,括号优先级 最高 ,然后按照 从左到右 的顺序运算。
示例 1:
输入:expression = "1&(0|1)"
输出:1
解释:我们可以将 "1&(0|1)" 变成 "1&(0&1)" ,执行的操作为将一个 '|' 变成一个 '&' ,执行了 1 次操作。
新表达式的值为 0 。
示例 2:
输入:expression = "(0&0)&(0&0&0)"
输出:3
解释:我们可以将 "(0&0)&(0&0&0)" 变成 "(0|1)|(0&0&0)" ,执行了 3 次操作。
新表达式的值为 1 。
示例 3:
输入:expression = "(0|(1|0&1))"
输出:1
解释:我们可以将 "(0|(1|0&1))" 变成 "(0|(0|0&1))" ,执行了 1 次操作。
新表达式的值为 0 。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/minimum-cost-to-change-the-final-value-of-expression
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路
当时没时间了,就看了个题,估计是动态规划
直接看注释吧,这题,我估计还得练个几百道才能在竞赛时间内做出来
class Solution {
//用一个二元组(x,y), 其中x表示将对应表达式的值变为 0,需要的最少操作次数,y 表示将对应表达式的值变为 1,需要的最少操作次数
Stack<int[]> num = new Stack<>(); //数字栈
Stack<Character> ops = new Stack<>(); //符号栈
public int minOperationsToFlip(String expression) {
for (int i = 0; i < expression.length(); i++) {
//当前字符
char c = expression.charAt(i);
//如果是数字
if (Character.isDigit(c)) {
//如果是0,那么
if (c == '0')
num.add(new int[]{0, 1});
else
num.add(new int[]{1, 0});
//如果是左括号
} else if (c == '(') {
ops.add('(');
//如果是右括号,进行计算
} else if (c == ')') {
while (ops.peek() != '(')
eval();
ops.pop();
//如果是符号&或者|,进行计算
} else {
while (!ops.isEmpty() && ops.peek() != '(')
eval();
ops.add(c);
}
}
while (!ops.isEmpty())
eval();
return Math.max(num.peek()[0], num.peek()[1]);
}
public void eval() {
//弹出当前运算符
int op = ops.pop();
//弹出栈顶的两个二元组
int[] b = num.pop();
int[] a = num.pop();
//如果是&,那么该怎么转移呢,只有1与1才是1
//所以s[0] = min{a[0] + b[0], a[0] + b[1], a[1] + b[0]}
//s[1] = a[1] + b[1]
//但是,还可以考虑将&转变成|,此时只需要一边为1就可以
//s[1] = min{s[1], a[1] + b[0] + 1, a[0] + b[1] + 1}
if (op == '&') {
int[] s0 = new int[]{b[0] + a[0], b[1] + a[0], b[0] + a[1]};
int[] s1 = new int[]{b[1] + a[1], b[1] + a[0] + 1, b[0] + a[1] + 1};
num.add(new int[]{get_min(s0), get_min(s1)});
//如果是|,那么该怎么转移呢,只有0|0才是0
//所以s[0] = a[0] + b[0]
//s[1] = min{a[1] + b[1], a[0] + b[1], a[1] + b[0]}
//但是,还可以考虑将|转变成&,此时只需要一边为0就可以
//s[0] = min{s[0], a[1] + b[0] + 1, a[0] + b[1] + 1}
} else {
int[] s0 = new int[]{b[0] + a[0], b[1] + a[0] + 1, b[0] + a[1] + 1};
int[] s1 = new int[]{b[1] + a[1], b[1] + a[0], b[0] + a[1]};
num.add(new int[]{get_min(s0), get_min(s1)});
}
}
private int get_min(int[] num) {
int min = Integer.MAX_VALUE;
for (int i = 0; i < num.length; i++) {
min = Math.min(min, num[i]);
}
return min;
}
}
第245场周赛
1897. 重新分配字符使所有字符串都相等
题目描述
给你一个字符串数组 words(下标 从 0 开始 计数)。
在一步操作中,需先选出两个 不同 下标 i 和 j,其中 words[i] 是一个非空字符串,接着将 words[i] 中的 任一 字符移动到 words[j] 中的 任一 位置上。
如果执行任意步操作可以使 words 中的每个字符串都相等,返回 true ;否则,返回 false 。
示例 1:
输入:words = ["abc","aabc","bc"]
输出:true
解释:将 words[1] 中的第一个 'a' 移动到 words[2] 的最前面。
使 words[1] = "abc" 且 words[2] = "abc" 。
所有字符串都等于 "abc" ,所以返回 true 。
示例 2:
输入:words = ["ab","a"]
输出:false
解释:执行操作无法使所有字符串都相等。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/redistribute-characters-to-make-all-strings-equal
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路
这个题做的时候,也出现了点小问题,脑子里想的是每个字符出现次数应该是数组长度的倍数,写的时候就去判断每个字符出现次数是否相同了。。。导致提交了三次才过
class Solution {
public boolean makeEqual(String[] words) {
//统计字符个数相同
int l = words.length;
if(l == 1)
return true;
int[] count = new int[26];
for(int i = 0; i < l; i++){
String s = words[i];
for(int j = 0; j < s.length(); j++){
count[s.charAt(j) - 'a']++;
}
}
for(int i = 0; i < 26; i++){
if(count[i] != 0 && count[i] % l != 0)
return false;
}
return true;
}
}
1898. 可移除字符的最大数目
题目描述
给你两个字符串 s 和 p ,其中 p 是 s 的一个 子序列 。同时,给你一个元素 互不相同 且下标 从 0 开始 计数的整数数组 removable ,该数组是 s 中下标的一个子集(s 的下标也 从 0 开始 计数)。
请你找出一个整数 k(0 <= k <= removable.length),选出 removable 中的 前 k 个下标,然后从 s 中移除这些下标对应的 k 个字符。整数 k 需满足:在执行完上述步骤后, p 仍然是 s 的一个 子序列 。更正式的解释是,对于每个 0 <= i < k ,先标记出位于 s[removable[i]] 的字符,接着移除所有标记过的字符,然后检查 p 是否仍然是 s 的一个子序列。
返回你可以找出的 最大 k ,满足在移除字符后 p 仍然是 s 的一个子序列。
字符串的一个 子序列 是一个由原字符串生成的新字符串,生成过程中可能会移除原字符串中的一些字符(也可能不移除)但不改变剩余字符之间的相对顺序。
示例 1:
输入:s = "abcacb", p = "ab", removable = [3,1,0]
输出:2
解释:在移除下标 3 和 1 对应的字符后,"abcacb" 变成 "accb" 。
"ab" 是 "accb" 的一个子序列。
如果移除下标 3、1 和 0 对应的字符后,"abcacb" 变成 "ccb" ,那么 "ab" 就不再是 s 的一个子序列。
因此,最大的 k 是 2 。
示例 2:
输入:s = "abcbddddd", p = "abcd", removable = [3,2,1,4,5,6]
输出:1
解释:在移除下标 3 对应的字符后,"abcbddddd" 变成 "abcddddd" 。
"abcd" 是 "abcddddd" 的一个子序列。
示例 3:
输入:s = "abcab", p = "abc", removable = [0,1,2,3,4]
输出:0
解释:如果移除数组 removable 的第一个下标,"abc" 就不再是 s 的一个子序列。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/maximum-number-of-removable-characters
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路
这个题,没想出来好吧,遍历还需要复杂度是n2,过不了
比赛结束第一时间看这道题,发现大佬们用的都是二分,瞬间明悟了,感觉没做出来实在不应该
class Solution {
public int maximumRemovals(String s, String p, int[] removable) {
//为什么能用二分查找呢,因为如果在removable数组中选择在s删除了前k个下标对应的字符,
//p仍然是s的子串的话,那么删除前k-1个下标,p肯定也是s的子序列
//因此具备二分性,可以用二分查找来降低复杂度
//首先需要写一个如何判断是子序列
//然后用每次删除对应的元素后的s,去匹配p
int l = removable.length;
int left = 0;
int right = l; //(要取到最后一个下标,需要是l)
while(left < right){
int mid = (right - left) / 2 + left;
StringBuffer sb = new StringBuffer(s);
//把该删除的字符删除掉
for(int i = 0; i <= mid; i++){
//注意:这里不能直接用deleteCharAt,而是替换
sb.setCharAt(removable[i], ' ');
}
if(check(sb.toString(), p)){
left = mid + 1;
}else
right = mid;
}
return left;
}
public boolean check(String s, String p){
int ls = s.length();
int lp = p.length();
int i = 0;
int j = 0;
while(i < ls && j < lp){
if(s.charAt(i) == p.charAt(j))
j++;
i++;
}
return j == lp;
}
}
1899. 合并若干三元组以形成目标三元组
题目描述
三元组 是一个由三个整数组成的数组。给你一个二维整数数组 triplets ,其中 triplets[i] = [ai, bi, ci] 表示第 i 个 三元组 。同时,给你一个整数数组 target = [x, y, z] ,表示你想要得到的 三元组 。
为了得到 target ,你需要对 triplets 执行下面的操作 任意次(可能 零 次):
选出两个下标(下标 从 0 开始 计数)i 和 j(i != j),并 更新 triplets[j] 为 [max(ai, aj), max(bi, bj), max(ci, cj)] 。
例如,triplets[i] = [2, 5, 3] 且 triplets[j] = [1, 7, 5],triplets[j] 将会更新为 [max(2, 1), max(5, 7), max(3, 5)] = [2, 7, 5] 。
如果通过以上操作我们可以使得目标 三元组 target 成为 triplets 的一个 元素 ,则返回 true ;否则,返回 false 。
示例 1:
输入:triplets = [[2,5,3],[1,8,4],[1,7,5]], target = [2,7,5]
输出:true
解释:执行下述操作:
- 选择第一个和最后一个三元组 [[2,5,3],[1,8,4],[1,7,5]] 。更新最后一个三元组为 [max(2,1), max(5,7), max(3,5)] = [2,7,5] 。triplets = [[2,5,3],[1,8,4],[2,7,5]]
目标三元组 [2,7,5] 现在是 triplets 的一个元素。
示例 2:
输入:triplets = [[1,3,4],[2,5,8]], target = [2,5,8]
输出:true
解释:目标三元组 [2,5,8] 已经是 triplets 的一个元素。
示例 3:
输入:triplets = [[2,5,3],[2,3,4],[1,2,5],[5,2,3]], target = [5,5,5]
输出:true
解释:执行下述操作:
- 选择第一个和第三个三元组 [[2,5,3],[2,3,4],[1,2,5],[5,2,3]] 。更新第三个三元组为 [max(2,1), max(5,2), max(3,5)] = [2,5,5] 。triplets = [[2,5,3],[2,3,4],[2,5,5],[5,2,3]] 。
- 选择第三个和第四个三元组 [[2,5,3],[2,3,4],[2,5,5],[5,2,3]] 。更新第四个三元组为 [max(2,5), max(5,2), max(5,3)] = [5,5,5] 。triplets = [[2,5,3],[2,3,4],[2,5,5],[5,5,5]] 。
目标三元组 [5,5,5] 现在是 triplets 的一个元素。
示例 4:
输入:triplets = [[3,4,5],[4,5,6]], target = [3,2,5]
输出:false
解释:无法得到 [3,2,5] ,因为 triplets 不含 2 。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/merge-triplets-to-form-target-triplet
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路
这个题做出来了,怎么想的呢,就是每次都是比较两个数组取较大值,因此必须得有三个数组(可以两个或者一个),三元组中一个元素等于target数组中对应的元素,其他两个小于target中对应元素
如果存在这样的“三个”数组,就可以形成target
class Solution {
public boolean mergeTriplets(int[][] triplets, int[] target) {
//想想,从左到右遍历,如果有一个包含目标数,并且后面
int l = triplets.length;
boolean flag1 = false;
boolean flag2 = false;
boolean flag3 = false;
for(int i = 0; i < l; i++){
if(triplets[i][0] == target[0] && triplets[i][1] <= target[1] && triplets[i][2] <= target[2])
flag1 = true;
if(triplets[i][1] == target[1] && triplets[i][0] <= target[0] && triplets[i][2] <= target[2])
flag2 = true;
if(triplets[i][2] == target[2] && triplets[i][0] <= target[0] && triplets[i][1] <= target[1])
flag3 = true;
}
if(flag1 && flag2 && flag3)
return true;
else
return false;
}
}
1900. 最佳运动员的比拼回合
题目描述
n 名运动员参与一场锦标赛,所有运动员站成一排,并根据 最开始的 站位从 1 到 n 编号(运动员 1 是这一排中的第一个运动员,运动员 2 是第二个运动员,依此类推)。
锦标赛由多个回合组成(从回合 1 开始)。每一回合中,这一排从前往后数的第 i 名运动员需要与从后往前数的第 i 名运动员比拼,获胜者将会进入下一回合。如果当前回合中运动员数目为奇数,那么中间那位运动员将轮空晋级下一回合。
例如,当前回合中,运动员 1, 2, 4, 6, 7 站成一排
运动员 1 需要和运动员 7 比拼
运动员 2 需要和运动员 6 比拼
运动员 4 轮空晋级下一回合
每回合结束后,获胜者将会基于最开始分配给他们的原始顺序(升序)重新排成一排。
编号为 firstPlayer 和 secondPlayer 的运动员是本场锦标赛中的最佳运动员。在他们开始比拼之前,完全可以战胜任何其他运动员。而任意两个其他运动员进行比拼时,其中任意一个都有获胜的可能,因此你可以 裁定 谁是这一回合的获胜者。
给你三个整数 n、firstPlayer 和 secondPlayer 。返回一个由两个值组成的整数数组,分别表示两位最佳运动员在本场锦标赛中比拼的 最早 回合数和 最晚 回合数。
示例 1:
输入:n = 11, firstPlayer = 2, secondPlayer = 4
输出:[3,4]
解释:
一种能够产生最早回合数的情景是:
回合 1:1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11
回合 2:2, 3, 4, 5, 6, 11
回合 3:2, 3, 4
一种能够产生最晚回合数的情景是:
回合 1:1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11
回合 2:1, 2, 3, 4, 5, 6
回合 3:1, 2, 4
回合 4:2, 4
示例 2:
输入:n = 5, firstPlayer = 1, secondPlayer = 5
输出:[1,1]
解释:两名最佳运动员 1 和 5 将会在回合 1 进行比拼。
不存在使他们在其他回合进行比拼的可能。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/the-earliest-and-latest-rounds-where-players-compete
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路
看注释吧,不太好理解
还可以用记忆化搜索进行优化,也就是用dp[n][f][s][2]将,当前n个人,并且两个最佳运动员位置在f和s,最少回合数和最多回合数
class Solution {
//首先明确,如果f+s == n+1 ,就说明两个人相遇了
//f 对称的位置是 f' = n + 1 - f;s对称的位置是s' = n + 1 - s
//而考虑两个最佳运动员的位置,因为两个最佳运动员的位置可以互换,并不会影响最后的结果,
//所以,只考虑 f 离左边的距离小于 s 离右边的距离 的情况
public int[] earliestAndLatest(int n, int firstPlayer, int secondPlayer) {
if (firstPlayer + secondPlayer == n + 1){
return new int[]{1,1};
}
//如果f 离左边的距离大于 s 离右边的距离了,那么就将这两个人的相对位置进行互换,不影响结果
if (firstPlayer > n + 1 - secondPlayer){
return earliestAndLatest(n, n + 1 - secondPlayer, n + 1 - firstPlayer);
}
int m = (n + 1) >> 1; //中间位置,也就是下一轮剩下的人数,向上取整
int min = n, max = 0;
//如果两个运动员都在同一侧(或者s在中间),f 左边有f−1个运动员,那么进行一轮比赛以后,可能留下 0~f-1 个人,所以fx的位置就可能是1到f
//f到s之间有s - f - 1个运动员,结束以后,可能剩下0~s-f-1个运动员,所以sx的位置,就是 fx + 1 ~ s- f- 1 + fx + 1
//遍历所有可能出现的情况,最早回合数就是取最小值,最晚回合数就是取最大值
if (secondPlayer <= m){
for (int f = 1; f <= firstPlayer; f++) {
for (int s = f + 1; s <= secondPlayer - firstPlayer + f; s++) {
int[] el = earliestAndLatest(m, f, s);
min = Math.min(el[0], min);
max = Math.max(el[1], max);
}
}
//如果f和s在两侧,s的对称位置就是s' = n + 1 - s
//与上一种情况同理,f左边情况一样
//f到s'出现的人数也与上一种情况一样,
//s'到s出现的人数,因为是对称的,所以不论怎么比,都是出现m - s' - 1个人(即一半人)
//所以下一轮s的位置sx,就是在上一种情况的基础上(以s'为s的情况下),再加上中间出现的人数,也就是m - s' - 1,再加1
//就有下面这种转移方程
}else {
int _s = n + 1 - secondPlayer;
for (int f = 1; f <= firstPlayer; f++) {
for (int s = f + 1; s <= _s - firstPlayer + f ; s++) {
int[] el = earliestAndLatest(m, f, s + m - _s);
min = Math.min(el[0],min);
max = Math.max(el[1],max);
}
}
}
//最后的结果,加上当前轮次
return new int[]{min + 1, max + 1};
}
}
记忆化搜索的代码:
class Solution{
int[][][][] earliest = new int[28][28][28][2];
public int[] earliestAndLatest(int n, int fp, int sp) {
if (earliest[n][fp][sp][0] != 0) return earliest[n][fp][sp];
if (sp == n-fp+1) {
earliest[n][fp][sp][0] = earliest[n][fp][sp][1] = 1;
return earliest[n][fp][sp];
}
solveEar(n ,fp, sp, 1, new boolean[n+1]);
return earliest[n][fp][sp];
}
public void solveEar(int n, int fp, int sp, int index, boolean[] se) {
int s = n-index+1;
if (index >= s) {
if (index == n-index+1) se[index] = true;
int nfp = 0, nsp = 0;
for (int i = 1; i <= n; i++) {
if (i <= fp && se[i]) nfp++;
if (i <= sp && se[i]) nsp++;
}
int[] ints = earliestAndLatest(n / 2 + (n % 2), nfp, nsp);
if (earliest[n][fp][sp][0] == 0 || earliest[n][fp][sp][0] > ints[0]+1)
earliest[n][fp][sp][0] = ints[0]+1;
if (earliest[n][fp][sp][1] == 0 || earliest[n][fp][sp][1] < ints[1]+1)
earliest[n][fp][sp][1] = ints[1]+1;
return;
}
if (s != fp && s != sp) {
se[index] = true; se[s] = false;
solveEar(n, fp, sp, index+1, se);
}
if (index != sp && index != fp) {
se[index] = false; se[s] = true;
solveEar(n, fp, sp, index+1, se);
}
}
}
作者:god_like
链接:https://leetcode-cn.com/problems/the-earliest-and-latest-rounds-where-players-compete/solution/ji-yi-hua-sou-suo-by-god_like-ftpd/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
小结
这周两个周赛,周六晚上的还好,周日是真没太想做,但是想着做了一个另一个不做,那积分不是拿不到了么,有点亏哈哈,所以还是坚持着把周日的也做了,虽然做了半个来小时做不出来剩下的就算了,但这也算一种精神上的进步吧哈哈
这两次周赛怎么说呢,好像还是没有什么进步,第三道题依旧是思路拉满,但是代码一写就有小毛病,而且第一道题还会错好几次。挺难受的,其实看了一下,两道题如果不错按我的速度做出来不错的话,1000名之内还是没问题的,第三道再认真一点,可能也能做出来
至于最后一道题呢,每次基本上都是动规了,各种各样的动规,想起来确实费脑筋。今天偶然看到一个帖子,做了二百道题,什么周赛只能过两道什么什么的,我一想我已经刷了将近500道了,然后还是过两道的水平…瞬间有点小难受,可能还是自己太菜了,还要加油啊
总结完毕,又得搞课题了,-_-