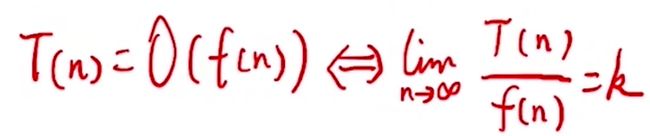数据结构总结——第一章
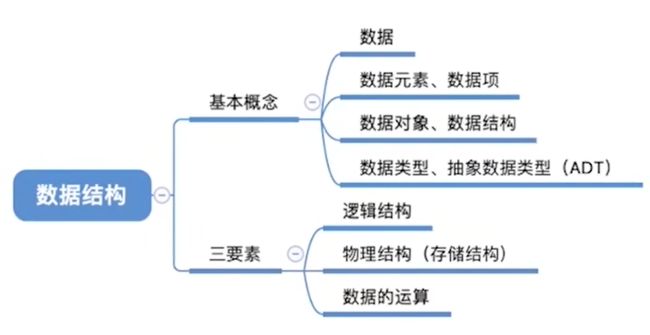
1.1数据结构
数据的基本单位是数据元素。
通常把数据元素作为一个整体进行处理。
sometime一个数据元素可以由若干个数据项(也可称为字段、域、属性)组成。
数据对象:具有相同类型(性质)的数据元素的集合。
数据项:具有独立意义的不可分割的最小标识单位。
数据结构:是互相之间存在一种或多种特定关系的数据元素的集合。(强调元素之间的结构)
数据结构:带结构的数据元素的集合。
1.1.1逻辑结构
数据元素之间的逻辑关系的整体称为数据的逻辑结构;
- 集合:包含的所有数据元素同属于一个集合(数据元素之间没有关系,集合是一种最松散的罗逻辑结构)
- 线性结构:包含的数据元素之间存在一对一的关系。
- 树状结构:包含的数据元素之间存在一对多的关系。
- 图状结构:包含的数据元素之间存在多对多的关系。
二元组 : 常用/通用的数据逻辑结构表示方式。
eg:S=(D,R) ()表示无向关系,如(a,b)表示既存在元素a到b之间的关系,又存在元素b到a之间的关系
D={di|1<=i<=n} {}表示有向关系,如{a,b}表示元素a到b之间的关系。
R={rj|1<=j<=m}
D 是数据元素的有限集合,即D是由有限个数据元素所构成的集合。
R 是D上的关系的有限集合,即R是由有限个关系rj所构成的集合。
若不存在一个d'使
若不存在一个d'使
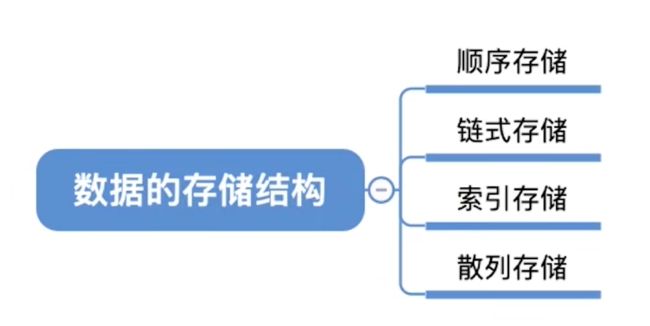
1.1.2.存储结构(物理结构)
数据逻辑结构在计算机存储器中的表示称为数据的存储结构(存储表示)/物理结构。
同一种逻辑结构可以设计多种存储结构,在不同的存储结构中,实现同一种运算的算法可能不同。
- 顺序存储结构:顺序存储结构采用一组连续的存储单元存放所有的数据元素,且逻辑上相邻的元素的存储单位也相邻。。即顺序存储结构将数据结构直接映射到存储结构。
优点:节省存储空间 因为分配的数据的存储单元全用于存放元素值,元素之间逻辑关系的表示没有占用额外的存储空间。
缺点:不便于修改,在进行元素的插入、删除运算时,可能要移动一系列元素。
- 链式存储结构:每个结点单独存储,无须占用一整块存储空间,但为了表示结点间的关系,给每个结点附加指针字段,用于存放相邻结点的存储地址。
优点:便于修改,在进行元素的插入、删除运算时,仅需要修改结点的指针域,不需要移动结点。
缺点:存储空间利用率低,因为分配给数据元素的存储单元一部分用于存放结点之间逻辑关系了。
ps:由于逻辑上相邻的结点在存储器上比一定相邻,so在用这种方法存储的线性结构中不能对结点随机存取。
- 索引存储结构:索引存储结构是在存储数据(主数据表)的同时,还建立附加的索引表。索引表的每一项称为索引项。
优点:查找率高
缺点:需要建立索引表,增加了时间和空间开销。
- 哈希(散列)存储结构:根据元素的关键字来确定其存储地址。
做法:以元素的关键字为自变量,通过某个哈希函数计算出对应的函数值,再把该函数值当作该元素的存储地址。
优点:查找速度快,给关键字,计算存储地址。
缺点:只存储数据元素本身,不存储元素之间的逻辑关系。
1.1.3数据运算
数据运算就是施加于数据的操作。
选用好的存储结构可以提高运算实现的效率。
1.2算法和算法分析
1.2.1算法的基本概念
算法是指令的有限序列。
算法是对特定问题求解步骤的一种描述。
一个运算实现是通过算法来表述的。
1.2.2算法分析
1.2.2.1算法时间复杂度分析
算法的执行时间主要与问题规模有关。
频度:指该语句在算法中被重复执行的次数,算法中所有语句的频度之和记作T(n),T(n)与算法的执行时间成正比。
当问题规模n趋向无穷大时,T(n)的数量级称为渐进时间复杂度,简称时间复杂度,记作T(n)=O(f(n))。
即当n趋近于无穷大时,可以只考虑高阶部分,eg:f=n3+3约等于O(n3).
T(时间开销)
n(问题规模)
常对幂指阶
即常数小于对数小于幂数小于指数小于阶乘————常数最稳定
结论
1.顺序执行的代码只会影响常数项,可以忽略。——即顺序语句只会增加常数项--最终都约等于1.
2.只需挑循环语句中的一个基本操作分析它的执行次数与n的关系即可。
3.如果有多层嵌套循环,则只用关注最深层循环循环了几次
例题:
一般只考虑最坏情况和平均情况。
总结
1.2.2.2算法空间复杂度分析
一个算法的存储量包括形参所占的空间和临时变量所占的空间.......
空间复杂度是对一个算法在运行过程中临时占用的存储空间大小的量度,一般也作为问题规模n的函数,以数量级的形式给出,记作:S(n)=O(g(n))。
算法的空间复杂度的计算同时间复杂度
1.3数据结构程序设计
1.3.1数据结构程序设计步骤
第一步:分析求解问题的数据和求解功能,采用抽象数据类型来描述求解问题,主要包括数据逻辑结构和运算定义。
第二步:设计逻辑结构对应的存储结构。(关键)
第三步:在存储结构上设计实现运算定义的算法。
ps:此三步不是独立的,因为不可能设计出一大堆算法后再从中找出一个好的算法,一个好的算法很大程度上取决于描述实际问题的存储结构,so必须以设计好算法为目标来设计存储结构,因为数据存储结构会影响算法的好坏。设计好的存储结构可以提高算法的效率。
概括:求解问题的一般步骤————建立其抽象数据类型,针对算法的实现设计出合理的存储结构,在此基础上设计尽可能高效的算法。
1.3.2应用程序的结构
章结:
- 算法满足有限性,程序不一定满足有限性。算法可以直接用计算机程序来描述,但算法必须用程序设计语言来描述是错误的。
- 在设计算法时,要弄清哪些是算法输入,哪些是要求解的结果即算法输出,通常将他们设计成函数形参,求解的结果可以作为引用型参数或函数返回值。
- 描述一个问题的抽象数据类型由数据逻辑结构和抽象运算组成。
- 对于一个算法给定的条件,需要判断其有效性,通常当条件有效并正确执行时返回1(真),否则返回0(假)。
- 算法分析包含时间复杂度和空间复杂度分析,其目的是分析算法的效率 以求改进。
- 在分析算法时间复杂度时,通常选取算法中的基本运算,求出其频度,取最高阶并置系数为1作为该算法的时间复杂度。
- 线性结构中数据元素之间是一对一关系。
- 数据结构中与计算机无关的是数据的逻辑结构。 因为数据的逻辑结构只抽象的反应数据元素之间的逻辑关系,而不管它在计算机中的存储表示形式。逻辑结构从逻辑关系上描述数据,与数据的存储无关,是独立于计算机的。
- 在计算机存储数据时,通常不仅要存储各数据元素的值,还有存储数据元素之间的关系。
- 数据采用链式存储结构时,要求每个节点占用一片连续的存储区域。
- 计算机所处理的数据一般具备某种内在联系,这里指元素与元素之间存在某种关系。
- 数据结构在计算机内存中的表示是指数据的存储结构。
- 可以用抽象数据类型定义一个完整的数据结构。
- 计算机的算法指求解问题的有限运算数列。
- 在算法设计时,若实参和形参同步发生改变,则应把形参变量说明为引用型参数。