01神经网络的理论及实现
感知机的缺点就是需要设置合适的权重,而权重的设置都是人工操作的。
1、从感知机到神经网络
重新画出感知机的模型,在图上加上偏置,由于偏置始终为1,所以颜色加深。
图1-1 感知机模型
引入新函数(激活函数):
将感知机表达式改为:
![]() (1-2)
(1-2)
也可以分开写为:
![]() (1-3)
(1-3)
![]() (1-4)
(1-4)
根据公式(1-3)和(1-4)可以将图1-1更改为图1-2模型。
图1-2 加入激活函数的感知机图
2、激活函数
激活函数会将输入信号的总和转换为输出信号。
激活函数如果使用阶跃函数,就是感知机。
如果使用其它激活函数,就是神经网络。
2.1 阶跃函数
公式(1-1)就是阶跃函数。
实现代码:
import numpy as np
import matplotlib.pylab as plt
def step_function(x):
return np.array(x>0,dtype=int)
x=np.arange(-5,5,0.1)
y=step_function(x)
plt.plot(x,y)
plt.ylim(-0.1,1.1)
plt.show()运行结果:
原来的程序运行出错:
AttributeError: module 'numpy' has no attribute 'int'
解决办法:是因为版本的问题,将dtype=np.int更改为dtype=int即可。
2.2 sigmoid函数
Sigmoid型函数是一类S型曲线函数,为两端饱和函数,常见的有Logistic函数和Tanh函数。
饱和:
对于函数f(x),若![]() 时,导数
时,导数![]() ,称为左饱和,当
,称为左饱和,当![]() 时,导数
时,导数![]() ,称为右饱和。两个都满足的情况下称为两端饱和。
,称为右饱和。两个都满足的情况下称为两端饱和。
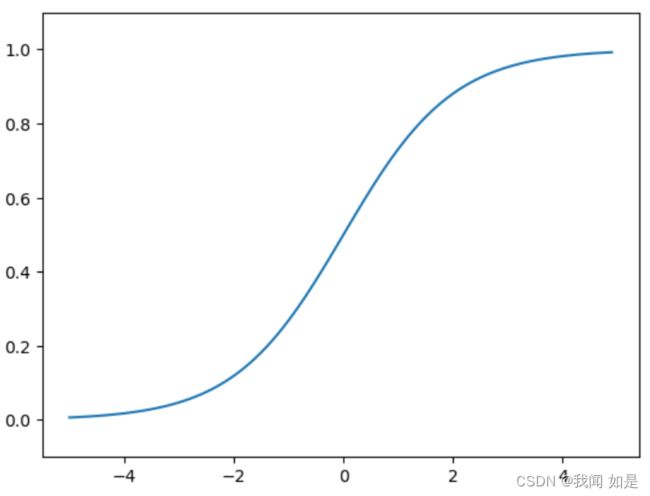
2.2.1 Logistic函数
表达式:
![]() (1-5)
(1-5)
实现代码:
def sigmoid(x):
return 1/(1+np.exp(-x))
x=np.arange(-5,5,0.1)
y=sigmoid(x)
plt.plot(x,y)
plt.ylim(-0.1,1.1)
plt.show()输出:
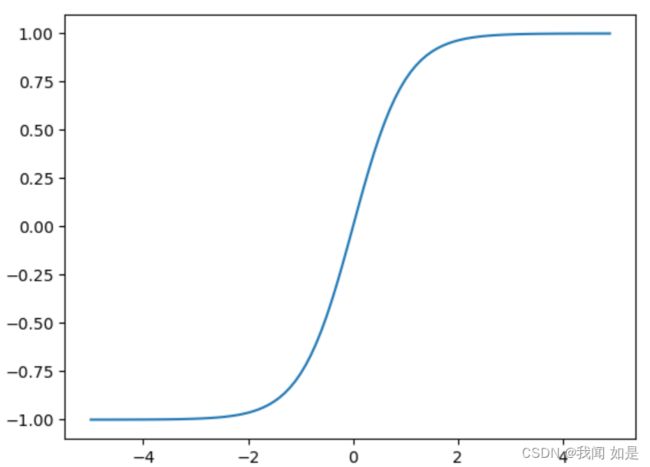
2.2.2 Tanh函数
表达式:
![]() (1-6)
(1-6)
实现代码:
def tanh(x):
return (np.exp(x)-np.exp(-x))/(np.exp(x)+np.exp(-x))
x=np.arange(-5,5,0.1)
y1=tanh(x)
plt.plot(x,y1)
plt.ylim(-1.1,1.1)
plt.show()输出:
Tanh函数的输出是零中心化的,而Logistic函数的输出恒大于0。非中心化的输出会使得其后一层的神经元的输入发生偏置偏移,并进一步使得梯度下降的收敛速度变慢。
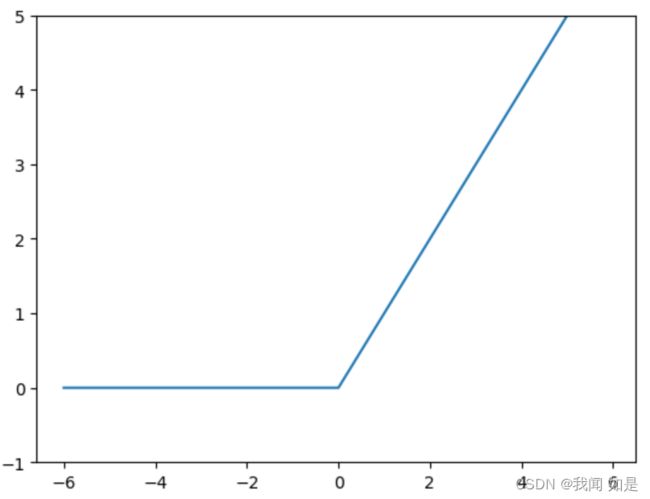
2.3 ReLU函数
ReLU(Rectified Linear Unit)函数,表达式为:
实现代码:
def relu(x):
return np.maximum(0,x)
x=np.arange(-6,6,0.1)
y=relu(x)
plt.plot(x,y)
plt.ylim(-1,5)
plt.show()输出:
优点:
1、只需要进行加、乘和比较的操作,计算更高效。
2、具有很好的稀疏性,大约50%的神经元处于激活状态。
3、具有左饱和函数,在一定程度上缓解了梯度消失问题,加速梯度下降的收敛速度。
缺点:
1、非零中心化,影响梯度下降的效率;
2、死亡ReLU问题,即一次不恰当的更新后,ReLU神经元都不能被激活,永远可能都会是0.
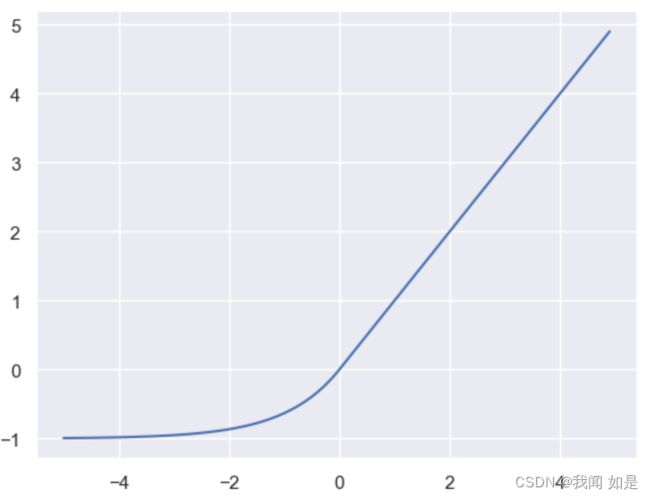
2.3.1 带泄露的ReLU(Leaky ReLU)
在x<0时,可以保持一个很小的梯度![]() ,避免死亡ReLU的问题。
,避免死亡ReLU的问题。
表达式:
![]() 一般选择为0.01.
一般选择为0.01.
代码实现:
import numpy as np
import matplotlib.pyplot as plt
def Leaky_relu(x):
return np.maximum(0.01*x,x)
x=np.arange(-5.0,5.0,0.1)
y=Leaky_relu(x)
plt.plot(x,y)
plt.show()输出:
和ReLU相比,负方向有个很小的弧度。
2.3.2 带参数的ReLU
带参数的ReLU(parametric ReLU,PReLU),PReLU是一个参数可变的函数。
表达式:
2.3.3 ELU函数
ELU(Exponential Linear Unit,指数线性单元)
定义:
代码实现:
import numpy as np
import matplotlib.pyplot as plt
import math
def elu(x,alpha=1):
a = x[x>0]
b = alpha*(math.e**(x[x<0])-1)
result=np.concatenate((b,a),axis=0)
return result
x=np.arange(-5.0,5.0,0.1)
y=elu(x)
plt.plot(x,y)
plt.show()输出:
3、3层神经网络的实现
代码实现:
def init_network():#初始化权重和偏置
network={}
network['W1']=np.array([[0.1,0.3,0.5],[0.2,0.4,0.6]])
network['b1']=np.array([0.1,0.2,0.3])
network['W2']=np.array([[0.1,0.4],[0.2,0.5],[0.3,0.6]])
network['b2']=np.array([0.1,0.2])
network['W3']=np.array([[0.1,0.3],[0.2,0.4]])
network['b3']=np.array([0.1,0.2])
return network
def forward(network,x):#前向传递,封装将输入信号转换为输出信号的处理过程
W1,W2,W3=network['W1'],network['W2'],network['W3']
b1,b2,b3=network['b1'],network['b2'],network['b3']
a1=np.dot(x,W1)+b1
z1=sigmoid(a1)
a2=np.dot(z1,W2)+b2
z2=sigmoid(a2)
a3=np.dot(z2,W3)+b3
y=identity_function(a3)
return y
network=init_network()
x=np.array([1,0.5])
y=forward(network,x)
y输出:
array([0.31682708, 0.69627909])
4、softmax函数
表达式:
![]() (1-11)
(1-11)
由于会出现溢出情况,所以将公式(1-11)变换。
(1-12)
为了防止溢出,增加![]() 为任何值,一般会使用输入信号中的最大值。
为任何值,一般会使用输入信号中的最大值。
实现代码:
def softmax(a):
c=np.max(a)
exp_a=np.exp(a-c)
sum_exp_a=np.sum(exp_a)
y=exp_a/sum_exp_a
return ysoftmax函数的输出是0~1.0之间的实数,总和为1。所以才把softmax函数的输出解释为“概率”。
举例:
a=np.array([0.3,2.9,4])
y=softmax(a)
y输出:
array([0.01821127, 0.24519181, 0.73659691])
可以解释为y[0]概率0.018(1.8%),y[1]概率为0.245(24.5%),y[2]概率为0.737(73.7%)。
从概率结果可以看出,有74%概率是第2个类别。
由于指数函数的运算需要一定的计算机运算量,因此输出层的softmax函数一般会被省略。
5、手写数字识别实例
和机器学习步骤一样,分为学习和推理两个阶段。学习就是首先使用训练数据进行权重参数的学习;然后进行推理,使用刚才学习到的参数,对输入参数进行分类。
minist 显示代码
# coding: utf-8
import sys, os
sys.path.append(os.pardir) # 为了导入父目录的文件而进行的设定
import numpy as np
from dataset.mnist import load_mnist
from PIL import Image
def img_show(img):
pil_img = Image.fromarray(np.uint8(img))
pil_img.show()
(x_train, t_train), (x_test, t_test) = load_mnist(flatten=True, normalize=False)
img = x_train[0]
label = t_train[0]
print(label) # 5
print(img.shape) # (784,)
img = img.reshape(28, 28) # 把图像的形状变为原来的尺寸
print(img.shape) # (28, 28)
img_show(img)输出第1个图片:
计算精度的程序:
# coding: utf-8
import sys, os
sys.path.append(os.pardir) # 为了导入父目录的文件而进行的设定
import numpy as np
import pickle
from dataset.mnist import load_mnist
from common.functions import sigmoid, softmax
def get_data():
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, flatten=True, one_hot_label=False)
return x_test, t_test
def init_network():
with open("sample_weight.pkl", 'rb') as f:
network = pickle.load(f)
return network
def predict(network, x):
W1, W2, W3 = network['W1'], network['W2'], network['W3']
b1, b2, b3 = network['b1'], network['b2'], network['b3']
a1 = np.dot(x, W1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1, W2) + b2
z2 = sigmoid(a2)
a3 = np.dot(z2, W3) + b3
y = softmax(a3)
return y
x, t = get_data()
network = init_network()
accuracy_cnt = 0
for i in range(len(x)):
y = predict(network, x[i])
p= np.argmax(y) # 获取概率最高的元素的索引
if p == t[i]:
accuracy_cnt += 1
print("Accuracy:" + str(float(accuracy_cnt) / len(x)))输出精度为:93.51%。
5.1 批处理
# coding: utf-8
import sys, os
sys.path.append(os.pardir) # 为了导入父目录的文件而进行的设定
import numpy as np
import pickle
from dataset.mnist import load_mnist
from common.functions import sigmoid, softmax
def get_data():
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, flatten=True, one_hot_label=False)
return x_test, t_test
def init_network():
with open("sample_weight.pkl", 'rb') as f:
network = pickle.load(f)
return network
def predict(network, x):
w1, w2, w3 = network['W1'], network['W2'], network['W3']
b1, b2, b3 = network['b1'], network['b2'], network['b3']
a1 = np.dot(x, w1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1, w2) + b2
z2 = sigmoid(a2)
a3 = np.dot(z2, w3) + b3
y = softmax(a3)
return y
x, t = get_data()
network = init_network()
batch_size = 100 # 批数量
accuracy_cnt = 0
for i in range(0, len(x), batch_size):
x_batch = x[i:i+batch_size]
y_batch = predict(network, x_batch)
p = np.argmax(y_batch, axis=1)
accuracy_cnt += np.sum(p == t[i:i+batch_size])
print("Accuracy:" + str(float(accuracy_cnt) / len(x)))参考资料:
1、深度学习入门:基于python的理论与实现
2、神经网络与深度学习 邱锡鹏。