中等题 ------ 数组以及字符串
以前刷的都是一些简单题,从一些基本的数据结构到算法,得有400多道了,简单题就先这样吧,从今天以后就开始着手中等题和困难题了。
做了一些中等题,感觉确实和简单题没法比,简单题有些直接模拟,暴力就能做出来,而这些中等题是根本想不到该怎么做,但看了题解,找到公式关系,规律也就觉得还行,慢慢加油吧。
本篇是一些关于数组和字符串的题。
数组和字符串的简单题在这。
文章目录
- 1. 数组嵌套
- 2. 非递减数列
- 3. 最佳观光组合
- 4. 对角线遍历
- 5. 生命游戏
- 5. 分割数组
- 6. 找出数组游戏的赢家
- 7.除自身以外数组的乘积
- 8. 旋转函数
- 9. 旋转图像
- 10.递增三元子序列
-
- (1)两次遍历
- (2)贪心
- 11. 优美的排列
- 12.盛最多水的容器
- 13. 三数之和
- 14.下一个排列
- 15. Z 字形变换
- 16. 验证IP地址????(可以不看,本人的痛苦回忆)
- 17. 破坏回文串
- 18. 竖直打印单词
- 19.在LR字符串中交换相邻字符
- 20. 情感丰富的文字
- 21.字符串转换整数(atoi)
- 22. HTML实体解析器
- 23.无重复的字串
- 24. 最长回文子串
-
- (1)暴力美学(YYDS!!)
- (2)动态规划
- (3)双指针(中心扩散)
- 25.整数转罗马数字
- 26. 电话号码的字母组合
- 27.外观数列
- 28.编辑距离
- 29.解码方法
- 30. 交错字符串
1. 数组嵌套

这道题的意思就是说你嵌套的去访问,直接模拟题目的意思,看看那一个的长度最长就好了。
测试用例所给的S[0],模拟出其他的S[1~6]这都是可以模拟出来的,但是会超出时间限制。
需要一些技巧,将其转化成图的形式更直观一点,你会发现这个图是,一个带多个环的图,选出其中环顶点最多的那一个就好了,而遍历图的精髓则在于那一个Vist数组标记着当前顶点是否访问过。
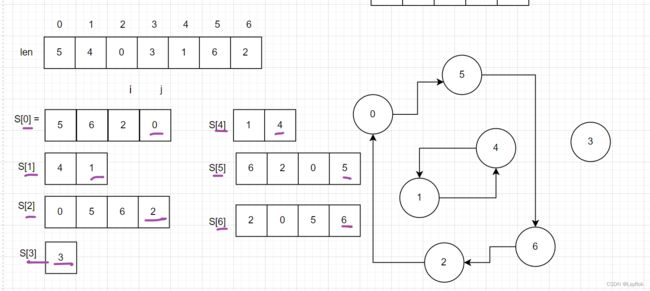
- 创建一个visit数组来标识该顶点是否访问过。
- 然后在遍历数组,如果没访问过,循环与他有关的顶点,同时将其相关的顶点也加入到Vist数组中去。
int Max(int x, int y)
{
return x > y ? x : y;
}
int arrayNesting(int* nums, int numsSize)
{
int i,maxLen = 1;
int* visit = (int*)calloc(numsSize,sizeof(int));
for (i = 0; i < numsSize; i++)
{
//访问过直接返回就好了
if(visit[i] == 1)
{
continue;
}
visit[i] = 1;
int j = nums[i], len = 1;
//未访问过的
while(visit[j] != 1)
{
len++;
visit[j] = 1;
j = nums[j];
}
maxLen = Max(maxLen,len);
}
return maxLen;
}
2. 非递减数列

这道题的意思就是说,你可以修改数组中的一个数,但要保证修改完后,可以是非递减的数列,比如这两者种序列: 1 2 3 4 和1 1 2 3都属于非递减数列。
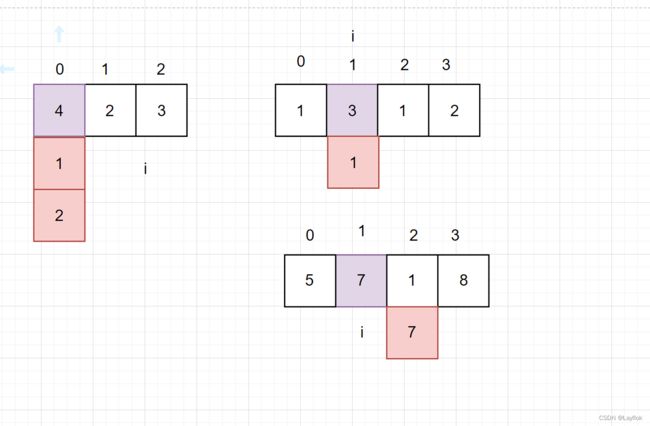
看下图种,要想一个数列是递增的,i所指向的数如果大于下一个数,就说明称递减了。
所以我们就要对其进行修改,下面是三种情况,其实仔细看看会发现,第一种情况它可以将4修改为1或者是2都没有关系,而官方给的是修改成1,让他变成1 2 3这一个数列。
又因为他是要改变为非递增的,所以说分为右边的两种情况:
- nums[i - 1] <= nums[i + 1] 使nums[i] = nums[ i + 1]
- nums[i - 1] > nums[i + 1] 使nums[i + 1] = nunm[i]
- 而对于边界0下标来说,不管将自己改成哪一种?都不会影响最后的结果。
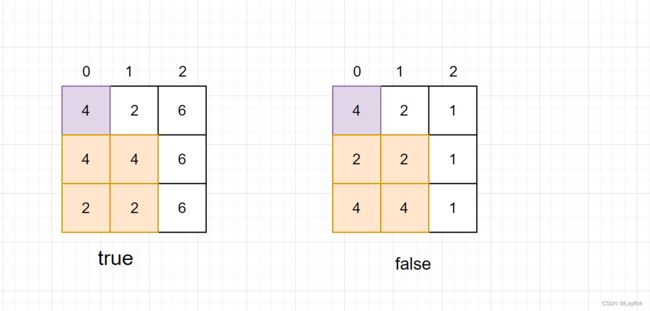
而将i的位置就该后,如果还出现递减的情况,就说明修改一次不行,返回false就好了
bool checkPossibility(int* nums, int numsSize)
{
int i,count = 0;
for (i = 0; i < numsSize - 1; i++)
{
//发现递减时候
if(nums[i] > nums[i + 1])
{
count++;
if(i > 0 && nums[i - 1] > nums[i + 1])
{
nums[i + 1] = nums[i];
}
else
{
nums[i] = nums[i + 1];
}
}
}
return count < 2;
}
3. 最佳观光组合

这道题就题目中已经给出公式,要求出values[i] + values[j] + i - j 的最大值。
使用暴力双for肯定是会超时的,所以得进行优化。
下面是leetcode官方的题解,转换式子拿一下确实妙啊。
- values[i] + values[j] + i - j 可以变成 values[i] + i + valuse[j] - j 的形式
- 我们可以直接拿一个变量 max 来存储 values[i] + i 的值,
- 这样就变成了一个max + valuse[j] - j 的形式(妙。。)
- 这样子的话,i全部在一起,j全部在一起,就可以通过遍历一遍来实现。
注意一定是先去求答案,再去维护最大值,就会算出自己+自己情况,那样子是错的。
int maxScoreSightseeingPair(int* values, int valuesSize)
{
int i = 0,j,max = values[0],ans = max;
for (j = 1; j < valuesSize;j++)
{
//先去求ans
if(max + values[j] - j > ans)
{
ans = max + values[j] - j;
}
//再去维护最大值
if(values[j] + j > max)
{
max = values[j] + j;
}
}
return ans;
}
4. 对角线遍历
这道题的意思就是让你看图片,懂了吗?不行再看下一张,ok了不?
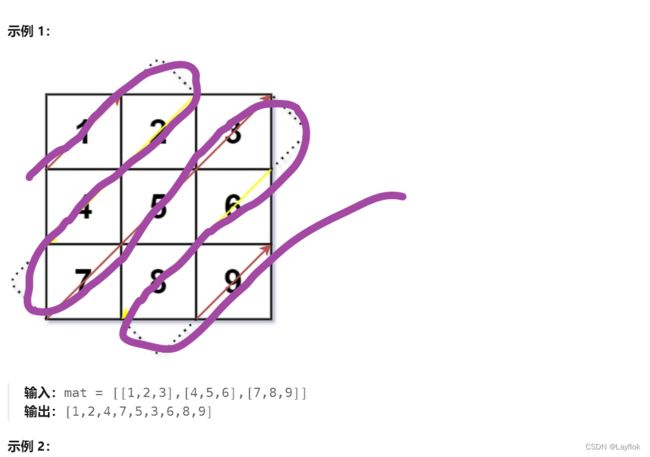
- 首先先看普通情况,就是说如果右上走的话:x--,y++.左下走的话使x++,y--;
- 但是要注意边界条件,上下左右四个边界条件。
- 上下:如果x == 0 || x == row - 1了,再动就出界了,只需要将y++即可。
- 左右:如果y == 0 || y == col - 1,那么肯定是x++;
移动能移动了,还需要判断它往那个方向移动。
- (x + y) % 2 偶数向右上移动,奇数向左下移动。
/**
* Note: The returned array must be malloced, assume caller calls free().
*/
int* findDiagonalOrder(int** mat, int matSize, int* matColSize, int* returnSize)
{
int size = matSize * matColSize[0];
int* ans = (int*)malloc(sizeof(int) * size);
*returnSize = size;
int index = 0;
int row = matSize, col = matColSize[0];
int x = 0, y = 0;
while(index < size)
{
ans[index++] = mat[x][y];
if ((x + y) % 2 == 0)
{
//右上方去遍历
if(y < col - 1)
{
y++;
if(x > 0)
{
x--;
}
}
else
{
x++;
}
}
else
{
//往左下方去遍历
if(x < row - 1)
{
x++;
if(y > 0)
{
y--;
}
}
else
{
y++;
}
}
}
return ans;
}
5. 生命游戏

这道题的意思是统计出自身周围8个位置(以自身为坐标9宫格)有多个活着的细胞也就是1,判断那四种生存定律就好了。
int GetLive(int** board, int row, int col, int x, int y)
{
int coordX[8] = {-1,-1,-1,0,1,1,1,0};
int coordY[8] = {-1,0,1,1,1,0,-1,-1};
int i,count = 0;
for (i = 0; i < 8; i++)
{
int dx = coordX[i] + x;
int dy = coordY[i] + y;
//范围合理
if(dx >= 0 && dx < row && dy >= 0 && dy < col)
{
if(board[dx][dy] == 1)
{
count++;
}
}
}
return count;
}
void gameOfLife(int** board, int boardSize, int* boardColSize)
{
int row = boardSize, col = boardColSize[0];
int** tmpBoard = (int**)malloc(sizeof(int*) * row);
int i,j;
for (i = 0; i < row; i++)
{
tmpBoard[i] = (int*)malloc(sizeof(int) * col);
for (j = 0; j < col; j++)
{
tmpBoard[i][j] = board[i][j];
}
}
for (i = 0; i < row; i++)
{
for (j = 0; j < col; j++)
{
//求出周围或者的细胞有多少个
int live = GetLive(tmpBoard,row,col,i,j);
if(board[i][j] == 1 && (live < 2 || live > 3))
{
board[i][j] = 0;
}
else if(board[i][j] == 0 && live == 3)
{
board[i][j] = 1;
}
}
}
}
5. 分割数组

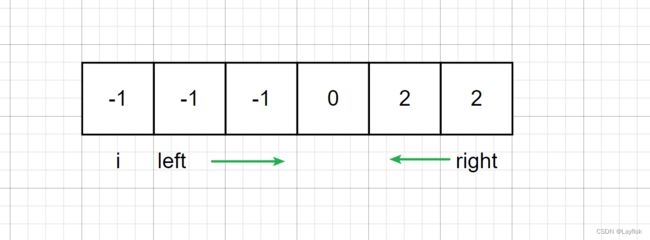
这道题是说将数组分成两部分,左边的数必须全部都小于或者等于右边的数。
- 那么我们可以发现,只要说左边最大的那个数,小于右边最小的那个数就好了。
- 上面这句话都能想到,但是针对于左边和右边这俩区间又该如何选择,这是难点。
- 从右往左,拿一个minRight数组记录着右边出现的最小值,就比如下面这张图,计算出每个区间的最值。
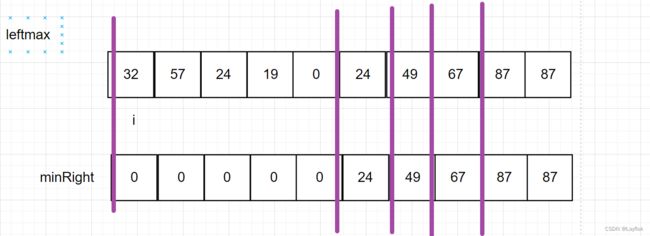
- 有了每个区间的最小值后,再从左边往右遍历,拿一个maxLeft记录当前所走过的最大值,如果发现最大值小于右边的最小值,return 就好了,
- 不能是maxLeft 小于等于 right[i + 1] 因为他要求长度最短,所以 不能等于.
- 还有一种情况就是,如果遍历到numsSize - 1的位置,题目中的测试用例都是合法的。所以只能分成left = [0,numsSize - 1]
下面是代码:
int partitionDisjoint(int* nums, int numsSize)
{
int* minRight = (int*)malloc(sizeof(int) * numsSize);
int i;
minRight[numsSize - 1] = nums[numsSize - 1];
//求出右边数组的最小值
for (i = numsSize - 2; i >= 0; i--)
{
minRight[i] = Min(nums[i],minRight[i + 1]);
}
int maxLeft = nums[0];
for (i = 0; i < numsSize - 1; i++)
{
//左边记录最大的
if(nums[i] > maxLeft)
{
maxLeft = nums[i];
}
if(maxLeft <= minRight[i + 1])
{
//发现左最大数小于了右边最小的数停下来就行了
return i + 1;
}
}
return numsSize - 1;
}
6. 找出数组游戏的赢家

这道题的意思就是就是拿第一个数据和下一个去比较。大的放在第一位,小的去最后一位。
- 第一种情况下:arr[1] < arr[0] 发现可以少去挪动数据的过程直接让i++也是一样的道理
- 同样是指向下一个3.
- 而max还是nums[0]不需要去移动,win++;
- 而如果max 小于了arr[i]时候,更新一下新的max值,和图三意思是一样的。
- 要注意的是,不管之前的win是多少,一定得修改成1,因为这是他第一次赢。
- 中途如果win == k了返回当前的max就好了
- 如果经过这一轮的遍历都没有能达到k次的数。返回最大值就好了。
int Max(int x, int y)
{
return x > y ? x : y;
}
int getWinner(int* arr, int arrSize, int k)
{
int i = 1,max = arr[0],win = 0;
for (i = 1; i < arrSize; i++)
{
if(max > arr[i])
{
win++;
}
else
{
max = arr[i];
win = 1;
}
if(win == k)
{
return max;
}
}
return max;
}
7.除自身以外数组的乘积

这道题的意思是给一个数组,对不ans[i] = 除了nums[i] 之外的全部元素的乘积。
首先使用暴力双for会超时,还不让用除法。
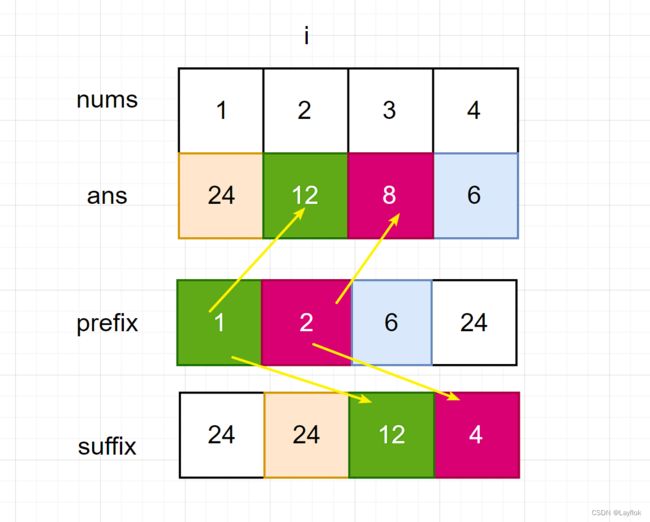
- 看下图,我们可以知道对于nums[i]等于它的前缀积 * 后缀积
- 而首位两项直接采用就好了。
int* productExceptSelf(int* nums, int numsSize, int* returnSize)
{
int* ans = (int*)malloc(sizeof(int) * numsSize);
*returnSize = numsSize;
int* prefix = (int*)malloc(sizeof(int) * numsSize);
int* suffix = (int*)malloc(sizeof(int) * numsSize);
int i,tmp = 1;
//前缀积
for (i = 0; i < numsSize; i++)
{
prefix[i] = (tmp *= nums[i]);
}
//后缀积
tmp = 1;
for (i = numsSize - 1; i >= 0; i--)
{
suffix[i] = (tmp *= nums[i]);
}
//首位两项直接赋值
ans[0] = suffix[1];
ans[numsSize - 1] = prefix[numsSize - 2];
//num[i] = 前缀 * 后缀
for (i = 1; i < numsSize - 1; i++)
{
ans[i] = prefix[i - 1] * suffix[i + 1];
}
return ans;
}
8. 旋转函数

这道题应算肯定是能算,但是一定会超时,需要推导出一个公式来。
- f[0]: 0 nums[0] + 1*nums[1] + 2*nums[2] + 3*nums[3]
- f[1]: 1*nums[0] + 2*nums[1] + 3*nums[2] + 0*nums[3]
- f[2]: 2*nums[0] + 3*nums[1] + 0*nums[2] + 1*nums[3]
- f[1] - f[0] = nums[0] + nums[1] + nums[2] + nums[3] - 4*nums[3]
- f[1] = f[0] + numSum - 4 * nums[4 - 1];
- f[2] - f[1] = nums[0] + nums[1] + nums[2] + nums[3] - 4*nums[2]
- f[2] = f[1] + numSum - 4 * nums[4 - 2];
-所以 f[n] = f[n-1] + numSum - numsSize * nums[numSize - n];
int maxRotateFunction(int* nums, int numsSize)
{
int f = 0, sum = 0;// f为旋转函数的值,sum为数组全部数据之和
int i;
//先求出f[0]的值,即可求出f[1].......f[n-1]的值
for (i = 0; i < numsSize; i++)
{
f += i * nums[i];
sum += nums[i];
}
int ans = f;
for (i = 1; i < numsSize; i++)
{
//公式
f = f + sum - numsSize * nums[numsSize - i];
ans = Max(ans,f);
}
return ans;
}
9. 旋转图像
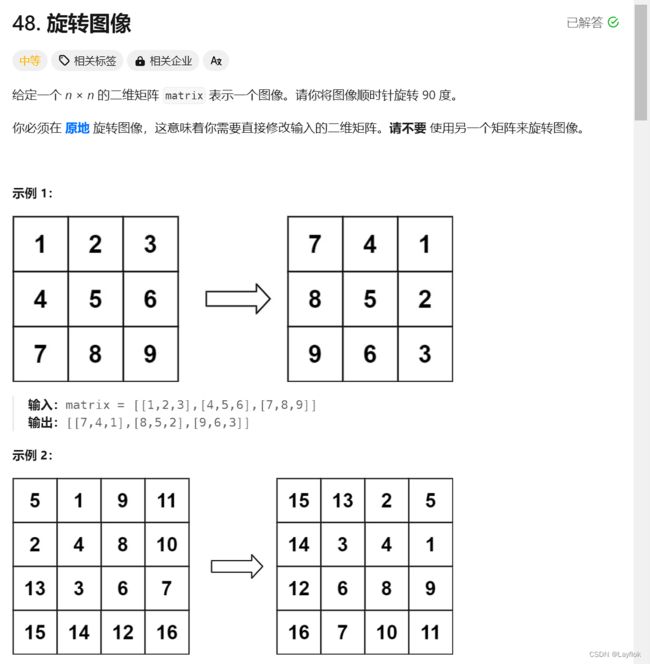
这道题的的意思是,将第一行变成最后一列,第二行变成倒数第二列…
如果创建一个辅助矩阵,直接赋值是可以的,但是题目中的意思是原地修改。
- 我们可以先将矩阵按照副对角线反转矩阵。
- 然后将每一列进行逆序就可以了。
void Swap(int* x, int* y)
{
int tmp = *x;
*x = *y;
*y = tmp;
}
void rotate(int** matrix, int matrixSize, int* matrixColSize)
{
int n = matrixSize;
int i,j;
//先沿着副对角线反转
for (i = 0; i < n - 1; i++)
{
for (j = 0; j < n - i - 1; j++)
{
Swap(&matrix[i][j],&matrix[n - j - 1][n - i - 1]);
}
}
//将矩阵每一列进行逆序。
for (i = 0; i < n; i++)
{
int top = 0, low = n - 1;
while(top < low)
{
Swap(&matrix[top++][i],&matrix[low--][i]);
}
}
}
10.递增三元子序列

这道题是要求我们在数组中找到三个下标i j k 使其呈递增数列,i j k 下标可以不连续,但是必须满足 i < j < k的形式
(1)两次遍历
- 要想递增,那么左边的数也就是 i下标 那个数一定得是最小的。
- 相反右边 k 下标所对应的数一定是大,
- 所以我们可以通过两次遍历,分别对数组求出左边的最小值,和右边的最大值。
- 然后如果有一个下标 j 满足 minLef < nums[j] < maxRight, 就好了
bool increasingTriplet(int* nums, int numsSize)
{
int* minLeft= (int*)malloc(sizeof(int) * numsSize);
int* maxRight = (int*)malloc(sizeof(int) * numsSize);
int i;
//分别求出左边最小值和右边的最大值
minLeft[0] = nums[0];
for (i = 1; i < numsSize; i++)
{
minLeft[i] = Min(minLeft[i-1],nums[i]);
}
maxRight[numsSize - 1] = nums[numsSize - 1];
for (i = numsSize - 2; i >= 0; i--)
{
maxRight[i] = Max(maxRight[i + 1],nums[i]);
}
for (i = 1; i < numsSize - 1; i++)
{
if(nums[i] > minLeft[i-1] && nums[i] < maxRight[i+1])
{
return true;
}
}
return false;
}
(2)贪心
- 需要我们在遍历数组的时候,用两个变量,维护者第一个数和第二个。
- 如果当前的数大于了第二个数,就意味着找了 return true
- 如果当前的数小于第二个数,你就得接着去判断,看看当数和第一个数之间的关系。
- 小于第一个数,那么替换他。
- 否则,就替换第二个数。
bool increasingTriplet(int* nums, int numsSize)
{
int frist = nums[0],second = INT_MAX;
int i;
for (i = 1; i < numsSize; i++)
{
if(nums[i] > second)
{
return true;
}
else if(nums[i] > frist)
{
second = nums[i];
}
else
{
frist = nums[i];
}
}
return false;
}
11. 优美的排列

这道题的是要我输出从1 - n 的数列,将其按照一种规则去排序。
而这种规则就是,这个数列的差值列表里面必须有 k 中不同的数,就是下面这张图。
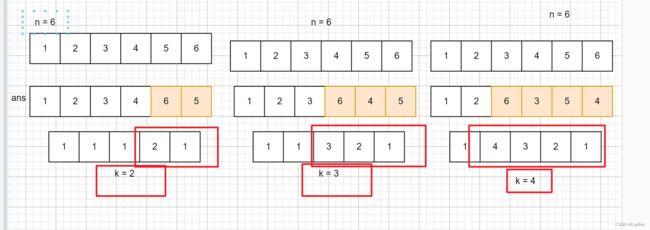
答案数组不是唯一的,上面只是一种。
- 那通过观看上图也能得到一个规律
- 就是我们可以以一种前 (n - k) 个数是升序的,[1,n-k]升序
- 而从n-k之后的数,对其相邻的插入ans中即可。
int* constructArray(int n, int k, int* returnSize)
{
int* ans = (int*)malloc(sizeof(int) * (n+1));
int size = 0;
int i;
for (i = 1; i <= n - k; i++)
{
ans[size++] = i;
}
int left = i, right = n;
while(left < right)
{
ans[size++] = right--;
if(left != right)
{
//如果相同的时候,在外面会统一处理
ans[size++] = left++;
}
}
ans[size++] = left;
*returnSize = size;
return ans;
}
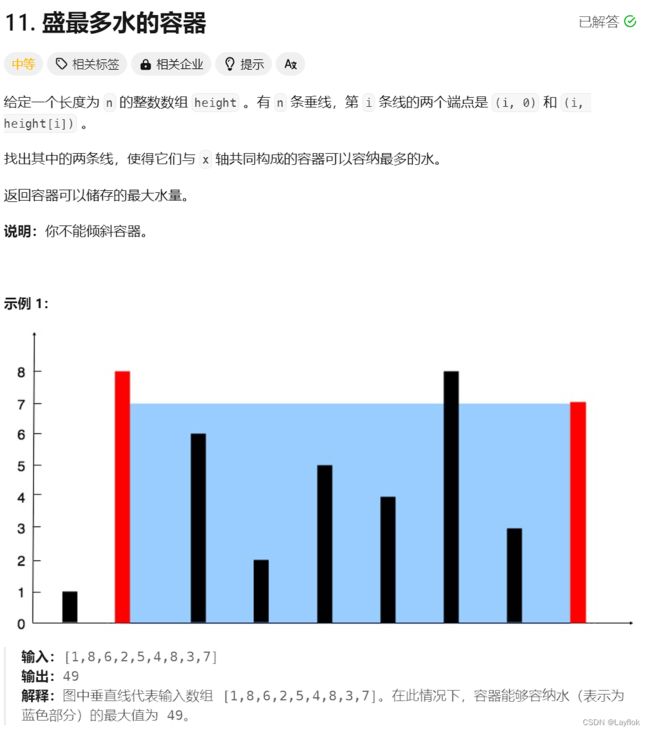
12.盛最多水的容器
- 双指针,哪一边小,哪一边移动。
int maxArea(int* height, int heightSize)
{
int left = 0, right = heightSize - 1;
int ans = 0;
while(left < right)
{
int capacity = Min(height[left],height[right]) * (right - left);
if(height[left] < height[right])
{
left++;
}
else
{
right--;
}
ans = Max(ans,capacity);
}
return ans;
}
13. 三数之和

这道题是要求取数组中不同的下标 i j k 使得其和等于 0 .而且元素不能重复。
- 首先我们得对数组进行排序,这样子才能去重。
- 第一步,确定一个 i 下标,也就是a的位置,这个直接遍历就好了。
- 第二步,确立b 和 c 的位置,因为a + b + c 需要等于 0 。
- 而b和c的位置可以用双指针,来寻找,因为该数组已经是有序的了。
- 如果发现 a + b + c = 0,那么就将其放入到结果中去。
去重
但是最关键的,还得是去重这个步骤,如何去去重,
-
首先看a如何去去重,下图中如果 i 和 i - 1的数相同,就意味着,nums[i - 1] 已经是走过一轮的选手了,没必要继续用它来当a,所以直接进去下一轮循环就好了。
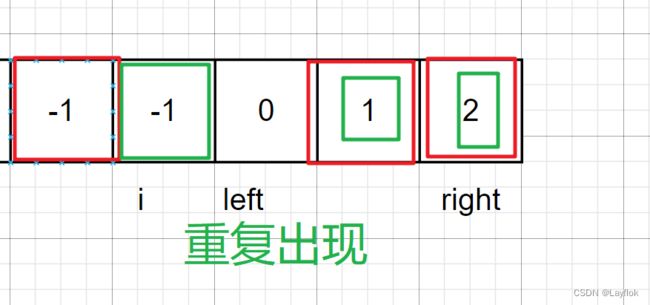
-
而b 和 c 的去重则是在一起,前提是他俩已经是可以满足ans的条件,因为只有满足这个条件你去重才有意义啊。
-
比如下图中如果当前的left或者right 等于了你下一个要去的位置。
int cmp_int(const void* x, const void* y)
{
return *(int*)x - *(int*)y;
}
int** threeSum(int* nums, int numsSize, int* returnSize, int** returnColumnSizes)
{
int** ans = (int**)malloc(sizeof(int*) * 18000);
*returnColumnSizes = (int*)malloc(sizeof(int) * 18000);
qsort(nums,numsSize,sizeof(int),cmp_int);
int i, size = 0;
for (i = 0; i < numsSize - 2; i++)
{
if(nums[i] > 0)
{
//数组依然是有序的,a直接大于了0,后面在怎么加也不会比0小了
break;
}
if(i > 0 && nums[i] == nums[i - 1])
{
//去重,a
continue;
}
int left = i + 1, right = numsSize - 1;
while(left < right)
{
if(nums[i] + nums[left] + nums[right] < 0)
{
left++;
}
else if(nums[i] + nums[left] + nums[right] > 0)
{
right--;
}
else
{
//获取三元组
ans[size] = (int*)malloc(sizeof(int) * 3);
ans[size][0] = nums[i];
ans[size][1] = nums[left];
ans[size][2] = nums[right];
(*returnColumnSizes)[size++] = 3;
//将 b 和 c 去重
while(left < right && nums[left] == nums[left + 1]) left++;
while(left < right && nums[right] == nums[right - 1]) right--;
//同时向中间靠拢
left++;
right--;
}
}
}
*returnSize = size;
return ans;
}
14.下一个排列

找出当前序列的下一个字典序更大序列,如果没有,那么返回升序数组就好,也就是最小的那个。
- 采取从左到右的遍历方式,去找第一个不满足降序的数据 – i
- 找到i之后,再次从左往右遍历,找到第一个大于i的数j。
- 将他俩交换,然后将i以后的位置升序排列就好了。
void Reverse(int* nums, int left, int right)
{
while(left < right)
{
Swap(&nums[left++],&nums[right--]);
}
}
void nextPermutation(int* nums, int numsSize)
{
int i,j;
//第一遍去找不满足降序的数据
for (i = numsSize - 2; i >= 0; i--)
{
if(nums[i] < nums[i + 1])
{
break;
}
}
if(i >= 0)
{
//去[i,n]中去找第一个大于i的数
for (j = numsSize - 1; j > i; j--)
{
if(nums[j] > nums[i])
{
break;
}
}
//交换
Swap(&nums[i],&nums[j]);
}
//重新将(i,numsSize)排列成升序
//qsort(nums + i + 1,numsSize - i - 1,sizeof(int),cmp_int);
//因为是降序的,所以直接交换也行
Reverse(nums,i + 1,numsSize - 1);
}
15. Z 字形变换

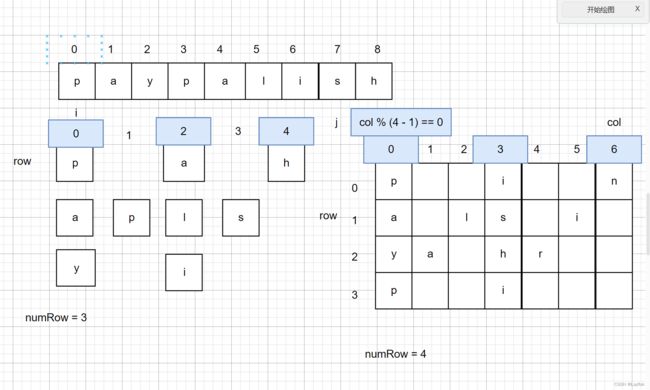
这道题的意思就是将所给的一串字符串对其进行Z字行的摆放,然后再以行序遍历的方式拿出来。
- 首先想到的就是直接模拟,将其放到二维数组中去,进行模拟。
- 模拟也是有条件的,要注意Z自行的变化
有以下三种情况:
- 如果col % (numRow - 1) == 0 的话,就直接让row++,这个是属于竖着一行的
- 如果row == numRow - 1,就说明到头了,需要返回斜着走了,row–,col++;
- 第2点是将其调整成斜方向,注意只是调整,它会会一直斜着走。row–,col++;
将其模拟出来找规律就好了
char* convert(char* s, int numRows)
{
if(numRows == 1)
{
return s;
}
int len = strlen(s);
char* ans = (char*)malloc(sizeof(char) * (len + 1));
char** mat = (char**)malloc(sizeof(char*) * numRows);
int i, pos = 0;
for (i = 0; i < numRows; i++)
{
mat[i] = (char*)calloc((len / 2) + 1,sizeof(char));
}
int row = 0, col = 0;
for (i = 0; i < len; i++)
{
mat[row][col] = s[i];
if (row == numRows - 1)
{
row--;
col++;
}
else if(col % (numRows - 1) == 0)
{
row++;
}
else
{
row--;
col++;
}
}
for (i = 0; i < numRows; i++)
{
for (int j = 0; j <= col; j++)
{
if(mat[i][j] != 0)
{
ans[pos++] = mat[i][j];
}
}
}
ans[pos] = '\0';
return ans;
}
16. 验证IP地址????(可以不看,本人的痛苦回忆)

这道题,我的代码是屎山,我这波是面向测试用例编程的,我有必要记录一下,还有就是下面这样图,为什么能输出这个玩意儿??
思路啥的没有哈,无限的模拟,改bug,。。
单纯的记录一下污点,,,,
char* validIPAddress(char* queryIP)
{
int len = strlen(queryIP);
if(len == 0)
{
return "Neither";
}
int i;
if(len == 4483)
{
return "Neither";
}
if(strchr(queryIP, '.'))
{
int count = 0;
if(queryIP[len - 1] == '.')
{
return "Neither";
}
//Ipv4
for (i = 0; i < len; i++)
{
count++;
int j = i;
int num = atoi(queryIP + i);
if((num != 0 && queryIP[j] == '0') || queryIP[j] == '.' || count > 4 || num > 255)
{
//发现了都一个前导0或者连续两个点。
return "Neither";
}
while(j < len && queryIP[j] != '.')
{
if(isalpha(queryIP[j]))
{
//不能有字母
return "Neither";
}
j++;
}
// int num = atoi(queryIP + i);
// if(num > 255)
// {
// //数字大于了255 也不行
// return "Neither";
// }
if(j - i > 1 && queryIP[i] == '0')
{
return "Neither";
}
//i指向下一个数的第位
i = j;
}
if(count < 4)
{
return "Neither";
}
return "IPv4";
}
else
{
int count = 0;
if(queryIP[len - 1] == ':')
{
return "Neither";
}
//Ipv6
for (i = 0; i < len; i++)
{
count++;
int j = i;
if(queryIP[j] == ':' || count > 8)
{
//说明是0位
return "Neither";
}
while(j < len && queryIP[j] != ':')
{
if(isalpha(queryIP[j]) && !('a' <= tolower(queryIP[j]) && tolower(queryIP[j]) <= 'f'))
{
return "Neither";
}
j++;
}
if(j - i > 4)
{
//16进制小于4
return "Neither";
}
i = j;
}
if(count < 8)
{
return "Neither";
}
return "IPv6";
}
}
17. 破坏回文串

这道题就是说给你一个回文串,你只能改变其中一个字符,然后将其变成不是回文的,并且其字典序还是最小。
- 首先想到的肯定是贪心,如何使字典序最小?
- 将第一个不是a的字符变成a,这个就会是最小的。
- 如果改变之后,是回文的,说明这个串全是a,那么将原字符串最后一个改成b就好了。
bool IsPalindrome(char* s, int len)
{
int left = 0, right = len - 1;
while(left < right)
{
if(s[left++] != s[right--])
{
return false;
}
}
return true;
}
char* breakPalindrome(char* palindrome)
{
int len = strlen(palindrome);
char* ans = (char*)malloc(sizeof(char) * (len + 1));
strcpy(ans,palindrome);
if(len == 1)
{
return "";
}
int i = 0;
while(i < len && palindrome[i] == 'a')
{
i++;
}
//发现第一个不是a的数,将其改成a
if(i < len)
{
ans[i] = 'a';
}
else
{
//说明字符串中全是a,将其最后一个改成b
ans[i - 1] = 'b';
}
//更改后还是回文,说明其中全是a,将它最后一个改成b
if(IsPalindrome(ans,len))
{
palindrome[len - 1] = 'b';
return palindrome;
}
return ans;
}
18. 竖直打印单词
这道题直接暴力枚举就能过的。
- 首先将所给的字符串分割成每个单词
- 然后将每个单词第i位构造成同一个单词,注意有的单词可能没有第 i 位。
- 那么就补充空格
- 最后如果ans中有单词是末尾有空格的话,就把空格去掉就好了。
/**
* Note: The returned array must be malloced, assume caller calls free().
*/
#define MAX_SIZE 10000
//给定一个字符串,将其中的单词转化出来,放入二维数组中去,拿size记录有多少个单词
// 顺带求出里面单词最长的长度
char** GetWord(char* s,int* size,int* wordLen, int* maxLen)
{
int len = strlen(s);
*size = 0;
char** word = (char**)malloc(sizeof(char*) * MAX_SIZE);
int i;
for (i = 0; i < len; i++)
{
char* tmp = (char*)malloc(sizeof(char) * MAX_SIZE);
int pos = 0,j = i;
while(j < len && s[j] != ' ')
{
tmp[pos++] = s[j];
j++;
}
tmp[pos] = '\0';
wordLen[(*size)] = pos;
word[(*size)++] = tmp;
if(*maxLen < pos)
{
*maxLen = pos;
}
i = j;
}
return word;
}
char** printVertically(char * s, int* returnSize)
{
char** ans = (char**)malloc(sizeof(char*) * MAX_SIZE);
int size = 0;
//首先将s分割成每个字符,并且返回每个对应的长度放入wrodLen中去
int wordSize = 0,maxLen = 0;
int* wordLen = (int*)malloc(sizeof(int) * MAX_SIZE);
char** word = GetWord(s,&wordSize,wordLen,&maxLen);
int i;
//构造ans
//i 小于最大的长度
for (i = 0; i < maxLen; i++)
{
char* tmp = (char*)malloc(sizeof(char) * MAX_SIZE);
int pos = 0;
//j 代表每个单词,
for (int j = 0; j < wordSize; j++)
{
//当前单词i位置处无字符填充空格
if(i >= wordLen[j])
{
tmp[pos++] = ' ';
}
else
{
tmp[pos++] = word[j][i];
}
}
tmp[pos] = '\0';
ans[size++] = tmp;
}
//将末尾的空格去掉
for (i = 0; i < size; i++)
{
int j = strlen(ans[i]) - 1;
while(j >= 0 && ans[i][j] == ' ')
{
ans[i][j] = '\0';
j--;
}
}
*returnSize = size;
return ans;
}
19.在LR字符串中交换相邻字符

这道题,只能是拿LX替换XL,XR替换RX,不能说反过来,还有就是它可以倒着往前遍历。。。。

所以还是得找关系。
- 最重要的就是:
- start里面的L位置必须大于等于end里面L的位置。因为变化XL变成LX只会让L的相对对位置变得更小。
- start里面R的位置必须小于等于end俩民R的位置,RX变成XR,R的位置只会越变也大。
bool canTransform(char* start, char* end)
{
int len = strlen(start);
int i = 0, j = 0;
while(i < len && j < len)
{
while(i < len && start[i] == 'X')
{
i++;
}
while(j < len && end[j] == 'X')
{
j++;
}
if(i < len && j < len)
{
if(start[i] != end[j])
{
return false;
}
else
{
//如果是 R 的话, start的R必须在end左边
// start的L必须在end的右边
if((start[i] == 'R' && i > j) || (start[i] == 'L' && i < j))
{
return false;
}
i++;
j++;
}
}
}
while(i < len)
{
if(start[i] != 'X')
{
return false;
}
i++;
}
while(j < len)
{
if(end[j] != 'X')
{
return false;
}
j++;
}
return true;
}
20. 情感丰富的文字

这道题是要我们从给定的word单词数组中,去和所给的s进行比较,满足扩展的要求就算一个,最后返回能有几个满足可以扩张的单词。
- 拿到每一个单词去和字符串s去比较,枚举所有字符
- 如果相对位置的字母不同,肯定不行。
- 如果重复的字符个数不相同的话,就得去判断,重复的是否超过3个了,如果没有超过三个肯定也不行。
- 还有就是如果重复字符的个数都大于了原来的字符个数,也是不行的。
- 最后就是两个字符串不是同时结束,就证明还有未扩张的。
bool Helper(char* s, char* t)
{
int lens = strlen(s), lent = strlen(t);
int i = 0, j = 0;
while(i < lens && j < lent)
{
//相对顺序都不一致,无法扩展
if(s[i] != t[j])
{
return false;
}
int counts = 0,countt = 0;
//去统计重复出现的字符数目
while(i + 1 < lens && s[i] == s[i + 1])
{
i++;
counts++;
}
while(j + 1 < lent && t[j] == t[j + 1])
{
j++;
countt++;
}
//如果不相等,就说明有重复的字符,如果第s小于2就证明不够3个,还有就是如果t重复的比s多了也不行
if((counts != countt) && (counts < 2 || counts < countt))
{
return false;
}
i++;
j++;
}
if(i != lens || j != lent)
{
return false;
}
return true;
}
int expressiveWords(char* s, char** words, int wordsSize)
{
int i, ans = 0;
for (i = 0; i < wordsSize; i++)
{
if (Helper(s,words[i]))
{
ans++;
}
}
return ans;
}
21.字符串转换整数(atoi)
- 首先去空格
- 然后判断第一位是否有效,如果是字母的话,return 0
- 接着判断正负拿flag标记着
- 最后求值,在求值的过程中去判断其是否溢出了,如果溢出之间返回就好了。
int myAtoi(char* s)
{
int len = strlen(s);
int i = 0, flag = 1; //1代表正数,0代表负数
//去空格
while(s[i] == ' ') i++;
//判断是否有效
if(isalpha(s[i]))
return 0;
//判断正负
if(s[i] == '-' || s[i] == '+')
{
if(s[i] == '-')
{
flag = 0;
}
i++;
}
//求出合理的数字长度
int numLen = 0;
int j = i,num = 0;
while(j < len && isdigit(s[j]))
{
numLen++;
j++;
}
//计算
for (j = 0; j < numLen; j++)
{
num += (s[i + j] - '0') * pow(10,numLen - j - 1);
if(num > INT_MAX || num <= INT_MIN)
{
return flag == 1 ? INT_MAX : INT_MIN;
}
}
return flag == 1 ? num : -num;
}
22. HTML实体解析器

这道题是给你一串字符串,然后把里面的特殊符号替换成html解析后的结果,那些结果题目中已经给你了。
- 我们要注意几种特殊情况,如果连续两个&&出现,第一个按照正常的&拷贝就好了。否则的话,我们就要去查找
- 如果说&tmp 包含在题目所给的对应字符中,我们转化,如果没有包含,还是将&tmp拷贝下去就好了。
int Find(char html[6][8],char* tmp)
{
int i = 0;
for (i = 0; i < 6; i++)
{
if(strcmp(html[i],tmp) == 0)
{
return i;
}
}
//
//printf("找不到\n");
return -1;
}
char* entityParser(char* text)
{
char html[6][8] = {""","'","&",">","<","⁄"};
char change[6] = {'"','\'','&','>','<','/'};
int len = strlen(text);
char* ans = (char*)malloc(sizeof(char) * (len + 1));
int i, size = 0;
for (i = 0; i < len; i++)
{
//连续的两个&&,按照&拷贝就行。
if( i < len-1 && text[i] == '&' && text[i + 1] != '&')
{
char* tmp = (char*)malloc(sizeof(char) * 1000);
int pos = 0;
int j = i;
while(j < len - 1 && text[j] != ';' && text[j + 1] != '&')
{
tmp[pos++] = text[j];
j++;
}
//中途遇到&需要做特殊的处理
if(text[j + 1] != '&')
tmp[pos++] = ';';
else
tmp[pos++] = text[j];
tmp[pos++] = '\0';
//进行转化
int index = Find(html,tmp);
if(index != -1)
{
ans[size++] = change[index];
}
else
{
memcpy(ans + size,tmp,sizeof(char) * (j - i + 1));
size += (j - i + 1);
}
i = j;
}
else
{
//
ans[size++] = text[i];
}
}
ans[size] = '\0';
return ans;
}
23.无重复的字串

这道题实在所给的字符串中,找出最长的无重复的公共子串,字符串中的字符可以是数字,字母,和符号包括空格组成,所以我们在开辟哈希表的时候,不能单单只是26了。
这道题暴力双for也能过,代码就不展示了,下面用双指针的解法来。
- 将哈希表的初始值全部赋成-1,因为这个哈希表存放的是下标,而不是出现的次数。
- 拿两个指针start 和 end对字符串进行遍历,如果发现其没出现过,将其出现的下标存放到哈希表中去。
- 如果发现出现过,就证明重复了,start变成出现的下一个位置,但要注意,start必须是 <= map[s[end]] 的,如果不小于等于的话,这个start竟然还能退回去?

int lengthOfLongestSubstring(char* s)
{
int* map = (int*)malloc(sizeof(int) * 127);
for (int i = 0; i < 127; i++)
{
map[i] = -1;
}
int len = strlen(s);
int start = 0, end = 0;
int maxLen = 0;
while(end < len)
{
//出现过的,并且star必须得小于等于当前重复的下标的,这样才能保持前进,而不是后退。
if(map[s[end]] != -1 && start <= map[s[end]])
{
//更新开始位置,注意不能包括自身,因为自身已经重复
start = map[s[end]] + 1;
}
map[s[end]] = end;
maxLen = Max(end - start + 1,maxLen);
end++;
}
return maxLen;
}
24. 最长回文子串
(1)暴力美学(YYDS!!)
这道题暴力倒也能过,但是时间肯定慢。
- 就暴力的去遍历么,拿一个函数来看是否是当前的字符串是否是回文,
- 然后再更新长度
bool IsPalindrome(char* s, int left, int right)
{
while(left < right)
{
if(s[left++] != s[right--])
{
return false;
}
}
return true;
}
char* longestPalindrome(char* s)
{
int len = strlen(s);
char* ans = (char*)malloc(sizeof(char) * (len + 1));
if(len == 1)
{
return s;
}
int maxLen = 0;
int i;
for (i = 0; i < len - 1; i++)
{
for (int j = len - 1; j >= i; j--)
{
if(IsPalindrome(s,i,j))
{
if(j - i + 1 > maxLen)
{
strncpy(ans,s + i,j -i + 1);
maxLen = j - i + 1;
}
}
}
}
ans[maxLen] = '\0';
return ans;
}
(2)动态规划
这个就有说法了,时间上比暴力快了不止一点。
- 首先得知道一个概念,就是说如果一个字符串是回文的,那么它的内部也同样是回文的。
- dp[i][j] — i 到 j 是否是回文串
- 所以我们可以得到一个状态转移方程是 dp[i][j] = dp[i +1][j - 1]
- 而如果长度只有2的情况,只需要判断他俩是否相等即可判断回文。
- 长度是1的情况,就是字符本身,肯定也是回文的。
char* longestPalindrome(char* s)
{
int len = strlen(s);
if(len == 1)
{
return s;
}
char* ans = (char*)malloc(sizeof(char) * (len + 1));
int** dp = (int**)malloc(sizeof(int*) * len);
int maxLen = 0;
int i, j, n; //n代表每次循环的长度
for (i = 0; i < len; i++)
{
dp[i] = (int*)calloc(len, sizeof(int));
}
for (n = 1; n <= len; n++)
{
for (i = 0, j = n - 1; j < len; i++,j++)
{
if(n == 1)
{
//自身全部回文
dp[j][j] = 1;
}
else if(n == 2)
{
//判断ij是否相等,从而决定是否回文
dp[i][j] = s[i] == s[j] ? 1 : 0;
}
else if(s[i] == s[j])
{
//首位相同再去判断其中间是否回文
dp[i][j] = dp[i + 1][j - 1];
}
if(dp[i][j] == 1 && maxLen < j - i + 1)
{
strncpy(ans,s + i, j - i + 1);
maxLen = j - i + 1;
}
}
}
ans[maxLen] = '\0';
return ans;
}
(3)双指针(中心扩散)
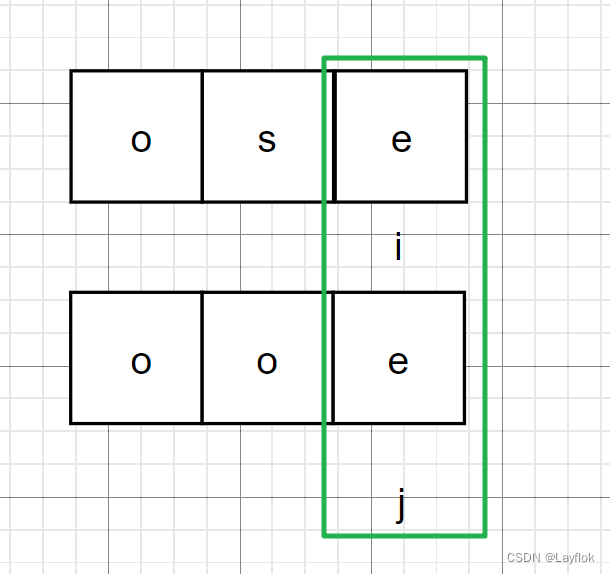
说实话,这个6啊。前两种方式都是从两边往中间走去判断是否回文,这种方式是从中间往外边扩散的去判断,这中方式分偶数串和奇数串两种。
就比如图,一个在b的位置需要对 b - 1 和 b + 1 的位置开始
而偶数字符串则需要对 a 和 a + 1 的位置开始。
所以要对中一个字符串进行两次。

void Helper(char* s,int len, int left, int right, int* start, int* maxLen)
{
//回文判断,中心往外扩
while(left >= 0 && right < len && s[left] == s[right])
{
left--;
right++;
}
//如果新的长度大于了maxlen,更新
if(right - left - 1 > *maxLen)
{
*start = left + 1;
*maxLen = right - left - 1;
}
}
char* longestPalindrome(char* s)
{
int len = strlen(s);
if(len == 1)
{
return s;
}
int i, start = 0, maxLen = 0;
for (i = 0; i < len; i++) //奇数长度
{
Helper(s,len,i - 1, i + 1,&start, &maxLen);
}
for (i = 0; i < len; i++) //偶数长度
{
Helper(s,len, i, i + 1,&start, &maxLen);
}
s[start + maxLen] = '\0';
return s + start;
}
25.整数转罗马数字
- 我么需要一个表来存放数字以及所对应的字符,一共也就13个。
- 然后从大到小的去遍历那个表,优先使用大的。
int values[] = {1000, 900, 500, 400, 100, 90, 50, 40, 10, 9, 5, 4, 1};
char* symbols[] = {"M", "CM", "D", "CD", "C", "XC", "L", "XL", "X", "IX", "V", "IV", "I"};
char* intToRoman(int num)
{
char* ans = (char*)malloc(sizeof(char) * 16);
ans[0] = '\0';
for (int i = 0; i < 13; i++)
{
while(num >= values[i])
{
num -= values[i];
strcat(ans, symbols[i]);
}
if(num == 0)
{
break;
}
}
return ans;
}
26. 电话号码的字母组合

这道题目是说给你一串字符串(只包含数字),然后对每个数字之间进行相应的排列组合。
-
我们需要创建一个path数组,来存放当前的路径是什么,同样还需要一个pathSize来维护我们的数组。
-
还需要创建一个ans数组,当path数组满了的时候,就意味着有一条路径已经好了,将其放入ans中去,同样还需要一个ansSIze来去维护。
-
有了这些东西才可以进行代码的实现。
-
创造路径的代码,其实就是一个回溯的过程,
-
对于每一个字母都对其进行相应的排列组合。
#define MAX_SIZE 1000
char* map[] = {"","","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"};
// 0 1 2 3 4 5 6 7 8 9
char** ans; //答案,最终的所有排列组合
char* path; //每一条路径
int ansSize,pathSize,len; //len是所给字符串的长度
void Helper(char* s, int index)
{
if(index == len)
{
//说明当前path数组中已经是构成了一种了。
char* tmp = (char*)malloc(sizeof(char)* (len + 1));
int i;
for (i = 0; i < pathSize; i++)
{
tmp[i] = path[i];
}
tmp[i] = '\0';
//计入答案
ans[ansSize++] = tmp;
return;
}
else
{
char* word = map[s[index] - '0'];
int n = strlen(word); // n 当前数字所对应的长度
int i;
for (i = 0; i < n; i++)
{
path[pathSize++] = word[i];
Helper(s,index + 1);
pathSize--;
}
}
}
char** letterCombinations(char* digits, int* returnSize)
{
len = strlen(digits);
ans = (char**)malloc(sizeof(char*) * MAX_SIZE);
path = (char*)malloc(sizeof(char) * (len + 1)); //每条路径的长度不就是字符串本身的长度。
ansSize = pathSize = 0;
if(len == 0)
{
*returnSize = 0;
return ans;
}
//开始的下标,
Helper(digits, 0);
*returnSize = ansSize;
return ans;
}
27.外观数列

这道题就是。比如:
第n项:111122233
第n+1项 4个1 + 3个2 + 2个3
所以是413223就好了。
- 所以我们可以由前一项得到后一项,有点动态规划的意思吧。
- 拿如究竟改如何转化,计算出当前重复出现的次数,然后次数放前面,字符放后面。
#define MAX_SIZE 8000
char* Hlper(char* s)
{
int len = strlen(s);
char* ans = (char*)malloc(sizeof(char) * MAX_SIZE);
int size = 0;
int i = 0;
while(i < len)
{
int j = i, count = 0;
while(j < len && s[i] == s[j])
{
count++;
j++;
}
size += sprintf(ans + size,"%d%c",count,s[i]);
i = j;
}
ans[size] = '\0';
return ans;
}
char* countAndSay(int n)
{
char** dp = (char**)malloc(sizeof(char*) * 31);
dp[0] = "1";
for (int i = 1; i <= n; i++)
{
dp[i] = Hlper(dp[i-1]);
}
return dp[n-1];
}
28.编辑距离

这道题是给两个字符串,然后将word1经过一系列操作后,变成word2,只能增,删,替换,求操作最少的次数。
- 动态规划来解决。
- 首先有两个字符串,所以dp[len1][len2]就是说最少的操作次数,dp数组为二维。
- 然后将dp数组进行初始化的值呢,想象一下,如果说len1 = 0 len2 = n.
- 无论如何要变成len1,都得将len2全部删除,或者是将len1t添加到len2的长度。
- 所以对于一个空串dp[0][j] 和 dp[j][0] 他俩都是等于 j 的。
接下来看dp[i][j]的状态转移方程组:
- word[ i ] == word[ j ] 末尾两个字母相同,意味着不用去进行操作去看前一个的操作次数就好了
- dp[ i ][ j ] = dp[ i - 1][ j - 1].
看上图也能发现,难的就是说,如果两者不同,究竟该如何去求。
分一下三种情况(注意 i 和 j 是长度,代表字符串的长度不是下标):
删除 i : dp[i][j] = dp[ i - 1][ j ] + 1。
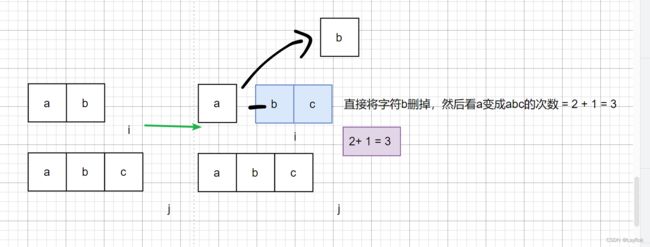
删除 j : dp[ i ][ j ] = dp[ i ][ j - 1] + 1.

替换:dp[i][j] = dp[i - 1][j - 1] + 1;
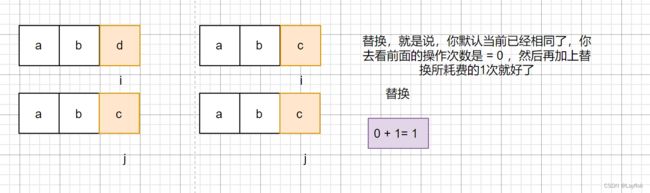
为什么说只有删除和替换,而没有插入,因为对于word1是删除成word2,不也就是word2添加成word1吗?这两者是相对的。
综上所述呢,一共就这三种情况,所以我们选择最小的那个。
代码如下:
int Min(int x, int y)
{
return x < y ? x : y;
}
int minDistance(char* word1, char* word2)
{
int len1 = strlen(word1), len2 = strlen(word2);
int** dp = (int**)malloc(sizeof(int*) * (len1 + 1));
int i,j;
for (i = 0; i <= len1; i++)
{
dp[i] = (int*)calloc(len2 + 1,sizeof(int));
}
//初始化dp数组
//这个初始化相当于:长度为 i 的串,要变成长度为0的串,或者相反,它都必须删除或者添加 i 次。
for (i = 0; i <= len1; i++)
{
dp[i][0] = i;
}
for (i = 0; i <= len2; i++)
{
dp[0][i] = i;
}
//构造dp数组
//此时的 i 于 j 充当的是长度,长度为0在上方已经初始化了,长度从1开始。
for (i = 1; i <= len1; i++)
{
for (j = 1; j <= len2; j++)
{
if(word1[i - 1] == word2[j - 1])
{
//如果尾部字符相同,说明当前不用操作,去看上个需要操作了多少次就好了。
dp[i][j] = dp[i - 1][j - 1];
}
else
{
dp[i][j] = Min(dp[i - 1][j - 1],Min(dp[i][j - 1], dp[i - 1][j])) + 1;
}
}
}
return dp[len1][len2];
}
29.解码方法

给你一个字符串,全是数字构成,将其解码,说白了也就是排列组合出全部的可能数,但是要特别注意0这个数字,没有0的映射。
int numDecodings(char * s)
{
if(s[0] == '0')
{
//无法解码
return 0;
}
int len = strlen(s);
int* dp = (int*)calloc(len + 1,sizeof(len + 1));
dp[0] = 1;
for (int i = 1; i <= len; i++)
{
//
if(s[i - 1] != '0')
{
dp[i] = dp[i - 1];
}
//是合理的数 1 ~ 26
if(i >= 2 && (s[i - 2] == '1' || (s[i - 2] == '2' && s[i - 1] <= '6') ) )
{
dp[i] += dp[i - 2];
}
}
return dp[len];
}
30. 交错字符串
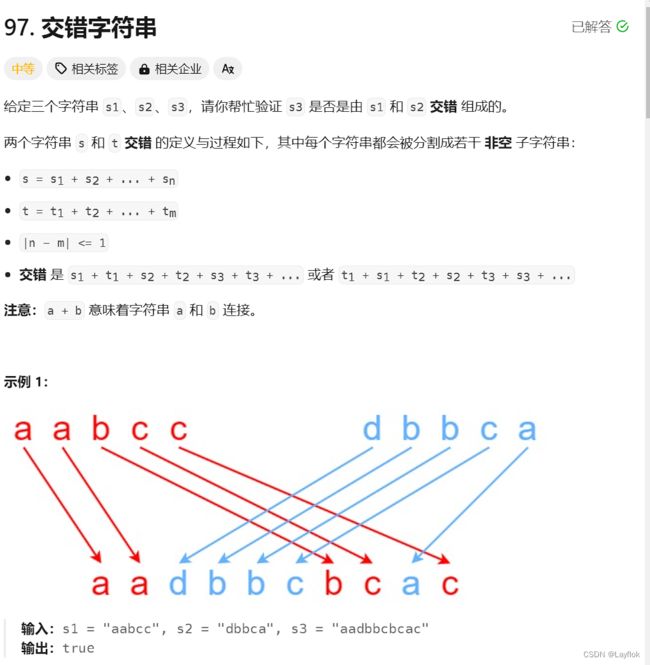
给你三个字符串,判断s3 是否可以由s1和s2交错的构成。
第一反应我真的像题解那样子,确实使用双指针来做的,确实行不通,还是得用动态规划来做。
- 首先我如果要比较是否能构成s3,就说明s3中的字符必须是s1里面的或者是s2里面的。
- 进一步,我们规范一点说,s3每个子字符串的末尾,必须是s1或者s2中的一个。
- 而我们定义一个二维的dp数组.
- dp[i][j] 代表着s1里面i长度的字符串和s2里面j长度的字符串,是否能构成s3里面i + j的字符串。
- 综上第二点,我们可以知道,只要说当前末尾的数据等于了s1,或者s2,我们就去查所对应的前一个是否能交错构成。
if(i > 0 && s1[i -1] == s3 [i + j - 1])
就说明s1的末尾和s3的末尾是一致的,那么就去看s1 i 的前面是否能构成交错。
dp[i][j] = dp[i - 1][j]
if(j > 0 && s2[j - 1] == s3[i + j - 1])
就说明s2的末尾和s3的末尾是一致的,然后去看s2 j之前是否能构成交错。
因为上面的s1先判断,可能经过s1就可以构成交错,s2能不能的无所谓了。
二者满足一个即可
dp[i][j] = dp[i][j] || dp[i][j-1]
bool isInterleave(char* s1, char* s2, char* s3)
{
int lenS1 = strlen(s1), lenS2 = strlen(s2), lenS3 = strlen(s3);
if(lenS1 + lenS2 != lenS3)
{
return false;
}
bool** dp = (bool**)malloc(sizeof(bool*) * (lenS1 + 1));
int i,j;
for (i = 0; i <= lenS1; i++)
{
dp[i] = (bool*)calloc(lenS2 + 1,sizeof(bool));
}
//dp[i][j] 表示从 s1 i 到 s2 j 的长度可以构成 s3 i + j 吗?
//俩空串到空串返回true
dp[0][0] = true;
for (i = 0; i <= lenS1; i++)
{
for (j = 0; j <= lenS2; j++)
{
if(i > 0 && s1[i - 1] == s3[i + j - 1])
{
//末尾相同,那么就去看前面的是否可以构成
dp[i][j] = dp[i - 1][j];
}
if(j > 0 && s2[j - 1] == s3[i + j - 1])
{
dp[i][j] = dp[i][j] || dp[i][j - 1];
}
}
}
return dp[lenS1][lenS2];
}