Java基础
Java 虚拟机的内存划分
为了提高运算效率,就对空间进行了不同区域的划分,因为每一片区域都有特定的处理数据方式和内存管理方式。
方法区
存储已被虚拟机加载的类信息、常量、(静态变量)、即时编译器编译后的代码等数据。
堆内存
存储对象(包括数组对象),new来创建的,都存储在堆内存。
虚拟机栈
用于存储正在执行的每个Java方法的局部变量表等。
局部变量表存放了编译期可知长度的各种基本数据类型、对象引用,方法执行完,自动释放。
程序计数器
程序计数器是CPU中的寄存器,它包含每一个线程下一条要执行的指令的地址。
本地方法栈
当程序中调用了native的本地方法时,本地方法执行期间的内存区域。
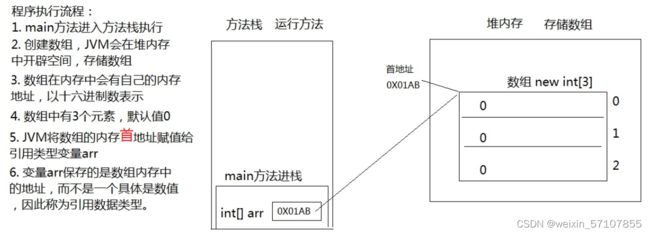
一个一维数组内存图
数组下标为什么是0开始
因为第一个元素距离数组首地址间隔0个单元格。
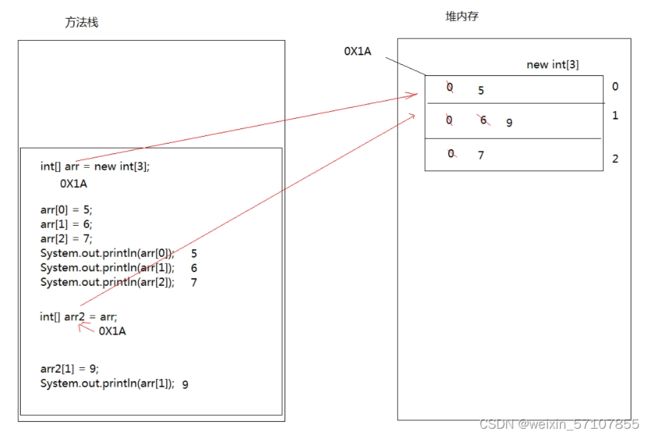
两个一维数组内存图
两个变量指向一个一维数组
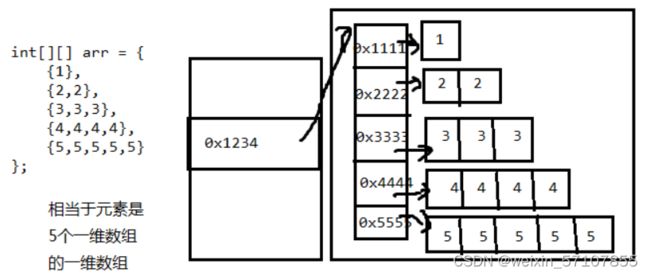
二维数组内存解析
杨辉三角
使用二维数组打印一个 10 行杨辉三角。
提示:
-
第一行有1个元素, 第n行有n个元素
-
每一行的第一个元素和最后一个元素都是1
-
从第三行开始,对于非第一个元素和最后一个元素的元素。即:yanghui[i][j] = yanghui[i-1][j-1] + yanghui[i-1][j];
public class YangHuiTest {
public static void main(String[] args) {
// 10行
int[][] yangHui = new int[10][];
for (int i = 0; i < yangHui.length; i++) {
// 每行初始化
yangHui[i] = new int[i + 1];
// 外层赋值
yangHui[i][0] = yangHui[i][i] = 1;
// 外层数组元素中的非首元素和非末元素赋值
if (i > 1) { // 第二行开始赋值
// 每行赋值
for (int j = 1; j < yangHui[i].length - 1; j++) {
yangHui[i][j] = yangHui[i - 1][j - 1] + yangHui[i - 1][j];
}
}
}
// 遍历输出
for (int i = 0; i < yangHui.length; i++) {
for (int j = 0; j < yangHui[i].length; j++) {
System.out.print(yangHui[i][j] + "\t");
}
System.out.println();
}
}
}求子串最大值
输入一个整形数组,数组里有正数也有负数。数组中连续的一个或多个整数组成一个子数组,每个子数组都有一个和。求所有子数组的和的最大值。要求时间复杂度为O(n)。
public class Test {
public static void main(String[] args) {
int[] arr = new int[]{2, -2, 3, 10, -24, 7, 2, -5};
int i = getGreatestSum(arr);
System.out.println(i);
}
public static int getGreatestSum(int[] arr) {
int greatestSum = 0; //先设置最大值为0
// 数组为空返回默认值0
if (arr == null || arr.length == 0) {
return 0;
}
// 最大值与后一个数相加后进行判断
int temp = greatestSum;
for (int i = 0; i < arr.length; i++) {
// 最大值与下一个数相加
temp += arr[i];
// 如果相加小于0,则相加置0,重新计算最大值
if (temp < 0) {
temp = 0;
}
// 相加后与最大值比较,获取最大值
if (temp > greatestSum) {
greatestSum = temp;
}
}
// 如果数组中都为负数,则返回的默认最大值
if (greatestSum == 0) {
// 设置最大值为第一个负数
greatestSum = arr[0];
for (int i = 1; i < arr.length; i++) {
// 与后一个数比较
if (greatestSum < arr[i]) {
greatestSum = arr[i];
}
}
}
return greatestSum;
}
}创建整数数组(各值不相同)
创建一个长度为6的int型数组,要求数组元素的值都在1-30之间,且是随机赋值。同时,要求元素的值各不相同。
public class Test {
public static void main(String[] args) {
test1();
System.out.println();
test2();
}
public static void test1() {
int[] arr = new int[6];
for (int i = 0; i < arr.length; i++) {
// 赋值 [0,1) [0,30) [1,31)
arr[i] = (int) (Math.random() * 30) + 1;
// 判断下一个数和数组中是否相同
boolean flag = false;
while (true) {
for (int j = 0; j < i; j++) {
// 如果相同,结束判断
if (arr[i] == arr[j]) {
flag = true;
}
break;
}
// 相同则重新赋值
if (flag) {
arr[i] = (int) (Math.random() * 30) + 1;
flag = false;
continue;
}
// 退出判断
break;
}
}
// 遍历输出
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i] + " ");
}
}
public static void test2() {
int[] arr = new int[6];
for (int i = 0; i < arr.length; i++) {
arr[i] = (int) (Math.random() * 30) + 1;
for (int j = 0; j < i; j++) {
if (arr[i] == arr[j]) {
i--;
break;
}
}
}
// 遍历输出
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i] + " ");
}
}
}回形数
public class RectangleTest {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int len = scanner.nextInt();
test1(len);
System.out.println();
test2(len);
}
/*
1 2 3 4
12 13 14 5
11 16 15 6
10 9 8 7
01 02 03 04
12 13 14 05
11 16 15 06
10 09 08 07
*/
/**
* k = 1:向右
* k = 2:向下
* k = 3:向左
* k = 4:向上
*/
public static void test1(int len) {
int[][] arr = new int[len][len];
int s = len * len;
int k = 1; //开始向右赋值
int i = 0, j = 0; // 行 列
for (int m = 1; m <= s; m++) {
if (k == 1) {
// 向右赋值
// 列不超过len 起始值为0
if (j < len && arr[i][j] == 0) {
arr[i][j++] = m;
} else {
k = 2; //向下
i++; //向下 下一行
j--; //回到当前列
m--; //回到当前值
}
} else if (k == 2) {
// 向下赋值
// 行不超过len 起始值为0
if (i < len && arr[i][j] == 0) {
arr[i++][j] = m;
} else {
k = 3; //向左
j--; //向左 上一列
i--; //回到当前行
m--; //回到当前值
}
} else if (k == 3) {
// 向左赋值
if (j >= 0 && arr[i][j] == 0) {
arr[i][j--] = m;
} else {
k = 4; //向上
i--; //向上 上一行
j++; //回到当前列
m--; //回到当前值
}
} else if (k == 4) {
// 向上赋值
if (i >= 0 && arr[i][j] == 0) {
arr[i--][j] = m;
} else {
k = 1; //向左
i++; //向左 上一行
j++; //向下 上一行
m--; //回到当前值
}
}
}
//遍历
for (int m = 0; m < arr.length; m++) {
for (int n = 0; n < arr[m].length; n++) {
System.out.print(arr[m][n] + "\t");
}
System.out.println();
}
}
public static void test2(int len) {
int[][] arr = new int[len][len];
int m = 0; //要显示的数据
int maxX = len - 1; //x轴的最大下标
int maxY = len - 1; //Y轴的最大下标
int minX = 0; //x轴的最小下标
int minY = 0; //Y轴的最小下标
while (minX <= maxX) {
// 向右 x递增赋值
for (int x = minX; x <= maxX; x++) {
arr[minY][x] = ++m;
}
minY++; //向下加1
// 向下 y递增赋值
for (int y = minY; y <= maxY; y++) {
arr[y][maxX] = ++m;
}
maxX--; //向左减1
// 向左
for (int x = maxX; x >= minX; x--) {
arr[maxY][x] = ++m;
}
maxY--; //向上减1
// 向上
for (int y = maxY; y >= minY; y--) {
arr[y][minX] = ++m;
}
minX++; //向右加1
}
for (int i = 0; i < arr.length; i++) {
for (int j = 0; j < arr.length; j++) {
String space = (arr[i][j] + "").length() == 1 ? "0" : "";
System.out.print(space + arr[i][j] + " ");
}
System.out.println();
}
}
}二分查找
public class Test {
public static void main(String[] args) {
int[] arr = new int[]{-99, -54, -2, 0, 2, 33, 43, 256, 999};
int value = 256;
// int value = 25;
test(arr, value);
}
public static void test(int[] arr, int value) {
boolean isFlag = true;
int head = 0;
int end = arr.length - 1;
while (head < end) {
int middle = (head + end) / 2;
if (arr[middle] == value) {
System.out.println("找到指定的元素,索引为:" + middle);
isFlag = false;
break;
} else if (arr[middle] > value) {
end = middle - 1;
} else {
head = middle + 1;
}
}
if (isFlag) {
System.out.println("未找打指定的元素");
}
}
}算法概述
排序
假设含有n个记录的序列为{R1,R2,...,Rn},其相应的关键字序列为{K1,K2,...,Kn}。将这些记录重新排序为{Ri1,Ri2,...,Rin},使得相应的关键字值满足条Ki1<=Ki2<=...<=Kin,这样的一种操作称为排序。
排序的目的是快速查找。
衡量排序算法的优劣
时间复杂度
分析关键字的比较次数和记录的移动次数。
常见的算法时间复杂度由小到大依次为:Ο(1)<Ο(log2n)<Ο(n)<Ο(nlog2n)<Ο(n2)<Ο(n3)<...<Ο(2n)<Ο(n!)
空间复杂度
分析排序算法中需要多少辅助内存
稳定性
若两个记录A和B的关键字值相等,但排序后A、B的先后次序保持不变,则称这种排序算法是稳定的。
排序算法分类
内部排序
整个排序过程不需要借助于外部存储器(如磁盘等),所有排序操作都在内存中完成。
外部排序
参与排序的数据非常多,数据量非常大,计算机无法把整个排序过程放在内存中完成,必须借助于外部存储器(如磁盘)。外部排序最常见的是多路归并排序。可以认为外部排序是由多次内部排序组成。
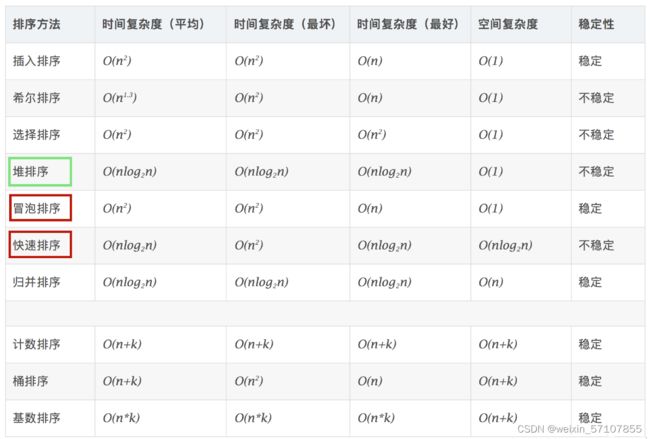
十大内部排序算法
常见时间复杂度所消耗的时间从小到大排序:
O(1) < O(logn) < O(n) < O(nlogn) < O(n^2) < O(n^3) < O(2^n) < O(n!) < O(n^n)
冒泡排序(Bubble Sort)
-
比较相邻的元素。如果第一个比第二个大(升序),就交换他们两个。
-
对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对。这步做完后,最后的元素会是最大的数。
-
针对所有的元素重复以上的步骤,除了最后一个。
-
持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较为止。
public class BubbleSortTest {
public static void main(String[] args) {
int[] arr = {6, 9, 2, 9, 1};
test(arr);
}
public static void test(int[] arr) {
for (int i = 0; i < arr.length - 1; i++) {
boolean flag = true; //假设数组已经是有序的
for (int j = 0; j < arr.length - 1 - i; j++) {
// 希望的是arr[j] < arr[j+1]
if (arr[j] > arr[j + 1]) {
// 交换arr[j]与arr[j+1]
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
flag = false; //如果元素发生了交换,那么说明数组还没有排好序
}
}
if (flag) {
break;
}
}
// 完成排序,遍历结果
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i] + " ");
}
}
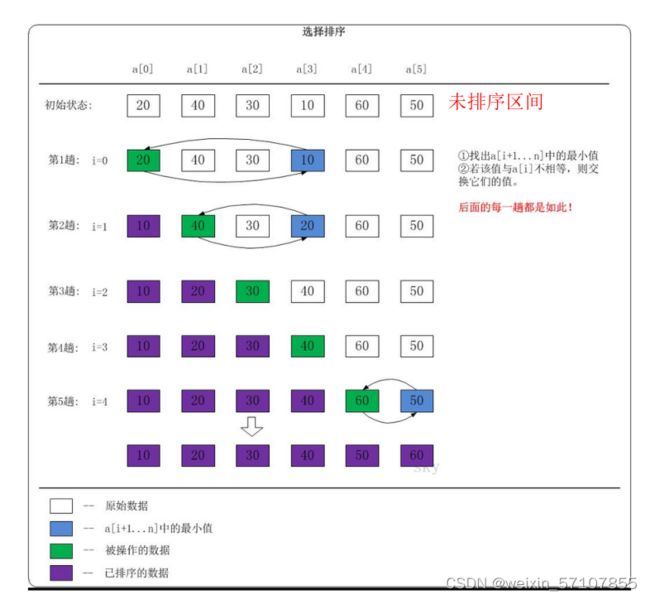
}选择排序
1. 初始状态:无序区间为 Arr[0.1..n],有序区间为空;
2. 第i==1趟排序开始,从无序区中选出最小的元素Arr[k],将它与无序区
的第1个元素交换,从而得到有序区间Arr[0..i-1],无序区间Arr[i..n];
3. 继续后面第i趟排序(i=2,3…n-1),重复上面第二步过程;
4. 第n-1趟排序结束,数组排序完成。
public class SelectionSort {
public static void main(String[] args) {
int[] arr = {5, 2, 6, 5, 9, 0, 3};
System.out.println(Arrays.toString(arr));
selectionSort(arr);
System.out.println(Arrays.toString(arr));
}
public static void selectionSort(int[] arr) {
int len = arr.length;
if (len <= 1) {
return;
}
// 遍历0~len-1进行比较 minIndex
for (int i = 0; i < len - 1; i++) {
int minIndex = i; //记录最小值的位置,默认为i
// minIndex与i+1~len比较 找到最小值下标
for (int j = i + 1; j < len; j++) {
if (arr[minIndex] > arr[j]) {
minIndex = j;
}
}
// 交换当前i与minIndex的位置
if (minIndex != i) {
arr[minIndex] = arr[minIndex] ^ arr[i];
arr[i] = arr[minIndex] ^ arr[i];
arr[minIndex] = arr[minIndex] ^ arr[i];
}
// 执行完一次循环,当前索引 i 处的值为最小值,直到循环结束即可完成排序
}
}
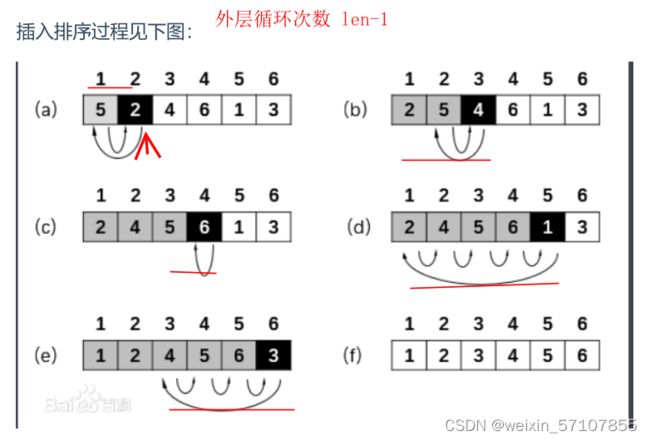
插入排序
1. 将数组分成两部分,已排序、未排序区间,初始情况下,已排序区间
只有一个元素,即数组第一个元素;
2. 取未排序区间中第一个元素,插入到已排序区间中合适的位置,这样
子就得到了一个更大的已排序区间;
3. 重复这个过程,直到未排序区间中元素为空,算法结束。
public class InsertionSort {
public static void main(String[] args) {
int[] arr = {5, 2, 6, 5, 9, 0, 3};
System.out.println(Arrays.toString(arr));
insertionSort(arr);
System.out.println(Arrays.toString(arr));
}
public static void insertionSort(int[] arr) {
int len = arr.length;
if (len <= 1) {
return;
}
// 遍历未排序1~len
for (int i = 1; i < len; i++) {
int value = arr[i]; //未排序值
int j = i - 1; //取已排序最后一个j
// 遍历已排序找到合适位置
for (; j >= 0; j--) {
// value小于已排序则移动
if (value < arr[j]) {
arr[j + 1] = arr[j]; //已排序最后一个向后移
} else {
break;
}
}
// 将需要插入的元素,放到合适位置
arr[j + 1] = value;
}
}
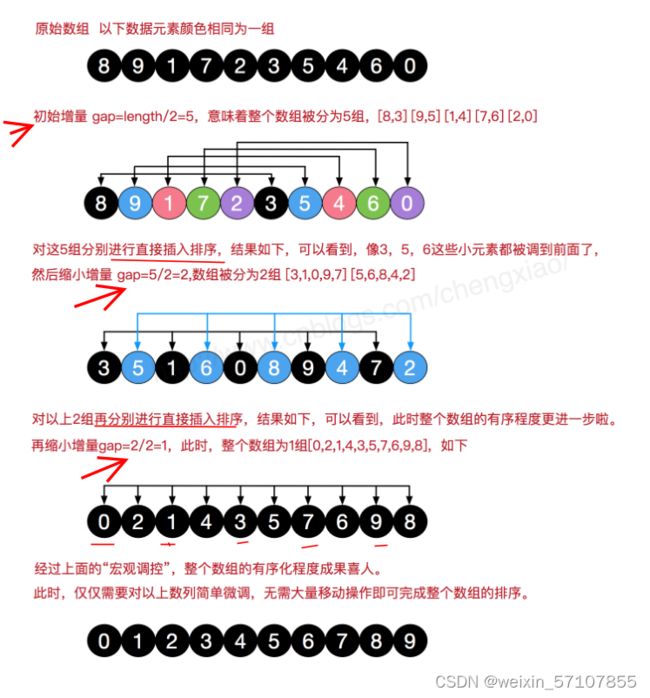
}希尔排序
1. 将有n个元素的数组分成n/2个数字序列,第i个元素和第i+n/2,
i+n/2*m...个元素为一组;
2. 对一组数列进行简单插入排序;
3. 然后,调整增量为n/4,从而得到新的几组数列,再次排序;
4. 不断重复上述过程,直到增量为1,shell排序完全转化成简单插入排
序,完成该趟排序,则数组排序成功。
public class ShellSort {
public static void main(String[] args) {
int[] arr = {5, 2, 6, 5, 9, 0, 3};
System.out.println(Arrays.toString(arr));
shellSort(arr);
System.out.println(Arrays.toString(arr));
}
public static void shellSort(int[] arr) {
int len = arr.length;
if (len <= 1) {
return;
}
// 设置初始增量
int gap = len / 2;
// 由增量控制整体排序次数
while (gap > 0) {
// 遍历gap~len 每组进行排序
for (int i = gap; i < len; i++) {
int value = arr[i]; //记录要插入的值
int j = i - gap; //有序序列的最后一个元素下标
for (; j >= 0; j -= gap) {
// 值小于则后移
if (value < arr[j]) {
arr[j + gap] = arr[j];
} else {
break;
}
}
// 插入值
arr[j + gap] = value;
}
// 缩小增量
gap = gap / 2;
}
}
}归并排序
如果要排序一个数组,先把数组从中间分成前后两部分,然后对前后两部分分别排序,再将排好序的两部分合并在一起,这样整个数组就都有序了
public class MergeSort {
public static void main(String[] args) {
int[] arr = new int[]{5, 2, 6, 9, 0, 3};
System.out.println(Arrays.toString(arr));
int[] newArr = mergeSort(arr);
System.out.println(Arrays.toString(newArr));
}
public static int[] mergeSort(int[] arr) {
// 递归终止条件
if (arr.length < 2) {
return arr;
}
// 拆解数组为两部分
int mid = arr.length / 2;
int[] leftArray = Arrays.copyOfRange(arr, 0, mid);
int[] left = mergeSort(leftArray); //递归
int[] rightArray = Arrays.copyOfRange(arr, mid, arr.length);
int[] right = mergeSort(rightArray);
// 对拆解后两个数组进行合并
return merge(left, right);
}
public static int[] merge(int[] left, int[] right) {
// 定义新数组 len = left.length + right.length
int[] arr = new int[left.length + right.length];
// 往新数组中逐个添加元素
int l = 0, r = 0;
// 遍历
for (int i = 0; i < arr.length; i++) {
if (l >= left.length) {
//左数组已经遍历完成
arr[i] = right[r++];
} else if (r >= right.length) {
//右数组已经遍历完成
arr[i] = left[l++];
} else if (left[l] < right[r]) {
//左数组当前元素值小于右数组
arr[i] = left[l++];
} else {
//右数组当前元素值小于左数组
arr[i] = right[r++];
}
}
return arr;
}
}快速排序(Quick Sort)
-
从数列中挑出一个元素,称为"基准"(pivot),
-
重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任一边)。在这个分区结束之后,该基准就处于数列的中间位置。这个称为分区(partition)操作。
-
递归地(recursive)把小于基准值元素的子数列和大于基准值元素的子数列排序。
-
递归的最底部情形,是数列的大小是零或一,也就是永远都已经被排序好了。虽然一直递归下去,但是这个算法总会结束,因为在每次的迭代(iteration)中,它至少会把一个元素摆到它最后的位置去。
如果要对 first->end 之间的数列进行排序,我们选择 first->end 之间的任意一个元素数据作为分区点(轴值Pivot),然后遍历 first->end 之间所有元素,将小于pivot 的元素放到左边,大于pivot的元素放到右边,pivot放到中间,这样整个数列就被分成了三部分。first->i-1 之间的元素是小于 pivot
的,中间是 pivot,i+1->end 之间的元素是大于 pivot 的。然后再根据分治递归的思想处理两边区间的元素数列,直到区间缩小为 1,整个数列就有序了。
1. 确定轴值,一般取序列中第一位置值
2. 找到序列中轴值所在位置,放置轴值
3. 将小于轴值的所有元素往轴值前面放置,大于轴值的元素往轴值后面放置
public class QuickSort {
public static void main(String[] args) {
int[] arr = {49, 38, 65, 97, 76, 13, 27, 69};
System.out.println(Arrays.toString(arr));
quickSort(arr, 0, arr.length - 1);
System.out.println(Arrays.toString(arr));
}
public static void swap(int[] arr, int i, int j) {
int temp = arr[j];
arr[j] = arr[i];
arr[i] = temp;
}
public static int partition(int[] arr, int i, int j) {
// 默认轴值为 arr[i];
while (i < j) {
// 让j从后往前移动,与轴值arr[i]比较,轴值在前
while (i < j && arr[i] <= arr[j]) {
j--;
}
// arr[i] > arr[j]
if (i < j) {
// 交换i j位置的值
swap(arr, i, j); // 轴值在后
// 更新i的值
i++; //加1
}
// 让i从前往后移动,与轴值arr[j]比较,轴值在后
while (i < j && arr[i] <= arr[j]) {
i++;
}
if (i < j) {
// 再次交换i j位置的值
swap(arr, i, j); // 轴值在前
j--; //减1
}
}
return i;
}
public static void quickSort(int[] arr, int start, int end) {
// 结束条件
if (start >= end) {
return;
}
// 先分段
int index = partition(arr, start, end);
// 对前半截快速排序
quickSort(arr, start, index - 1);
//对后半截快速排序
quickSort(arr, index + 1, end);
}
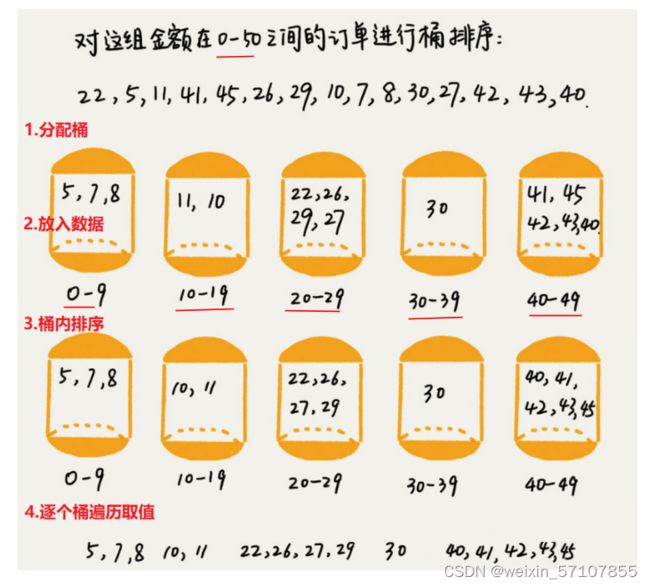
}桶排序
1. 设置固定空桶数
2. 将数据放到对应的空桶中
3. 将每个不为空的桶进行排序
4. 拼接不为空的桶中的数据,得到结果
关键点1:元素值域的划分,即桶中元素的个数,这也决定了桶的数量
关键点2:如何将数组中元素映射到各个桶中
关键点3:如何对各个桶中元素进行排序
注意:待排序数列分布要均匀,避免空桶;同时要兼顾效率和空间,避免空间浪费。
public class BucketSort {
public static void main(String[] args) {
Integer[] array = {5, 2, 2, 6, 9, 0, 3, 4};
List list = Arrays.asList(array);
System.out.println(list);
List bucketSort = bucketSort(list, 3);
System.out.println(bucketSort);
}
public static List bucketSort(List arr, int buketSize) {
//1、递归终止条件 arr为空、arr只有一条数据 桶的容量小于1
if (arr == null || arr.size() < 2 || buketSize < 1) {
return arr;
}
//2、确定桶的个数
//a.找出我们集合中的元素的最大值和最小值
int max = arr.get(0); //最大值
int min = arr.get(0); //最小值
for (int i = 0; i < arr.size(); i++) {
if (max < arr.get(i)) {
max = arr.get(i);
}
if (min > arr.get(i)) {
min = arr.get(i);
}
}
//b.计算桶的个数
int bucketCount = (max - min) / buketSize + 1;
//3、将数据分别放到对应的空桶(list)中
//a.创建所有桶bucketList
List> bucketList = new ArrayList<>();
for (int i = 0; i < bucketCount; i++) {
bucketList.add(new ArrayList());
}
//b.将待排序的数据添加到对应的桶中
for (int i = 0; i < arr.size(); i++) {
//找到该数据应该放置的桶
int bucketIndex = (arr.get(i) - min) / buketSize;
//将该数据放入对应桶中
bucketList.get(bucketIndex).add(arr.get(i));
}
// 桶内元素的排序
List reustList = new ArrayList<>();
//遍历所有桶,逐个进行排序
for (int i = 0; i < bucketList.size(); i++) {
List everyBucket = bucketList.get(i);
if (everyBucket.size() > 0) {
// 桶个数为1,则桶容量减1
if (bucketCount == 1) {
buketSize--;
}
//对子桶进行排序(递归实现 桶排序)
List temp = bucketSort(everyBucket, buketSize);
// 将排好序的
for (int j = 0; j < temp.size(); j++) {
reustList.add(temp.get(j));
}
}
}
return reustList;
}
} 桶排序比较适合用在外部排序中,所谓外部排序,就是说数据存储在外部磁盘中,数据量比较大,而内存有限,无法将数据全部加载到内存中直接进行排序