leetcode 918. Maximum Sum Circular Subarray

Given a circular array C of integers represented by A, find the maximum possible sum of a non-empty subarray of C.

Here, a circular array means the end of the array connects to the beginning of the array. (Formally, C[i] = A[i] when 0 <= i < A.length, and C[i+A.length] = C[i] when i >= 0.)

Also, a subarray may only include each element of the fixed buffer A at most once. (Formally, for a subarray C[i], C[i+1], …, C[j], there does not exist i <= k1, k2 <= j with k1 % A.length = k2 % A.length.)

Example 1:

Input: [1,-2,3,-2]
Output: 3
Explanation: Subarray [3] has maximum sum 3

Example 2:

Input: [5,-3,5]
Output: 10
Explanation: Subarray [5,5] has maximum sum 5 + 5 = 10

Example 3:

Input: [3,-1,2,-1]
Output: 4
Explanation: Subarray [2,-1,3] has maximum sum 2 + (-1) + 3 = 4

Example 4:

Input: [3,-2,2,-3]
Output: 3
Explanation: Subarray [3] and [3,-2,2] both have maximum sum 3

Example 5:

Input: [-2,-3,-1]
Output: -1
Explanation: Subarray [-1] has maximum sum -1

Note:

-30000 <= A[i] <= 30000
1 <= A.length <= 30000

---

给定一个数组，把这个数组看作一个环，则有一个序列为：从选定位置到选定位置的前一位，求这个序列的最大连续子列和。
首先，可以想到的一个很朴素的算法，即枚举数组每一位作为序列的开始，求出最大连续子列和。
但是这样算法复杂度为O(n2),仅在数据量较小的时候可行

---

class Solution {
public:
    int maxSubarraySumCircular(vector& A) {
        if(A.size()==0)
            return 0;
        if(A.size()==1)
            return A[0];
        int len=A.size();
        int sum=0;
        int ans=INT_MIN;
        for(int i=0;i

---

除了这暴力的算法外，还有没有一个更好的设计思路。
在这里，可以分析一下，有如下两种情况：

1. 最大连续子列是数组的子集
   
   在这种情况下，就是照搬求给定序列的最大连续子列和的方法，算出给定数组序列的最大连续子列和

2. 最大连续子列同时包含了数组尾与数组头
   
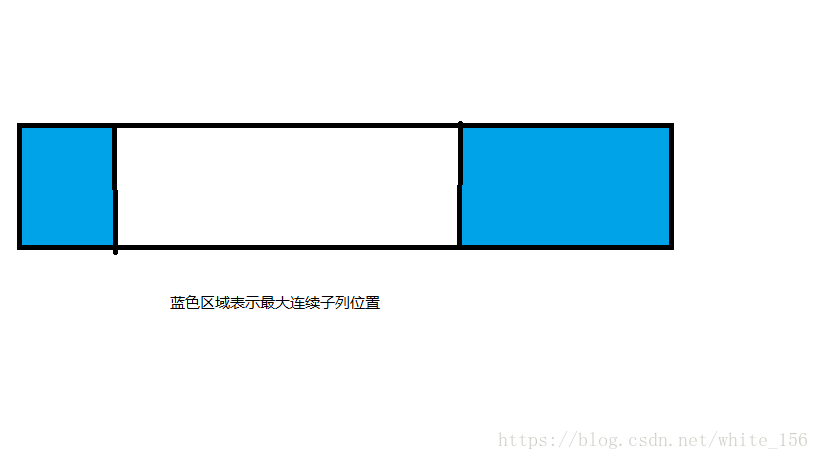
   对于上图，已知蓝色部分为最大连续子列的位置，可以思考一下能否将白色的部分加入到蓝色部分？
   答案很显然是不能的，不难发现，白色的部分有这样的性质：

   从端点到白色区间的任意位置的序列和均为负
   

   根据这一性质，可以得出，白色区间就是数组序列的最小连续子列和。

综上所述，只需要在遍历数组时求出数组的最大连续子列和 与 最下连续子列和进行比较即可

---

class Solution {
public:
    int maxSubarraySumCircular(vector& A) {
        if(A.size()==0)
            return 0;
        if(A.size()==1)
            return A[0];
        int ans=INT_MIN;
        int tol=0;
        int least=0;
        int num=INT_MAX;
        int sum=0;
        for(auto ele : A){
            tol+=ele;
            sum+=ele;
            if(sum<0){
                ans=max(ans,ele);
                sum=0;
            }else{
                ans=max(sum,ans);
            }
            least+=ele;
            if(least>0)
                least=0;
            else
                num=min(least,num);
        }
        if(ans<=0)
            return ans;
        else
            return max(ans,tol-num);
    }
};

---