大数据笔记--Spark（第五篇）

目录

一、Spark的调优

1、更改序列化为kryo

2、配置多临时文件目录

3、启动推测执行机制

4、某些特定场景，用mapPartitions代替map

5、避免使用collect

二、Spark的共享变量

1、广播变量

2、计数器

三、VSM算法

1、什么是倒排索引表？

2、什么是相似度的概念？ 

3、什么是TF-IDF算法

4、VSM算法

Ⅰ、概念

Ⅱ、算法原理

Ⅲ、举例

---

一、Spark的调优

1、更改序列化为kryo

Spark用到序列化的地方：

1）Shuffle时需要将对象写入到外部的临时文件。

2）每个Partition中的数据要发送到worker上，spark先把RDD包装成task对象，将task通过网络发给worker。

3）RDD如果支持内存+硬盘，只要往硬盘中写数据也会涉及序列化。

默认使用的是java的序列化。但java的序列化有两个问题，一个是性能相对比较低，另外它序列化完二进制的内容长度也比较大，造成网络传输时间拉长。业界现在有很多更好的实现，如kryo，比java的序列化快10倍以上。而且生成内容长度也短。时间快，空间小，自然选择它了。

方法一：修改spark-defaults.conf配置文件

设置：

spark.serializer org.apache.spark.serializer.KroySerializer

注意用空格隔开

方法二：启动spark-shell或者spark-submit时配置

--conf spark.serializer=org.apache.spark.serializer.KryoSerializer

方法三：在代码中

val conf = new SparkConf()

conf.set(“spark.serializer”,“org.apache.spark.serializer.KryoSerializer”)

三种方式实现效果相同，优先级越来越高。

通过代码使用kryo：

文件数据：

rose 23

tom 25

person类代码：

class Person(var1:String,var2:Int)  extends Serializable{
  var name=var1
  var age=var2
}

MyKryoRegister类代码：

import org.apache.spark.serializer.KryoRegistrator
import com.esotericsoftware.kryo.Kryo

/**
 * 自定义kryo注册器类，可以将指定的class的序列化由java序列化变为kryo
 */
class MyKryoRegister extends KryoRegistrator {
  def registerClasses(kryo: Kryo): Unit = {
    //注册指定类的序列化kryo
    kryo.register(classOf[Person])
  }
}

KryoDriver代码：

import org.apache.spark.SparkConf
import org.apache.spark.SparkContext
import org.apache.spark.storage.StorageLevel
 
object KryoDriver {
  
  def main(args: Array[String]): Unit = {
    val conf = new SparkConf().setMaster("local").setAppName("kryoTest")
      .set("spark.serializer", "org.apache.spark.serializer.KryoSerializer")
      .set("spark.kryo.registrator", "cn.tedu.MyKryoRegister")
    val sc = new SparkContext(conf)
    
    val data=sc.textFile("d://people.txt")
    
    val userData=data.map { x => new Person(x.split(" ")(0),x.split(" ")(1).toInt) }
    
    userData.persist(StorageLevel.MEMORY_AND_DISK)
    
    userData.foreach(x=>println(x.name))
  }
}

2、配置多临时文件目录

需要挂载到不同的磁盘上

spark.local.dir参数。当shuffle、归并排序（sort、merge）时都会产生临时文件。这些临时文件都在这个指定的目录下。那这个文件夹有很多临时文件，如果都发生读写操作，有的线程在读这个文件，有的线程在往这个文件里写，磁盘I/O性能就非常低。

怎么解决呢？可以创建多个文件夹，每个文件夹都对应一个真实的硬盘。假如原来是3个程序同时读写一个硬盘，效率肯定低，现在让三个程序分别读取3个磁盘，这样冲突减少，效率就提高了。这样就有效提高外部文件读和写的效率。怎么配置呢？只需要在这个配置时配置多个路径就可以。中间用逗号分隔。

spark.local.dir=/home/tmp,/home/tmp2

3、启动推测执行机制

可以设置spark.speculation  true

开启后，spark会检测执行较慢的Task，并复制这个Task在其他节点运行，最后哪个节点先运行完，就用其结果，然后将慢Task 杀死

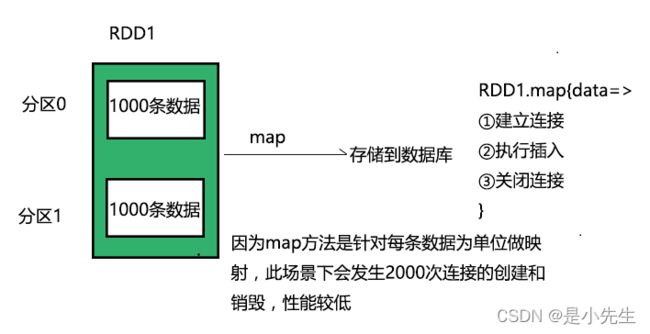
4、某些特定场景，用mapPartitions代替map

map方法对RDD的每一条记录逐一操作。mapPartitions是对RDD里的每个分区操作

rdd.map{ x=>conn=getDBConn.conn;write(x.toString);conn close;}

这样频繁的链接、断开数据库，效率差。

rdd.mapPartitions{(record:=>conn.getDBConn;for(item<-recorders；write(item.toString);conn close;}

这样就一次链接一次断开，中间批量操作，效率提升。

5、避免使用collect

collect只适合在测试时，因为把结果都收集到Driver服务器上，数据要跨网络传输，同时要求Driver服务器内存大，所以收集过程慢。解决办法就是直接输出到分布式文件系统中。

二、Spark的共享变量

Spark程序的大部分操作都是RDD操作，通过传入函数给RDD操作函数来计算。这些函数在不同的节点上并发执行，但每个内部的变量有不同的作用域，不能相互访问，所以有时会不太方便，Spark提供了两类共享变量供编程使用——广播变量和计数器。

1、广播变量

这是一个只读对象，在所有节点上都有一份缓存，创建方法是SparkContext.broadcast()，比如：

scala> val broadcastVar = sc.broadcast(Array(1, 2, 3))
broadcastVar: org.apache.spark.broadcast.Broadcast[Array[Int]] = Broadcast(0)
scala> broadcastVar.value
res0: Array[Int] = Array(1, 2, 3)

注意，广播变量是只读的，所以创建之后再更新它的值是没有意义的，一般用val修饰符来定义广播变量。

2、计数器

计数器只能增加，是共享变量，用于计数或求和。

创建计数器：val accum=SparkContext.accumulator(v, name)，其中v是初始值，name是名称。

操作:accum+=1

获取值：accum.value

scala> val accum = sc.accumulator(0, "My Accumulator")
accum: org.apache.spark.Accumulator[Int] = 0
scala> sc.parallelize(Array(1, 2, 3, 4)).foreach(x => accum += x)
scala> accum.value
res1: Int = 10

三、VSM算法

Vector Space Model向量空间模型算法，此算法可以用于文档排名。

学习这个算法需要对下面三个基础有所了解：

①、倒排索引表

②、相似度的概念

③、TF-IDF算法

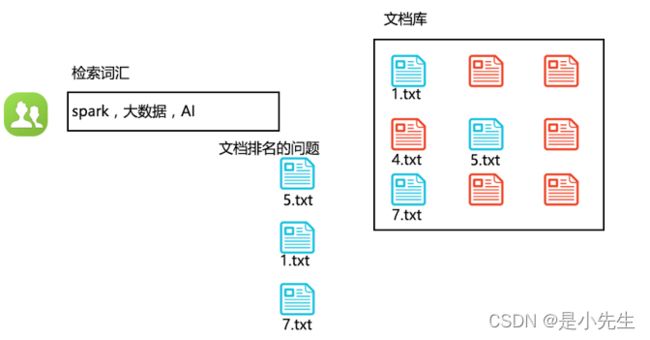
算法解决了什么问题？下图简单的解释，我们检索文档库哪些文档包含我们检索的词汇，找出来之后返回排名怎么办呢？

1、什么是倒排索引表？

正向索引：文档->词汇的索引，比如：

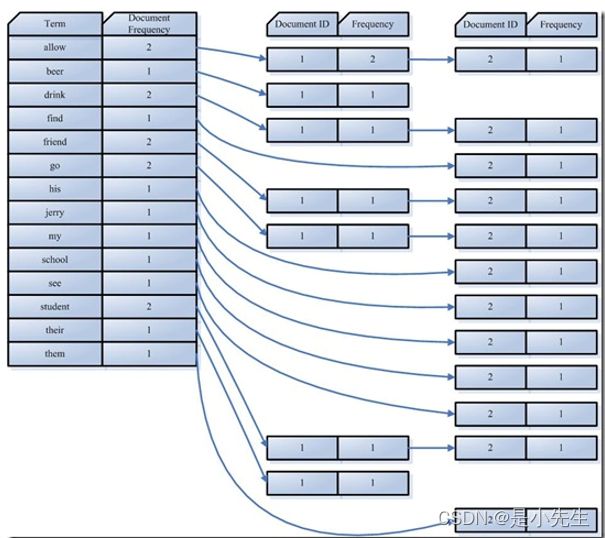
 反向索引（倒排索引）：词汇->文档的索引，比如：

 

2、什么是相似度的概念？ 

上图表示08班与09班的学生毕业后的薪资以及平均薪资。

但是我们如何看出哪个班级就业薪资更稳定呢？这时候一般就会用方差来比较

方差可以用于描述一组数据的散布程度，方差越大，数据月散布，即每个样本离均值越远，方差越小，数据就越集中

        ​​

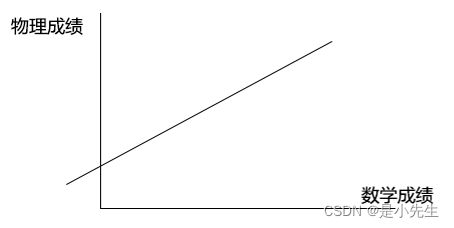
 要研究学生的数学成绩和物理成绩之间的相关性。用均值和方差都无法描述，所以引入：协方差，可以描述变量之间的相关性

我们可以通过协方差的结果来判断变量之间的关系（相关性）

1、如果协方差的值>0，则表示变量之间是正相关（数学好，物理好；数学差，物理差）

 

2、如果协方差=0，则表示变量之间没有任何的相关性

 3、如果协方差的值<0，则表示变量之间负相关（数学好，物理差；数学差，物理好）

现在要进一步研究相关性的强弱，但是协方差的值描述不了。因为协方差会受到变量的量纲影响。所以要描述相关性的强弱，必须要消除变量的量纲影响。消除变量量纲的方法：除以这组变量数据的标准差

所以引入：相关系数，可以描述相关性的强弱

 相关系数的取值范围 0<=|r|<=1

①、r=1，完全正相关，当变量之间存在某种精确的函数关系时，是完全正相关

②、0

③、r=0，完全不相关（极少出现=0的情况）

④、-1

⑤、r=-1，完全负相关

综上，可以根据相关系数的值的大小，判断相关性的强弱（相似度的强弱）

几何角度理解相关系数：向量之间夹角余弦

可描述变量之间相关性（相似度）的强弱

根据公式计算出两个向量的夹角的余弦值：

scala的zip 拉链方法；scala的Math.sqrt()

object Driver {
  def main(args: Array[String]): Unit = {
    val a1 = Array(1,5,3)
    val a2 = Array(3,10,7)
    // 拉链方法
    val a1a2=a1 zip a2
    val a1a2Fenzi=a1a2.map{x=>x._1*x._2}.sum
    val a1Fenmu=Math.sqrt(a1.map{x=>x*x}.sum)
    val a2Fenmu=Math.sqrt(a2.map{x=>x*x}.sum)
    val a1a2Cos=a1a2Fenzi/(a1Fenmu*a2Fenmu)
    println(a1a2Cos)
  }
}

3、什么是TF-IDF算法

是一种用于信息检索与数据挖掘的常用加权技术。TF意思是词频(Term Frequency)，IDF意思是逆文本频率指数(Inverse Document Frequency)。

用以评估一字词对于一个文件集或一个语料库中的其中一份文件的重要程度。字词的重要性随着它在文件中出现的次数成正比增加，但同时会随着它在语料库中出现的频率成反比下降。TF-IDF加权的各种形式常被搜索引擎应用，作为文件与用户查询之间相关程度的度量或评级。

Term Frequency (tf)：即此Term在此文档中出现了多少次。tf 越大说明越重要。

Inverse Document Frequency (idf)：逆向文件频率，即有多少文档包含次Term。df 越大说明越不重要。

算法定义：

整体可以表示：

其中：

 

tf表示词汇在本篇文档出现次数

idf分子D表示一共有多少篇文档

idf分母表示有多少篇文档出现这个词汇

4、VSM算法

Ⅰ、概念

向量空间模型（VSM：Vector Space Model）由Salton等人于20世纪70年代提出，并成功地应用于文本检索系统。

VSM概念简单，把对文本内容的处理简化为向量空间中的向量运算，并且它以空间上的相似度表达语义的相似度，直观易懂。当文档被表示为文档空间的向量，就可以通过计算向量之间的相似性来度量文档间的相似性。文本处理中最常用的相似性度量方式是余弦距离。

向量空间模型 （或词组向量模型) 是一个应用于信息过滤，信息撷取，索引以及评估相关性的代数模型。

Ⅱ、算法原理

①、计算权重的过程

影响一个词在一篇文档种的重要性主要有两个因素：

Term Frequency (tf)：即此Term在此文档中出现了多少次。tf 越大说明越重要。

Document Frequency (df)：即有多少文档包含次Term。df 越大说明越不重要。

模型公式：

：t在文档d中的权重

：t在文档d中出现的频率

n：文件总数

：包含术语t的文档数量

②、判断Term之间的关系从而得到文档相关性的过程，也即向量空间模型的算法(VSM)。

我们把文档看作一系列词(Term)，每一个词(Term)都有一个权重(Term weight)，不同的词(Term)根据自己在文档中的权重来影响文档相关性的打分计算。

于是我们把所有此文档中词(term)的权重(term weight) 看作一个向量。

Document = {term1, term2, …… ,term N}

Document Vector = {weight1, weight2, …… ,weight N}

同样我们把查询语句看作一个简单的文档，也用向量来表示。

Query = {term1, term 2, …… , term N}

Query Vector = {weight1, weight2, …… , weight N}

我们把所有搜索出的文档向量及查询向量放到一个N维空间中，每个词(term)是一维。

我们认为两个向量之间的夹角越小，相关性越大。 所以我们计算夹角的余弦值作为相关性的打分，夹角越小，余弦值越大，打分越高，相关性越大。

Ⅲ、举例

查询语句有11个Term，共有三篇文档搜索出来。其中各自的权重(Term weight)，如下表格

	t1	t2	t3	t4	t5	t6	t7	t8	t9	t10	t11
D1	0	0	.477	0	.477	.176	0	0	0	.176	0
D2	0	.176	0	.477	0	0	0	0	.954	0	.176
D3	0	.176	0	0	0	.176	0	0	0	.176	.176
Q	0	0	0	0	0	.176	0	0	.477	0	.176

 Q表示查询条件，我们计算，三篇文档查询语句相同的相关性打分分别为：

分子如何得到的呢？简单理解为D1的t1与Q的t1相乘加上t2一次相加。0x0+0x0+0.477x0+.... 

分母的值呢？D1的值平方开根号，然后乘以Q的值平方开根号。

 

 

于是文档二相关性最高，先返回，其次是文档一，最后是文档三；到此为止，我们可以找到我们最想要的文档了。