算法竞赛——强连通分量

强连通分量

强连通的定义是：有向图 G 强连通是指，G 中任意两个结点连通。

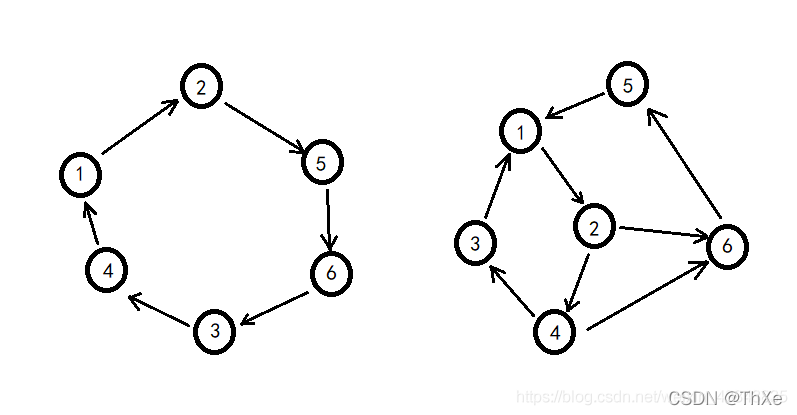
强连通分量（Strongly Connected Components，SCC）的定义是：极大的强连通子图也可以说，在强连图图的基础上加入一些点和路径，使得当前的图不在强连通，称原来的强连通的部分为强连通分量。

DFS生成树

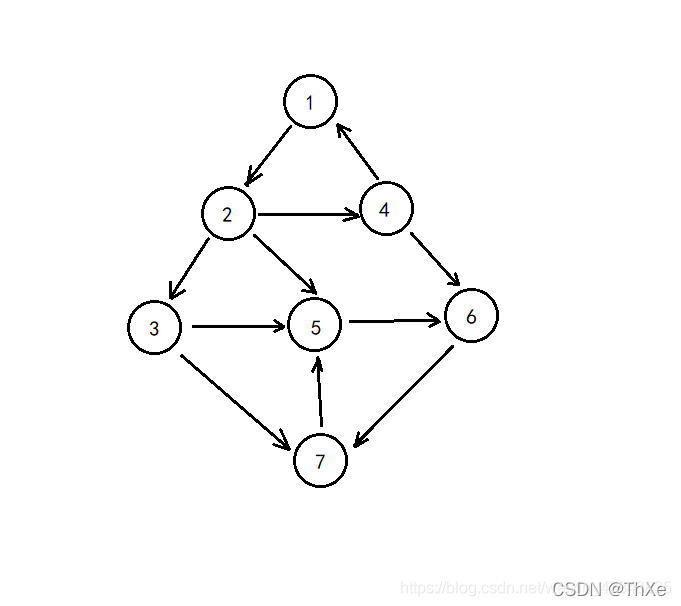
DFS生成树是根据DFS搜索顺序构成的一颗生成树，形如（自上而下，自左而右）：

有向图的 DFS 生成树主要有 4 种边：
树边（tree edge）：示意图中以黑色边表示，每次搜索找到一个还没有访问过的结点的时候就形成了一条树边。
反祖边、反向边（back edge）：示意图中以红色边表示（即7->1 ），也被叫做回边，即指向祖先结点的边。
横叉边（cross edge）：示意图中以蓝色边表示（即 9->7 ），它主要是在搜索的时候遇到了一个已经访问过的结点，但是这个结点 并不是 当前结点的祖先。
前向边（forward edge）：示意图中以绿色边表示（即 3->6 ），它是在搜索的时候遇到子树中的结点的时候形成的。可以看出树边其实是一个特殊的前向边。

两者联系

考虑 DFS 生成树与强连通分量之间的关系。

如果结点 u 是某个强连通分量在搜索树中遇到的第一个结点，那么这个强连通分量的其余结点肯定是在搜索树中以 u为根的子树中。结点 u被称为这个强连通分量的根。

反证法：假设有个结点 v在该强连通分量中但是不在以 u为根的子树中，那么 u到 v的路径中肯定有一条离开子树的边。但是这样的边只可能是横叉边或者反祖边，然而这两条边都要求指向的结点已经被访问过了，这就和 u 是第一个访问的结点矛盾了，命题得证。

Tarjan 算法求强连通分量

在 Tarjan 算法中为每个结点 u维护了以下几个变量：

$df{n}_u$：深度优先搜索遍历时结点 u被搜索的次序。
$lo{w}_u$：能够回溯到的最早的已经在栈中的结点。设以 u为根的子树为$Subtre{e}_u$。$lo{w}_u$ 定义为以下结点的 dfn的最小值：$Subtre{e}_u$中的结点；从$Subtre{e}_u$ 通过一条不在搜索树上的边能到达的结点。
一个结点的子树内结点的 dfn 都大于该结点的 dfn。

从根开始的一条路径上的 dfn 严格递增，low 严格非降。

按照深度优先搜索算法搜索的次序对图中所有的结点进行搜索。在搜索过程中，对于结点 u和与其相邻的结点 v(v 不是u 的父节点）考虑 3 种情况：
v 未被访问：继续对 v进行深度搜索。在回溯过程中，用 $lo{w}_v$更新$lo{w}_u$ 。因为存在从 u 到v 的直接路径，所以 v能够回溯到的已经在栈中的结点，u也一定能够回溯到。
v 被访问过，已经在栈中：根据 low 值的定义，用 $df{n}_v$更新 。
v被访问过，已不在栈中：说明 v已搜索完毕，其所在连通分量已被处理，所以不用对其做操作。
对于一个连通分量图在该连通图中有且仅有一个 u使得$df{n}_u==lo{w}_u$ 。该结点一定是在深度遍历的过程中，该连通分量中第一个被访问过的结点，因为它的 dfn 和 low 值最小，不会被该连通分量中的其他结点所影响。

因此，在回溯的过程中，判定$df{b}_u==lo{w}_u$ 是否成立，如果成立，则栈中 u及其上方的结点构成一个 SCC。

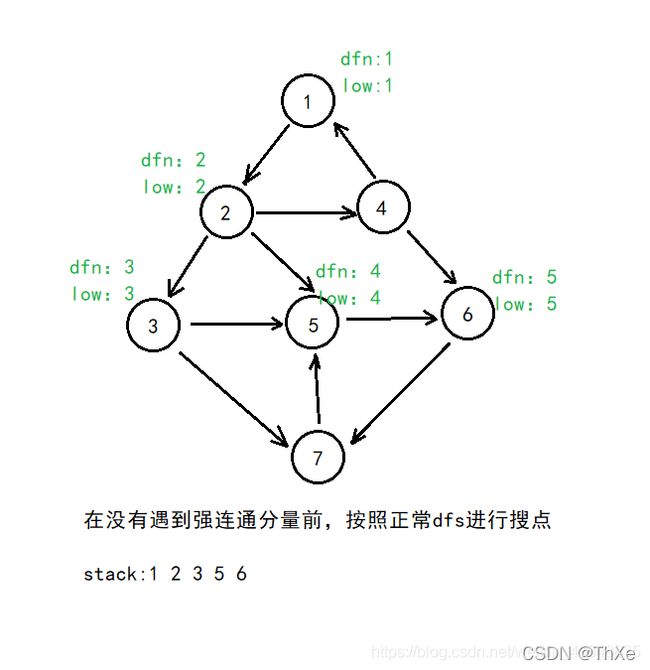
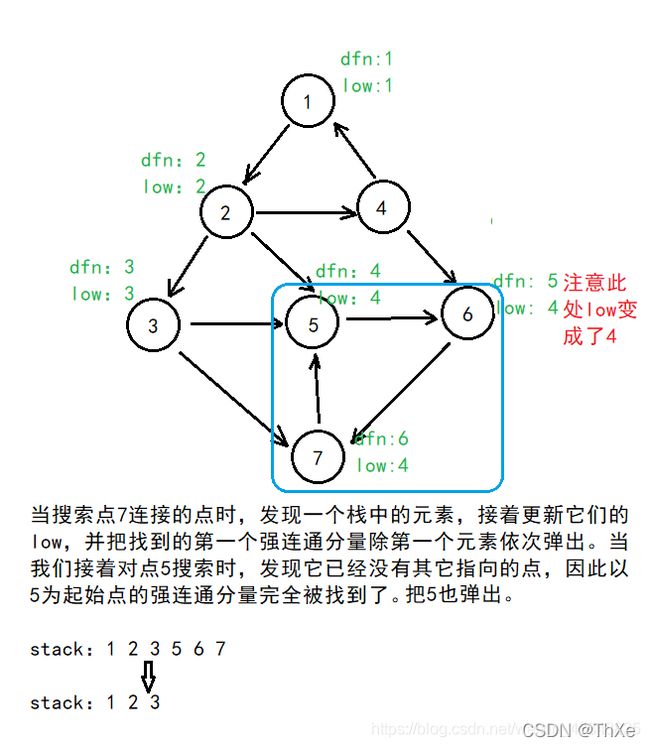
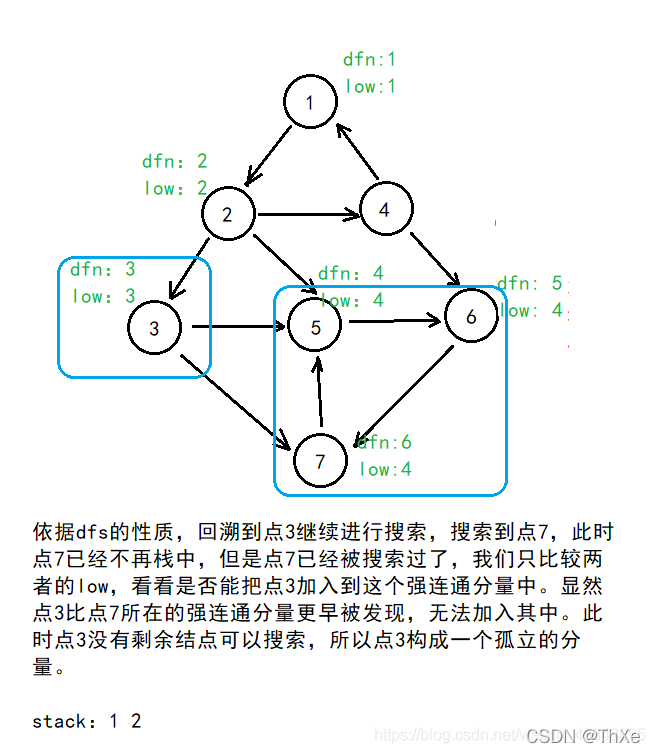
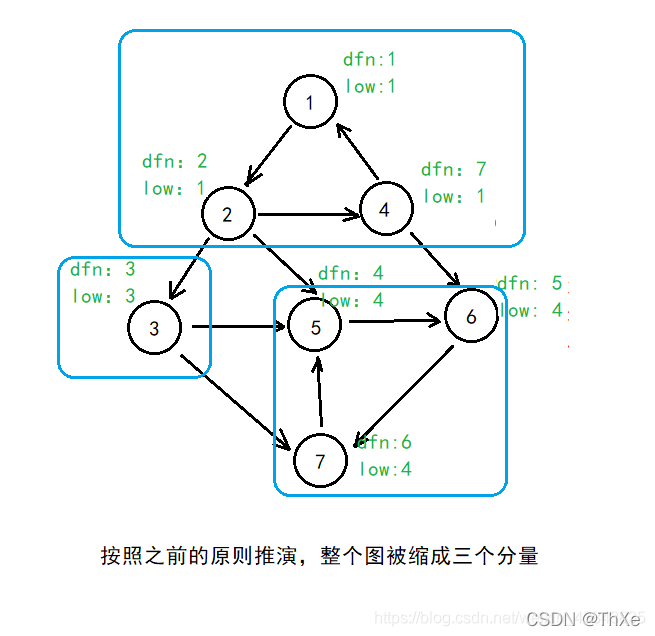
Tarjan算法图示

Tarjan 伪代码与模板

伪代码：

TARJAN_SEARCH(int u)
    vis[u]=true
    low[u]=dfn[u]=++dfncnt
    push u to the stack
    for each (u,v) then do
        if v hasn't been searched then
            TARJAN_SEARCH(v) // 搜索
            low[u]=min(low[u],low[v]) // 回溯
        else if v has been in the stack then
            low[u]=min(low[u],dfn[v])

模板：

// C++ Version
int dfn[N], low[N], dfncnt, s[N], in_stack[N], tp;
int scc[N], sc;  // 结点 i 所在 SCC 的编号
int sz[N];       // 强连通 i 的大小

void tarjan(int u) {
  low[u] = dfn[u] = ++dfncnt, s[++tp] = u, in_stack[u] = 1;
  for (int i = h[u]; i; i = e[i].nex) {
    const int &v = e[i].t;
    //未访问，递归遍历
    if (!dfn[v]) {
      tarjan(v);
      low[u] = min(low[u], low[v]);
    } //访问过，且在栈中
    else if (in_stack[v]) {
      low[u] = min(low[u], dfn[v]);
    }
  }
 if(dfn[u]==low[u])
    {
        int y;
        ++scc_cnt;//强连通分量总数+1
        do
        {
            y = stk[top--];//取栈顶元素y
            in_stk[y] = false;//则y不再在栈中
            id[y] = scc_cnt;
            Size[scc_cnt] ++;//第scc_cnt个连通块点数+1
        }while(y!=u);
}

相关题目

受欢迎的牛
每一头牛的愿望就是变成一头最受欢迎的牛。

现在有 N 头牛，编号从 1 到 N，给你 M 对整数 (A,B)，表示牛 A 认为牛 B 受欢迎。

这种关系是具有传递性的，如果 A 认为 B 受欢迎，B 认为 C 受欢迎，那么牛 A 也认为牛 C 受欢迎。

你的任务是求出有多少头牛被除自己之外的所有牛认为是受欢迎的。

输入格式
第一行两个数 N,M；

接下来 M 行，每行两个数 A,B，意思是 A 认为 B 是受欢迎的（给出的信息有可能重复，即有可能出现多个 A,B）。

输出格式
输出被除自己之外的所有牛认为是受欢迎的牛的数量。
题解：
先将强联通分量缩点为一个有向无环图（DAG），然后进行拓扑排序，值得注意的是，此时连通分量编号id[]递减的顺序就是topo序了，因为我们++scc_cnt是在dfs完节点i的子节点j后才判断low[u]==dfn[u]后才加的，所以降序来说，前面的节点都是该节点的后继，且该节点的前驱都在自己的前面，那么子节点j如果是强连通分量 scc_idx[j]一定小于scc_idx[i]，当一个强连通的出度为0,则该强连通分量中的所有点都被其他强连通分量的牛欢迎。但假如存在两及以上个出度=0的牛(强连通分量) 则必然有一头牛(强连通分量)不被所有牛欢迎

#include 
#include 
#include 
#include 

using namespace std;

const int N = 10010, M = 50010;

int n, m;
int h[N], e[M], ne[M], idx;
int dfn[N], low[N], timestamp;//dfs时间戳数组、能够回溯到的最早的已经在栈中的结点，时间戳变量
int stk[N], top;//栈
bool in_stk[N];//是否在栈中
int id[N], scc_cnt, Size[N];//强连通分量的编号、节点个数
int dout[N];//拓扑排序出度

void add(int a, int b)
{
    e[idx] = b;
    ne[idx] = h[a];
    h[a] = idx ++;
}

void tarjan(int u)
{
    //u的时间戳
    dfn[u] = low[u] = ++timestamp;
    //把当前点加到栈中  当前点在栈中
    stk[++top] = u,in_stk[u] = true;

    for(int i=h[u];i!=-1;i=ne[i])
    {
        int j=e[i];
        if(!dfn[j])//j点未被遍历过
        {
            tarjan(j);//继续dfs 遍历j
            //j也许存在反向边到达比u还高的层,所以用j能到的最小dfn序(最高点)更新u能达到的(最小dfn序)最高点
            low[u] = min(low[u],low[j]);
        }
        //j点在栈中  说明还没出栈 是dfs序比当前点u小的
        //则其 1要么是横插边(左边分支的点)
        //         o
        //        / \
        //       j ← u    
        //     2要么是u的祖宗节点
        //         j
        //      ↗/ 
        //       u    
        //    两种情况u的dfs序都比j大 所以用dfn[j]更新low[u]
        else if(in_stk[j])
        {
            low[u] = min(low[u],dfn[j]);//直接用j的时间戳更新u
        }
        //栈代表当前未被搜完的强连通分量的所有点
    }
    // ⭐
    // 解释一下为什么tarjan完是逆dfs序
    // 假设这里是最高的根节点fa
    // 上面几行中 fa的儿子节点j都已经在它们的递归中走完了下面9行代码
    // 其中就包括 ++scc_cnt 
    // 即递归回溯到高层节点的时候 子节点的scc都求完了
    // 节点越高 scc_id越大
    // 在我们后面想求链路dp的时候又得从更高层往下
    // 所以得for(int i=scc_cnt(根节点所在的scc);i;i--)开始

    // 所以当遍历完u的所有能到的点后 发现u最高能到的点是自己
    // 1 则u为强连通分量中的最高点,则以u为起点往下把该强连通分量所有节点都找出来
    // 2 要么它就没有环,就是一个正常的往下的点
    if(dfn[u]==low[u])
    {
        int y;
        ++scc_cnt;//强连通分量总数+1
        do
        {
            y = stk[top--];//取栈顶元素y
            in_stk[y] = false;//则y不再在栈中
            id[y] = scc_cnt;
            Size[scc_cnt] ++;//第scc_cnt个连通块点数+1
        }while(y!=u);
        //1 因为栈中越高的元素的dfs序越大,那么我们只需要把dfs序比u大的这些pop到u
        //即因为最终会从下至上回到u 所以当y==u     
        //则说明点u所在的所有强连通分量都标记了id
        //           →  u
        //          /  /
        //         /  ne1
        //         ← ne2
        //      因为ne2会在u能到的dfs序里最大的,也就是此时的栈顶
        //      那么我们就逐一pop出ne2和ne1
        //2 要么它就是一个没有环的点 则该点单点成一个连通分量
    }
}

int main()
{
    cin >> n >> m;
    memset(h,-1,sizeof h);
    while(m--)
    {
        int a,b;
        cin >> a >> b;
        add(a,b);
    }

    for (int i = 1; i <= n; i ++ )//遍历所有点，将联通分量缩点
        if (!dfn[i])
            tarjan(i);
    //统计新图中点的出度 
    for (int i = 1;i <= n; i ++ )
        for (int j = h[i];j!=-1; j = ne[j])
        {
            int k = e[j];
            int a = id[i], b = id[k];//a,b不为一个连通分量
            if (a != b) dout[a] ++ ;//a出度+1  dout[a] += i→k
        }
    int zeros = 0, sum = 0;//sum 存的所有出度为0的强连通分量的点的数量
    for (int i = 1; i <= scc_cnt; i ++ )
        if (!dout[i])//如果第i个强连通分量出度==0
        {
            zeros ++ ;
            sum += Size[i];//则加上第i个强连通分量的点的个数
            if (zeros > 1)//如果有k>1个出度为0的 则会存在k-1头牛不被所有牛欢迎
            {
                sum = 0;
                break;
            }
        }

    cout << sum;
    return 0;
}

参考博客

图论——强连通分量（Tarjan算法)
OIWiki
受欢迎的牛