算法60天训练–9.7(day2)

Problem977. 有序数组的平方

解题方法

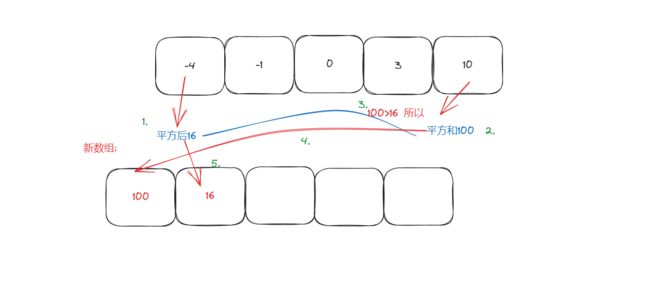
因为非递减数组,在两边的平方要么是最大,要么是最小,一定是在两边,所以这时候可以用双指针,

在数组两边定义两个指针,当左边的平方小于右边的平方,就往一个新数组放,放在最大索引处,然后左边++,同理,右边–.直到左边小于右边

复杂度

• 时间复杂度:

$O(n)$

Code

暴力

class Solution {
    public int[] sortedSquares(int[] nums) {
        int[] res = nums;
        for(int i = 0 ; i < nums.length; i++){
            res[i] *= nums[i];
        }                   
        Arrays.sort(res) ;//如果递减就  Arrays.sort(a, Collections.reverseOrder());
        return res;
    }
  
}

时间复杂度:$O(n+nlogn)$

双指针

class Solution {
    public int[] sortedSquares(int[] nums) {

        int []res = new int[nums.length]; //递增存到新数组中
        int k = nums.length-1; //新数组的索引
        
        for(int l = 0, r = nums.length-1; l <= r; ){
            if(nums[l]*nums[l] <= nums[r]*nums[r]) {
                 res[k--] = nums[r]*nums[r];
                 r --;
            }
               
            else{
                res[k--] = nums[l]*nums[l];
                l++;
            }
        }
        return res;
    }
}

时间复杂度:$O(n)$

Problem: 209. 长度最小的子数组

思路

直接暴力

两层for循环,比较简单,不做演示

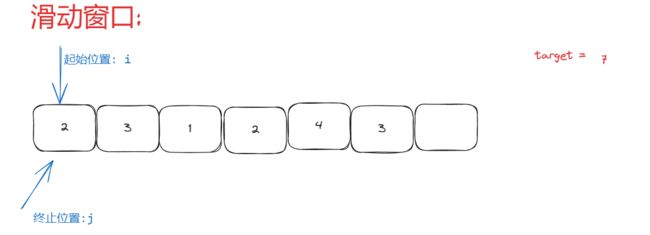
滑动窗口解法

使用一个for循环完成操作:

所谓滑动窗口,就是不断调节子序列的起始位置和终止位置,从而得出我们想要的结果

代码(java)

class Solution {
    public int minSubArrayLen(int target, int[] nums) {
							// 使用滑动窗口解法
							int i = 0;// 起始位置
							int j = 0; // 滑动窗口右端点
							int sum = 0;
							int subL = 0; //滑动窗口长度
							int result = Integer.MAX_VALUE;
							for(j = 0 ; j < nums.length; j++){
							    sum += nums[j];
							    while(sum >= target){//开始缩小窗口,注意这里是while循环，缩小滑动窗口操作是一个持续性的操作
							      subL = j - i + 1;
							      result = Math.min(result,subL);
							    		sum = sum - nums[i];
							      i++;
							    }
							    
							}
							return result == Integer.MAX_VALUE ? 0 : result; // 注意有没有被赋值
    }
}

时间复杂度：$O(n)$
空间复杂度：$O(1)$

Problem: 59. 螺旋矩阵 II

思路

本题无非就是遍历二维数组,一层层向里遍历,但是不统一规定遍历每一条边的边界,会非常的混乱

所以本题采用循环不变量,对于判断每次螺旋的边界麻烦,不妨都采取左闭又开的原则

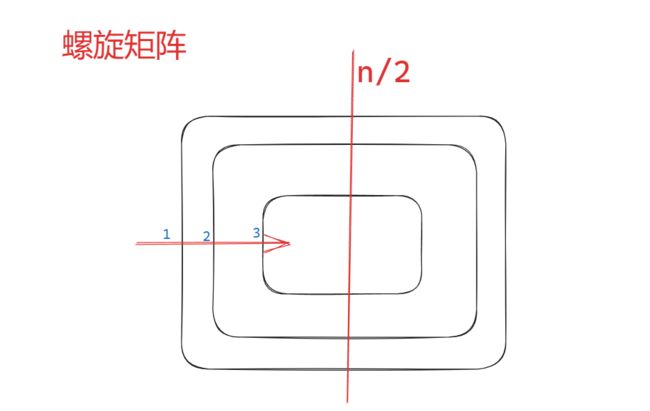
第一个不太好理解的地方就是为什么循环n/2圈?是因为最后循环结束的时候StartX一定是在相对于第一条边中间的位置,那么循环了多少圈就可以由这个点对两边的竖边的条数进行分割.两边的条数一定是相等的,有就是转了多少圈.

由图可以发现,转了3圈

第二个地方就是左开右闭,每到一个节点就进入下一个边的循环.

在每个圈数结束后,更新起点,横纵坐标都加一.startX+1;startY+1

如果n/2等于一,说明最中间有单独的数,直接单独赋值

代码:

class Solution {
    public int[][] generateMatrix(int n) {
        int loop = 0; // 控制循环次数
        int [][] res = new int[n][n];
        int start = 0; //每次循环的开始点(start, start)
        int count = 1; //定义填充数字
        int i,j;

        while(loop ++ < n/2){//判断边界后,loop从1开始

        //模拟上侧从左到右
        for(j = start; j<n-loop; j++){// n-loop 是为了左闭又开
            res[start][j] = count++;
        }

        //模拟右侧从上到下
        for(i = start; i < n-loop; i++){
            res[i][j] = count++;
        }
        
        for(;j>=loop;j--){//此时loop等于一,startX+1的位置
            res[i][j] = count++;
        }


        // 模拟从下到上
        for(;i>=loop;i--){ //此时loop等于一,startY+1的位置
            res[i][j] = count++;
        }
        start++;
        }
        if(n%2 == 1){
            res[start][start] = count;
        }
        return res;
    }
}

时间复杂度 O(n^2): 模拟遍历二维矩阵的时间
空间复杂度 O(1)