基于深度学习算法的轴承故障自主分类

1. 要求

轴承有3种故障：外圈故障，内圈故障，滚珠故障，外加正常的工作状态。如表1所示，结合轴承的3种直径（直径1,直径2,直径3），轴承的工作状态有10类：

                        表1 轴承故障类别

	外圈故障	内圈故障	滚珠故障	正常
直径1	1	2	3	0
直径2	4	5	6
直径3	7	8	9

实验包含以下两个文件：

1.train.csv，训练集数据，1到6000为按时间序列连续采样的振动信号数值，每行数据是一个样本，共792条数据，第一列id字段为样本编号，最后一列label字段为标签数据，即轴承的工作状态，用数字0到9表示。

 2.test_data.csv，测试集数据，共528条数据，除无label字段外，其他字段同训练集。  总的来说，每行数据除去id和label后是轴承一段时间的振动信号数据，选手需要用这些振动信号去判定轴承的工作状态label。  注意：同一列的数据不一定是同一个时间点的采样数据，即不要把每一列当作一个特征

采用CNN、RNN等深度学习算法，实现对具有序列特性的轴承故障样本的自主分类。

要求：（1）利用Python sklearn安装包，调用CNN、RNN算法，对轴承故障样本实现自主分类。

（2）表格输出训练集、测试集分类精度、DICE, Jarccard 参数值

2. 过程

本次实验主要通过卷积神经网络来进行处理，可以直接通过python中的keras神经网络库来进行搭建。首先读取训练集文件，然后再对其进行处理，产生生成器，其中的label标签数据转换成把标签转成OneHot，后续通过然后使用 keras的fit_generator进行调用，其结果如下：

图1 训练样本生成器

图2 处理后的训练集特征值及标签（部分）

同样，测试集样本也作处理产生生成器，结果如下：

图3 处理后测试集生成器数据（部分）

然后开始建立模型，通过调用keras库里的models来进行构造，使用 Sequential() 实现全连接网络，网络模型搭建完后，需要对网络的学习过程进行配置，否则在调用 fit 或 evaluate 会抛出异常。我使用compile (loss='categorical_crossentropy', optimizer=Adam(0.0002), metrics=['accuracy'])来完成配置。

产生的一个模型如下：

图4 打印模型

导入训练后的模型来实现分类，通过model.predict_generator()语句来对测试集中的数据进行预测，其尺寸与结果如下图：

图5 测试集文件中的数据预测结果

接下来为了进一步探究该模型的好坏，首先读取训练集数据后，将其转换成numpy，取出head，然后提取其中属于特征值的列提取出来，再将其中的label值单独提取出来，然后通过sklean中的train_test_split()函数将训练集中的数据进行分割，其中测试集占0.4。处理完毕后，通过模型进行预测，其相关结果如下：

图6 预测精度

图7 混淆矩阵

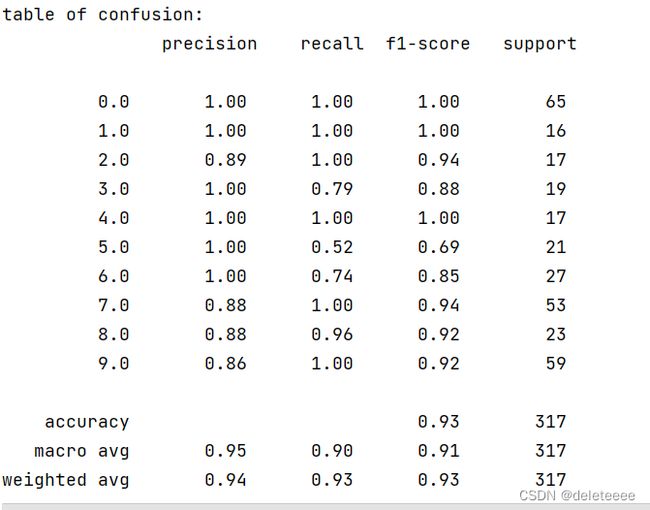
图8 confusion 表

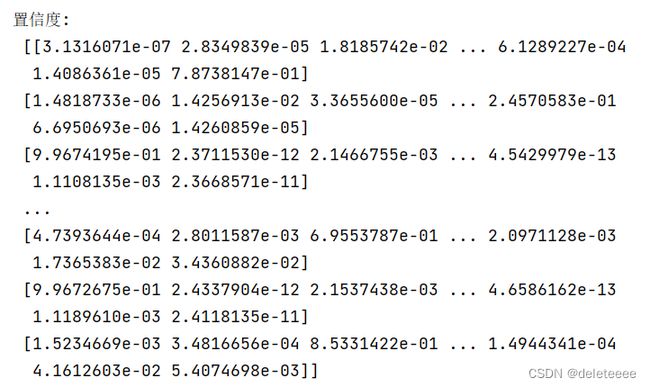
图9 测试集置信度

通过precision_recall_curve()函数得到Precision, Recall值，利用roc_curve()得到FPR, TPR值，绘制如下曲线：

图10 PR曲线

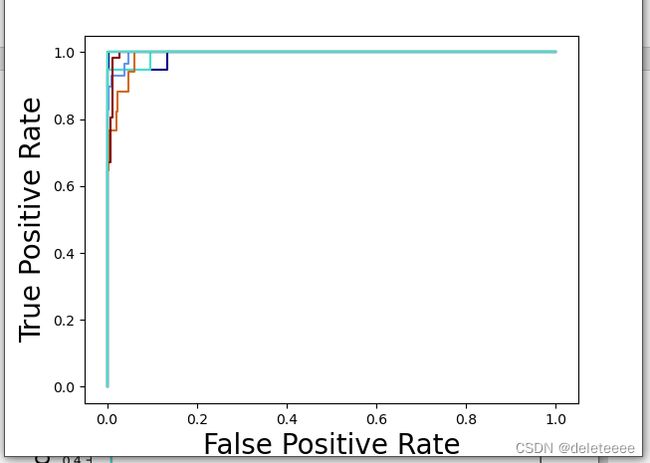
图11 ROC曲线

图12 相关指标

再多次运行程序，结果如下：

图13

图14

然后我增加了数据迭代次数epochs值，再次训练模型，然后通过验证，其结果如下：

图15 调整后的精度和混淆矩阵

图16 调整后的总体结果

可以发现精度上升了很多，说明该模型分类结果较为准确

3. 结果与分析

在上述实验过程中，我主要实现了对测试集文件进行分类以及对分类模型进行评估。在构建卷积神经网络并进行训练后，得到了图5所示的结果。然而，由于我不清楚其真实标签，因此无法判断模型的好坏。因此，我对训练集的文件进行处理，将其分割成训练样本和测试样本，然后进行评估。经过验证后，其结果如图6至图12所示。我通过精度、汉明距离、Jaccard值、AUC大小等参数来作为评估指标。从中可以看出准确率和召回率的调和平均数F1-score的值总体较大，更能说明模型的性能较好。除此之外，我还绘制了它们的ROC曲线和PR曲线。从曲线中我们也可以更加直观地看出ROC曲线靠近左上角，PR曲线靠近右上角，这说明该分类模型较好。

训练集和测试集的精度都超过了90%，但出现了训练集的精度低于测试集的异常。经过多次运行程序，在图13和图14中可以看出训练集的精度大于测试集的，并且都达到了90%以上。出现异常的结果可能是由于我在分割样本时采用了随机分割，所以可能会选取到不合适的样本导致异常。为了提高分类精度，我增加了epochs值，通过多次迭代后产生了新的模型。通过验证可以看出，模型性能得到了优化，分类效果更加好了。由此可以判断它对于测试集文件的自主分类也实现较好。