编译原理与技术（二）——词法分析（三）词法分析器的构造

词法分析器就是NFA或DFA，这从前面可以看出。

虽然DFA比NFA快，但其特性少，而NFA则特性丰富。所以在实际应用中，NFA作为词法分析器反而应用更加广泛。像Python与Ruby的RE模块都是NFA的。

本节重点讲如何构造一个词法分析器，即如何构造一个NFA、DFA与化简的DFA。

一、NFA的构造

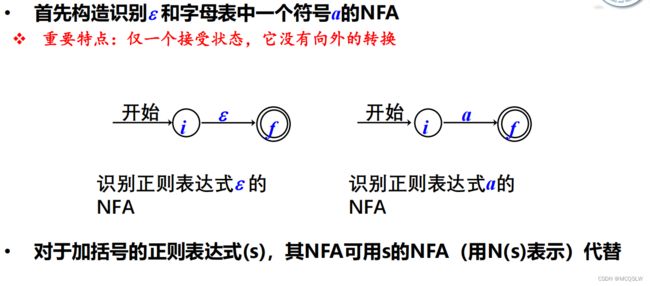
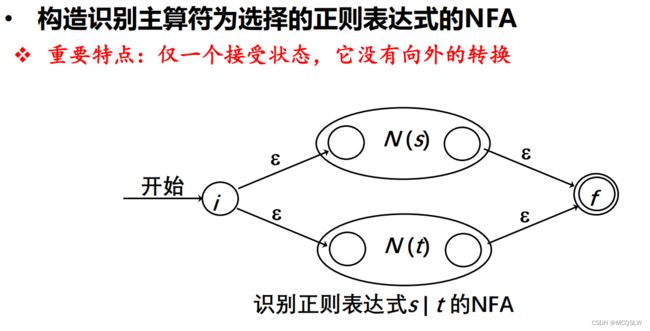
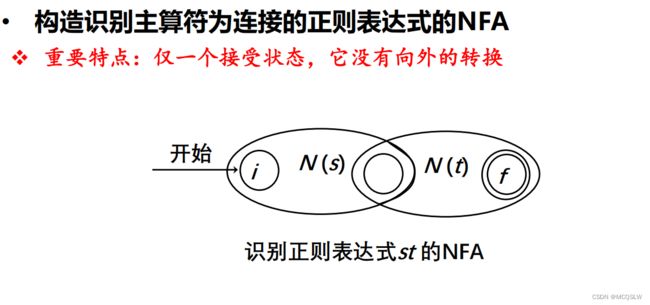
下面介绍一个构造NFA的算法——语法制导的构造算法。

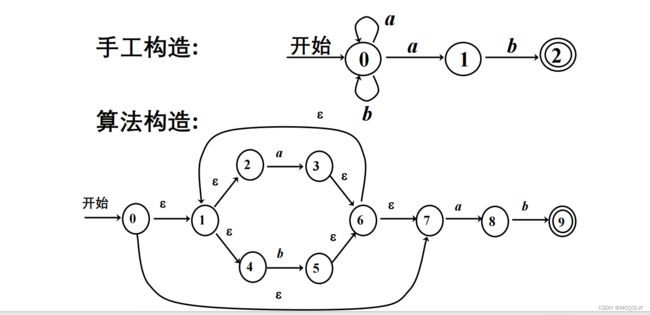
按如上方法与顺序便可构造出一个NFA。

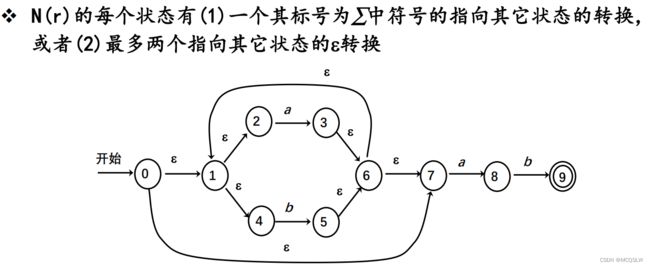
由上述方法产生的NFA具有下面三个性质。

 

下面将手工构造的NFA与算法构造的NFA做一个直观对比。

 

现在，我们已经掌握了由正则表达式构造出NFA的形式化方法。

二、DFA的构造

 DFA由NFA推出，这里介绍推出的一种方法——子集法。

换言之，子集法就是将NFA的转换结果（多个状态）合并为一个状态。

举个例子。

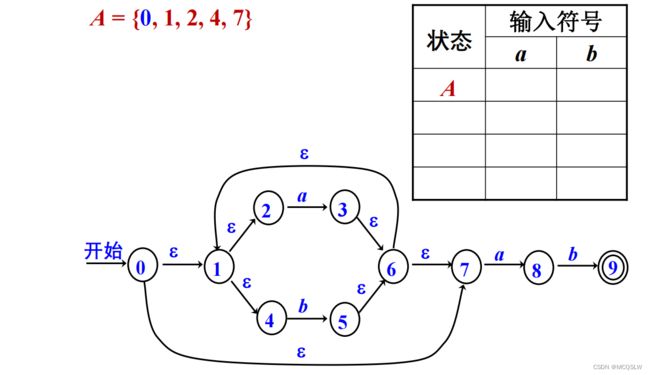
  求初始状态0的ε-闭包A={0，1，2，4，7}，A是DFA的初始状态。

对A施以转换函数并配以输入字符后，求得每个输入字符下的ε-闭包：

接受字符“a”——>{1，2，3，4，6，7，8}

接受字符"b"——>{1，2，4，5，6，7}

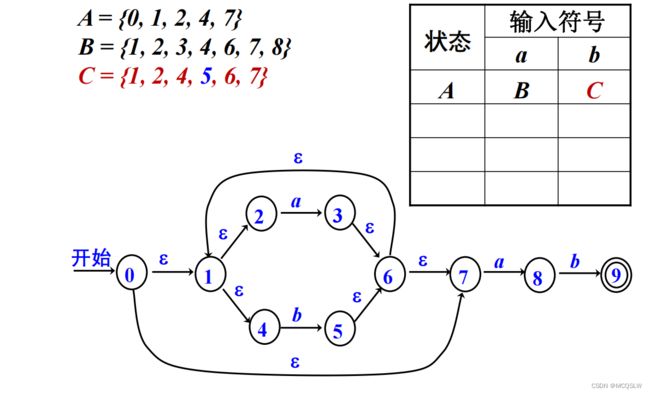
由于得到的两个集合是新的（当前DFA中没有），则将它们分别作为集合加入DFA中，并分别取名状态B与状态C。

 状态B与状态C显然会在转换函数的作用下继续接收字符去匹配，所以仿照上面的步骤继续构造，直至没有新的状态出现。

含有原来NFA的终结状态的集合就是当前DFA的终结状态，上图中的状态D就是当前DFA的终结状态。

上图中的表就是DFA，将其用图表示出来。

 

现在，我们掌握了由NFA得出DFA的形式化方法。

我们发现，上图中的DFA是没有ε（空串）作为匹配字符的，实际上，DFA是不可能把ε（空串）作为匹配字符的。

 三、DFA的化简

在上图的DFA中，我们发现，状态A和状态C能够匹配的字符串一样，即对于任意一个串，使得状态A与状态C各自经过该串要么都到达接受状态，要么都不到达接受状态。

所以，我们完全可以把这样的A与C合并为一个状态A，那么我们可以得到下面的DFA。

这个DFA比原来的DFA更加精简，执行效率与速度会更好。

理论证明，一个DFA可以存在许多与其等价的形式，即有许多DFA虽然长得不一样，但本质是一样的。那么问题来了，如何判定两个DFA是否等价呢？

理论证明，任何一个DFA都一定有唯一确定的最简的DFA，即等价的DFA都一定等价于唯一一个状态数最少的DFA，这个DFA就被称为最简DFA。而如何判定两个DFA是否等价，就只需要判定这两个DFA各自对应的最简DFA是否一样。若一样则说明这两个DFA是等价的，否则就不是等价的。

而将一个DFA转换成最简DFA的过程就是DFA的化简，下面提供一种方法。

经过第一次分解后，我们发现状态B匹配字符“b”后到达终结状态，所以将其分离出去。

我们发现，A与C的匹配情况完全一致，所以分解结束。

上面的最简DFA就是下图：

 

四、总结

正则表达式是匹配词法单元的工具。

有限自动机是形式化描述匹配过程的工具。

因此用正则表达式去匹配词法单元可以通过NFA或DFA。

而DFA由NFA推出，NFA由正则表达式推出，即DFA与推出其的NFA等价，NFA与推出其的正则表达式等价，所以DFA与构造它的正则表达式等价。

而DFA的形式有许多，区别两个DFA的方法是看这两个DFA对应的最简DFA是否一样，这也就引出了判定两个正则表达式是否等价的方法——看这两个正则表达式各自对应的最简DFA是否一样。

参考资料：

 [1]USTC 编译原理和技术 2023 (ustc-compiler-principles.github.io)