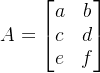蓝桥杯训练-矩阵乘法（day13）

一、题目

给定一个N阶矩阵A，输出A的M次幂（M是非负整数）

输入：

       第一行是一个正整数N，M（，），表示矩阵的阶数和要求的幂数。

      接下来N行，每行N个绝对值不超过10的非负整数，描述矩阵A的值。

输出：

       输出N行，每行N个整数，表示A的M次幂所对应的矩阵，相邻的数之间用空格隔开。

输入：

A=

1 2 

3 4

输出A的2次幂：

7 10

15 22

二、例子

输入：

2 2 

1 2 

3 4

输出：

7 10

15 22

三、解析

A,B,C是三个矩阵，若AxB=C，矩阵C的第i行j列元素=矩阵A的第i行元素与矩阵B的第j列对应元素乘积之和。

例：

,, 求 

四、涉及的知识 

• 函数定义；for循环：蓝桥杯训练-序列求和（day7）-CSDN博客
• if语句；if __name__ = '__main__':蓝桥杯训练-字符串对比（day8）-CSDN博客

五、python代码及逐行解析

def solve(N,rect1,rect_ans):     #遍历rect1和rect_ans的元素，计算矩阵相乘的结果，将结果存储在rect2中
    rect2 = [[0 for _ in range(N)] for _ in range(N)]#初始化一个二维数组rect2用来存储计算结果，例：N=2,M=2时，rect2 = [[0, 0], [0, 0]]
    for i in range(N):           #遍历矩阵的行
        for j in range(N):       #遍历矩阵的列
            for n in range(N):
                rect2[i][j] += rect1[i][n] * rect_ans[n][j]    #计算每行矩阵相乘的结果
    return rect2                                               #返回计算结果rect2
if __name__ == '__main__':
    N,M = map(int,input().split())   #输入矩阵的阶数N和要求的幂M
    rect1 = [[] for _ in range(N)]   #初始化一个二维数组rect1，用于存储输入的矩阵,例：N=2时，rect1 = [[], []]
    for i in range(N):               #遍历矩阵的行和列，输入第i行j列的数据，将结果添加到rect1
        arr = input().split()
        for j in range(N):
            rect1[i].append(int(arr[j])) #输入第i行第j列的数据
    if M > 0:                            #矩阵的幂大于零，计算矩阵相乘的结果，并将计算结果存入rect_ans中
        rect_ans = rect1
        for i in range(M-1): 
            rect_ans = solve(N,rect1,rect_ans)
    else:                   #矩阵的幂等于零，输出单位矩阵
        rect_ans = [[0 for _ in range(N)] for _ in range(N)]#初始化一个二维数组用来存储单位矩阵
        for i in range(N):  #利用循环，将单位矩阵的值赋值给rect_ans
            rect_ans[i][i] = 1
    for i in range(N):      #用循环遍历矩阵行和列，输出rect_ans中的元素
        for j in range(N):
            print(rect_ans[i][j],end=' ')
        print()

运行结果：

2 2
1 2 
3 4
7 10 
15 22 

------------------------

2 0
1 2
3 4
1 0 
0 1