Leetcode——打家劫舍1,2,3
1. 打家劫舍1 / 按摩师问题
一个有名的按摩师会收到源源不断的预约请求,每个预约都可以选择接或不接。在每次预约服务之间要有休息时间,因此她不能接受相邻的预约。给定一个预约请求序列,替按摩师找到最优的预约集合(总预约时间最长),返回总的分钟数。
示例 1:
输入: [1,2,3,1]
输出: 4
解释: 选择 1 号预约和 3 号预约,总时长 = 1 + 3 = 4。
示例 2:
输入: [2,7,9,3,1]
输出: 12
解释: 选择 1 号预约、 3 号预约和 5 号预约,总时长 = 2 + 9 + 1 = 12。
示例 3:
输入: [2,1,4,5,3,1,1,3]
输出: 12
解释: 选择 1 号预约、 3 号预约、 5 号预约和 8 号预约,总时长 = 2 + 4 + 3 + 3 = 12。
(1)递归
直接递归:
- 最简单的想法就是,遍历所有可能的情况,找出可能的最大值。
- 递归函数返回值为从第i个房屋开始包括第i个房屋在内的房屋所能偷窃的最大值
- 递归函数需要传入的参数为房屋位置i以及标记issteal标记第i-1个房屋是否被偷过
- 递归函数需要做的仅仅是根据i-1个房屋是否偷过决定能否偷第i个房屋,而第i+1及之后的房屋可以通过递归计算得到
这种dfs穷举法的时间复杂度是指数级的,对于长度范围为100的测试用例是肯定会超TLE的。
class Solution {
public int rob(int[] nums) {
return dfs(nums, 0, false);
}
/* 返回第i个房屋及之后能偷窃到的最大值,issteal标志第i - 1个房屋是否偷窃 */
int dfs(int[] nums, int i, boolean issteal) {
/* i越界,没房屋可供偷窃,只能空手而归了>_< */
if (i >= nums.length)
return 0;
/* 前一个偷过了,那这个就不能偷了!去下一家看看~ */
else if (issteal)
return dfs(nums, i + 1, false);
/* 前一个没偷过,那么这个可偷可不偷,两者取大的那个 */
else
return Math.max(dfs(nums, i + 1, true) + nums[i], dfs(nums, i + 1, false));
}
};
记忆化递归:
class Solution {
//map表示从第start个房子开始,偷到最后一个房子的最大值
Map<Integer,Integer> map=new HashMap<>();
public int rob(int[] nums) {
if(nums.length==0)
return 0;
return dfs(nums,0);
}
public int dfs(int[] nums,int start)
{
if(start>=nums.length)
return 0;
//查表
if(map.containsKey(start))
return map.get(start);
//分两种情况
//1.偷第start个房子,然后只能从第start+2个房子开始偷
int hasFirst=nums[start];
hasFirst+=dfs(nums,start+2);
//2.不偷第start个房子,从第start+1个房子偷
int noFirst=0;
noFirst+=dfs(nums,start+1);
//取两种情况的最大值
int ans=Math.max(hasFirst,noFirst);
//把从第start个房子开始,偷到最后一个房子的最大值ans记录下来
map.put(start,ans);
return ans;
}
}
其实,这个就是转移方程
int ans=Math.max(hasFirst,noFirst);
只需要增加一个数组把计算过之后的记录保存下来,在每一次DFS进入时候判断这个值是否被计算过,就是动态规划了。
动态规划并没有优化时间复杂度,它的优化就是通过保存之前的计算过程把树形计算剪枝成线性计算。
(2)DP处理
本题既有爬楼梯的影子,也有最长连续子序列和的影子。
解答本题的关键,在于理解题目表述中,预约服务要有休息时间的含义。其意思不仅在于,不能接收相邻的预约这么简单。结合要找预约时间最长,我们要能够分析出,最优预约集合中的最后一个元素,不是nums[nums.size()-1] 就是 nums[nums.size()-2]
举个例子,对于任意预约序列[a0,a1,a2,a3,…,an-3,an-2,an-1]来说,其符合题目要求的最优预约集合中,最后一个元素一定出自 an-2 或 an-1。如果可以理解到这个层面,本题就可以成功转化为一个普通的一维动态规划问题了。即我们的目标是,找到以an-2 和 an-1 结尾的各自最大预约,然后比较他俩谁更大,即可。更进一步,要找an-2结尾的各自最大预约,就是要找an-4 和 an-5的最大预约(因为不能接收相邻预约嘛,所以要隔着找)
由此,就可以清楚了解到其子问题。
思路解释:
-
(1)base case
基础问题比较简单,因为其不接受相邻预约,所以基础问题就是只有1个预约时,以这个预约结尾的最优预约时间就是:
dp[0] = nums[0];
如果有两个预约,以后一个预约结尾的最优预约时间就是:
dp[1] = nums[1]; -
(2)确定状态
状态就是子问题中变化的量,经过上面的分析,子问题n就是,以采纳n号元素作为最优预约结尾的最优预约时长。
所以说,这个状态就是以 第几个预约作为最优预约的结尾元素。 -
(3)确定选择
选择就是导致状态改变的原因,对于子问题i,我们一定要把nums[i]加入到当前子问题的最优预约中,所以为达成这个子问题目的,
选择就是,从前面i-2个子问题中(要排除掉第i-1个,因为不接受相邻),选择预约时长最长的组合加进来 -
(4)确定dp数组含义
其实这个确定含义的工作,在题目理解的部分已经做过了。
dp[i]的含义就是,对于nums的前i+1个元素组成的子预约集合中,以nums[i]作为最优预约集合结尾元素时,最优预约时间长度。
这么说不是很好理解,举个例子。
对于数组[2,7,9,3,1]来说,其dp[3] 表示 在[2,7,9,3]这个子数组中,以3这个元素作为最优预约集合结尾元素时,其最优预约的时间长度。
以3结尾时,最优预约集合为[7,3],所以dp[3] = 10。
同理,dp[4],就是表示在[2,7,9,3,1]这个子数组中,以1这个元素作为最优预约集合结尾元素时,其最优预约的时间长度。
以1结尾时,最优预约集合为[2,9,1],所以dp[4] = 12. -
(5)写状态转移方程
清楚的理解了每一步后,状态转移方程就很好写了。
首先dp[0] = nums[0]
dp[1] = nums[1]
对于i >= 2来说, dp[i] = max(dp[0],dp[1],dp[2],…,dp[i-3],dp[i-2]) + nums[i];
同理,上边的方程中没有dp[i-1] 是因为不能取相邻。
相信到这里,大家都很容易理解这个方程的含义了。
同时,我们不需要额外的循环去实现这个max,我们只需要通过一个变量来保存即可。
class Solution {
public int massage(int[] nums) {
if(nums.length==0) //特殊情况
return 0;
else if(nums.length==1){ //特殊情况
return nums[0];
}
else{
int[] dp = new int[nums.length];
dp[0] = nums[0];
dp[1] = Math.max(nums[0],nums[1]);
int max = dp[1]; **//max用于记录过往的最大值
for(int i=2;i<nums.length;i++){
dp[i] = Math.max(dp[i-1], dp[i-2] + nums[i]); // 上一个dp[i-1]最大值与前一个dp[i-2]+nums[i]相比较,避免相邻情况。
max = Math.max(max,dp[i]);
}
return max;
}
}
}
优化:
一般的动态规划 。 本来应该是定义dp数组的。但是在这里 n位置的结果,只需要n-1和 n-2的结果就可以推出来,所以只需要保存两个结果。first second的作用和dp数组一样。
class Solution {
public int massage(int[] nums) {
int first=0;
int second=0;
for(int i:nums){
int temp=second;
second=Math.max(second,first+i);
first=temp;
}
return second;
}
}
2. 打家劫舍2
(1)分两次递归(超时)
class Solution {
public int rob(int[] nums) {
if (nums == null || nums.length == 0)
return 0;
int len = nums.length;
if (len == 1)
return nums[0];
return Math.max(dfs1(nums, 0, false), dfs2(nums, 1, false));
}
//比较0 -> len-1 和 1 -> len 之间哪个更大
int dfs1(int[] nums, int i, boolean issteal) {
if (i >= nums.length - 1)
return 0;
else if (issteal)
return dfs1(nums, i + 1, false);
else
return Math.max(dfs1(nums, i + 1, true) + nums[i], dfs1(nums, i + 1, false));
}
int dfs2(int[] nums, int i, boolean issteal) {
if (i >= nums.length)
return 0;
else if (issteal)
return dfs2(nums, i + 1, false);
else
return Math.max(dfs2(nums, i + 1, true) + nums[i], dfs2(nums, i + 1, false));
}
}
(2)DP(分为两个单排)
- 与上一个打家劫舍1 唯一的区别是此题中的房间是环状排列的(即首尾相接),而 198题中的房间是单排排列的;而这也是此题的难点。
- 环状排列意味着第一个房子和最后一个房子中只能选择一个偷窃,因此可以把此环状排列房间问题约化为两个单排排列房间子问题:

所以我们可以: - 比较0 -> len-1 和 1 -> len 之间哪个更大
class Solution {
public int rob(int[] nums) {
if (nums == null || nums.length == 0)
return 0;
int len = nums.length;
if (len == 1)
return nums[0];
return Math.max(robAction(nums, 0, len - 1), robAction(nums, 1, len));
}
int robAction(int[] nums, int start, int end) {
int pre = 0, cur = 0, tmp = 0;
for (int i = start; i < end; i++) {
tmp = cur;
cur = Math.max(cur, pre + nums[i]);
pre = tmp;
}
return cur;
}
}
3. 打家劫舍3
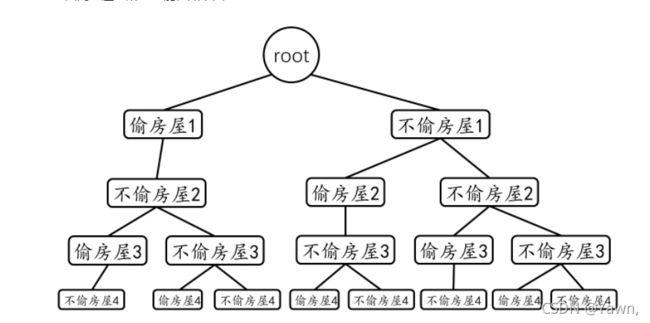
(1)暴力递归
爷爷节点获取到最大的偷取的钱数呢
- 首先要明确相邻的节点不能偷,也就是爷爷选择偷,儿子就不能偷了,但是孙子可以偷
- 二叉树只有左右两个孩子,一个爷爷最多 2 个儿子,4 个孙子
根据以上条件,我们可以得出单个节点的钱该怎么算
- 4 个孙子偷的钱 + 爷爷的钱 VS 两个儿子偷的钱 哪个组合钱多,就当做当前节点能偷的最大钱数。这就是动态规划里面的最优子结构
class Solution {
public int rob(TreeNode root) {
if (root == null)
return 0;
int money = root.val;
if (root.left != null) {
money += rob(root.left.left) + rob(root.left.right);
}
if (root.right != null) {
money += rob(root.right.left) + rob(root.right.right);
}
//四个孙子+爷爷 vs 两个儿子
//计算了root的四个孙子(左右孩子的孩子)为头结点的子树的情况,又计算了root的左右孩子为头结点的子树的情况,计算左右孩子的时候其实又把孙子计算了一遍。
//这里也计算了 两个儿子的情况,所以存在重复计算
return Math.max(money, rob(root.left) + rob(root.right));
}
}
(2)记忆化递归(备忘录算法)
- 解法一种速度太慢的问题,经过分析其实现,我们发现爷爷在计算自己能偷多少钱的时候,同时计算了 4 个孙子能偷多少钱,也计算了 2 个儿子能偷多少钱。
- 这样在儿子当爷爷时,就会产生重复计算一遍孙子节点。
class Solution {
public int rob(TreeNode root) {
Map<TreeNode, Integer> memo = new HashMap<>();
return robAction(root, memo);
}
public int robAction(TreeNode root, Map<TreeNode, Integer> memo) {
if (root == null)
return 0;
if (memo.containsKey(root)) //如果该节点已计算过,直接返回
return memo.get(root);
int money = root.val;
if (root.left != null) {
money += robAction(root.left.left, memo) + robAction(root.left.right, memo);
}
if (root.right != null) {
money += robAction(root.right.left, memo) + robAction(root.right.right, memo);
}
int res = Math.max(money, robAction(root.left, memo) + robAction(root.right, memo));
memo.put(root, res);
return res;
}
}
(3)状态标记递归(有点像 dp)
每个节点可选择偷或者不偷两种状态,根据题目意思,相连节点不能一起偷
- 当前节点选择偷时,那么两个孩子节点就不能选择偷了
- 当前节点选择不偷时,两个孩子节点只需要拿最多的钱出来就行(两个孩子节点偷不偷没关系)
我们使用一个大小为 2 的数组来表示 int[] dp= new int[2] 0 代表不偷,1 代表偷
任何一个节点能偷到的最大钱的状态可以定义为
- 当前节点选择不偷:当前节点能偷到的最大钱数 = 左孩子能偷到的钱 + 右孩子能偷到的钱
- 当前节点选择偷:当前节点能偷到的最大钱数 = 左孩子选择自己不偷时能得到的钱 + 右孩子选择不偷时能得到的钱 + 当前节点的钱数
class Solution {
public int rob(TreeNode root) {
int[] res = robAction1(root);
return Math.max(res[0], res[1]); //选择是否偷当前节点的最大值
}
public int[] robAction1(TreeNode root) {
int res[] = new int[2];
if (root == null)
return res;
int[] left = robAction1(root.left);
int[] right = robAction1(root.right);
//不偷当前节点 与 偷当前节点
res[0] = Math.max(left[0], left[1]) + Math.max(right[0], right[1]); //当前节点选择不偷 = 左孩子能偷到的钱 + 右孩子能偷到的钱
res[1] = root.val + left[0] + right[0]; //当前节点选择偷 = 左孩子选择自己不偷时能得到的钱 + 右孩子选择不偷时能得到的钱 + 当前节点的钱数
return res;
}
}