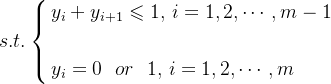分别用线性规划和动态规划求解打家劫舍问题（力扣198）

写在前面：

1. 本人是只挣扎在数模海洋的小可怜，最近同时学线性规划和动态规划，于是就有了这篇博客

2. 编程使用matlab

3. 动态规划解法参考 数学建模清风动态规划课程https://www.bilibili.com/video/BV1tp4y167c5

打家劫舍问题描述：

你是一个小偷，现在有一排相邻的房屋等着你去偷窃。这些房子装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。给定一个代表每个房屋存放金额的正整数数组，计算你不触动警报装置的情况下，一夜之内能够偷窃到的最高金额。（不考虑偷窃时间）

示例1：

输入：[1,2,3,1,3]

输出：7

解释：偷窃1号、3号、5号房屋，偷窃到的最高金额=1+3+3=7。

示例2：

输入：[2,7,2,3,8]

输出：15

解释：偷窃2号、5号房屋，偷窃到的最高金额=7+8=15。

解法一：线性规划

设有间房屋，每间房屋存放的金额记为，引入一套0-1变量，表示偷第间房屋，表示不偷第间房屋。

则目标函数写为

根据题目“如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警”，则小偷不能偷相邻两间房屋，即相邻两个0-1变量不能同时取1，故约束条件写为：

综上，线性规划的数学模型为：

 代码如下：

（如果不懂可以在命令行键入doc optimproblem查看帮助文档）

function [fval,ind]=djjs(v)
m=length(v);  % 共m间房屋
prob=optimproblem("ObjectiveSense","max");  % 创建一个求最大值的优化问题
y=optimvar('y',1,m,'Type',"integer","LowerBound",0,"UpperBound",1);  % 决策变量，规模1*m，0-1变量
prob.Objective=sum(y.*v);  % 目标函数
con=optimconstr(m-1);  % 创建空约数集合
for i=1:m-1
    con(i)=y(i)+y(i+1)<=1;
end  % 填写约束
prob.Constraints.con=con;  % 将约束集合纳入问题
[sol,f]=solve(prob);  % 求解
fval=f;
ind=sol.y;
end

运行时在命令行键入：

clear
v=[1,2,3,1,3];
[fval,ind]=djjs(v)

运行结果：

 解法二：动态规划

ps：动态规划我是跟着清风老师的视频学的，在这里我不讲这一算法的内容。下面的思考步骤（注意，我说的是思考步骤）是我根据清风的视频加上自己的学习体验总结的，看着比较啰嗦但是我自己这样思考的话有助于求解问题。

（1）定义原问题和子问题

原问题：从全部间房屋偷窃得到的最高金额

子问题：从前间房屋偷窃得到的最高金额

（2）定义状态和最值函数

状态：前间房屋

最值函数：从前间房屋偷得的最高金额

（3）描述dp数组

本问题中dp数组是一维数组，设数组下标为，从1取到，对应数组值表示 从前间房屋中偷得的最高金额，即各个子问题的解。数组最后一个值，即时，即原问题的解。

（4）状态转移方程

思考状态转移方程时，可以问自己这么几个问题：哪些状态可以转移到当前状态？从哪个状态转移会达到最优？前后状态最值函数间的关系式怎么构建？

易知，从状态和状态可以转移到当前状态。如果从状态转移，为不触发报警器则第间房屋不能偷，故有；如果从状态转移，为使偷得金额最大则需偷第间房屋，故有。但是我们并不清楚从哪个状态转移会使达到最大，故状态转移方程写为：

（可能有人会有疑问，如果从状态转移但是第间房屋并没有偷，是不是可以有？其实这种情况等同于从状态转移：，所以不应重复计算）

关于状态转移方程，也可以这样构造一个场景思考：

小偷到第间房屋时，如果第间房屋已经偷过， 为不触发报警器则第间房屋不能偷，故有；如果第间房屋没有偷过，为使偷得金额最大则需偷第间房屋，故有。故也可得出状态转移方程：

（5）边界条件

本题的边界条件有两个：

（6）编程求解dp数组

基于已得到的状态转移方程、边界条件，跑循环逐个求解dp数组的值。

代码如下：

function fval=djjs(v)
m=length(v);  % 共有m间房屋
if m==1  % 出口1：如果只有1间房，直接返回v(1)
    fval=v(1);
elseif m==2  % 出口2：如果只有2间房，直接返回v(1)和v(2)中的较大值
    fval=max(v(1),v(2));
else  % 出口3
    dp=v(1)*ones(1,m);  % 定义dp数组
    dp(2)=max(v(1),v(2));  % 边界条件
    for x=3:m  % 顺序、循环求解
        dp(x)=max(dp(x-1),dp(x-2)+v(x));  % 状态转移方程
    end
    fval=dp(m);
end
end

运行时在命令行键入以下代码即可：

clear
v=[1,2,3,1,3];
fval=djjs(v)