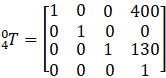SCARA机器人运动学分析--Matlab
设SCARA机器人初始参数如下:
a1=200,a2=200; d1=200,d2=30,d4=100;
 SCARA机器人简图及各连杆坐标系建立
SCARA机器人简图及各连杆坐标系建立
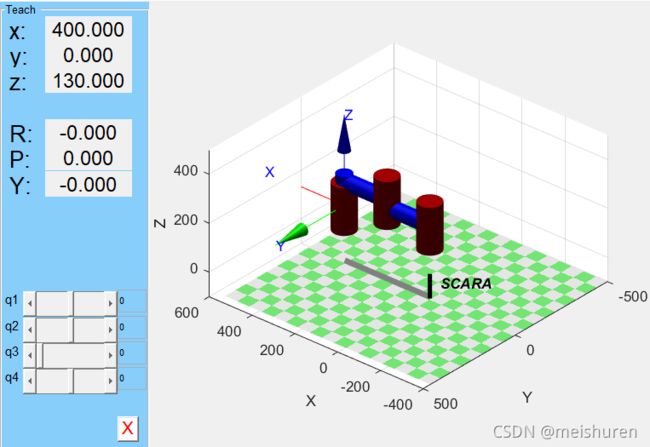
当θ1=0,θ2=0,θ4=0,d3=0时,即SCARA机器人在初始状态下时,
利用Matlab计算机器人坐标系{4}相对于坐标系{0}的位姿,有:
p1=0;p2=0;p3=0;p4=0; %"p"表示关节角theta
d1=200;d2=30;d3=0;d4=-100; %“d”为连杆偏距
a0=0;a1=200;a2=200;a3=0; %“a”为连杆长度
A1=[cosd(p1),-sind(p1),0,0;sind(p1),cosd(p1),0,0;0,0,1,d1;0,0,0,1];
A2=[cosd(p2),-sind(p2),0,a1;sind(p2),cosd(p2),0,0;0,0,1,d2;0,0,0,1];
A3=[1,0,0,a2;0,1,0,0;0,0,1,d3;0,0,0,1];
A4=[cosd(p4),-sind(p4),0,0;sind(p4),cosd(p4),0,0;0,0,1,d4;0,0,0,1];
A5=A1*A2*A3*A4;
A5运算可得:
- 此时,SCARA机器人位姿可利用Matlab机器人工具箱表示出来:
代码如下:
%[]中参数依次为 关节角theta 连杆偏距d 连杆长度a 连杆扭转角alpha 关节变量偏移量offset
L1=Link([0 200 0 0],'modified');
L2=Link([0 30 200 0],'modified');
L3=Link([0 0 200 0 1],'modified');
L4=Link([0 -100 0 0],'modified');
SCARA=SerialLink([L1 L2 L3 L4], 'name', 'SCARA');
%机器人各关节限位设置
SCARA.qlim=[-125*pi/180 125*pi/180;-140*pi/180 140*pi/180;0 200;-2*pi 2*pi];
SCARA.plot([0 0 0 0], 'workspace',[-400 600 -500 500 -100 500]);
SCARA.teach
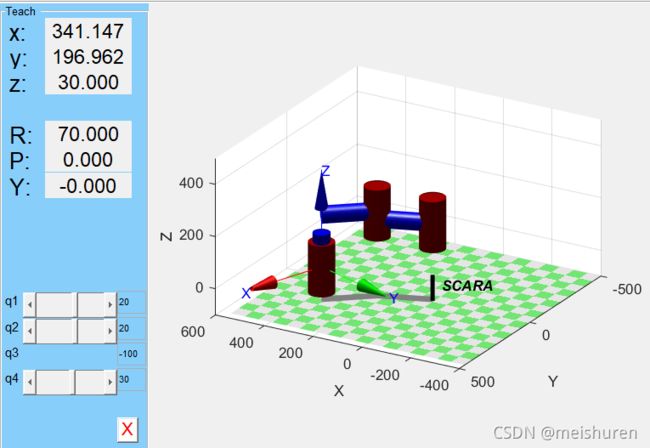
当θ1=20°,θ2=20°,θ4=30°,d3=-100时,SCARA机器人在此状态时,位姿如图所示:
此时,在matlab中用欧拉角公式解位姿坐标,代码及结果如下:
%输入欧拉角度
alpha = input('Roatate around the z-axis in alpha = ');
beta = input('Roatate around the y-axis in alpha = ');
gamma = input('Roatate around the x-axis in alpha = ');
%分别计算出绕X、Y、Z轴的旋转算子
RZ = [cosd(alpha) -sind(alpha) 0
sind(alpha) cosd(alpha) 0
0 0 1];
RY = [cosd(beta) 0 sind(beta)
0 1 0
-sind(beta) 0 cosd(beta)];
RX = [ 1 0 0
0 cosd(gamma) -sind(gamma)
0 sind(gamma) cosd(gamma)];
T =RZ*RY*RX %计算旋转矩阵TAB 此处绕z轴转70°,x轴和y轴均为0°。在命令行输入,即可获得:
并且机器人坐标系{4}相对于坐标系{0}的位姿为:
p1=20;p2=20;p3=0;p4=30; %"p"表示关节角theta
d1=200;d2=30;d3=-100;d4=-100; %“d”为连杆偏距
a0=0;a1=200;a2=200;a3=0; %“a”为连杆长度
A1=[cosd(p1),-sind(p1),0,0;sind(p1),cosd(p1),0,0;0,0,1,d1;0,0,0,1];
A2=[cosd(p2),-sind(p2),0,a1;sind(p2),cosd(p2),0,0;0,0,1,d2;0,0,0,1];
A3=[1,0,0,a2;0,1,0,0;0,0,1,d3;0,0,0,1];
A4=[cosd(p4),-sind(p4),0,0;sind(p4),cosd(p4),0,0;0,0,1,d4;0,0,0,1];
A5=A1*A2*A3*A4;
A5即:当θ1=20°,θ2=20°,θ4=30°,d3=-100时,机器人坐标系{4}相对于坐标系{0}的位姿为:
其中:Px=341.1474 , Py=196.9616 , Pz=30. 与仿真结果一致。
且末端执行坐标系相对于基坐标系的姿态与利用欧拉角公式计算所得结果一致。
ps:此博客为本人在本科机器人方向课堂作业,有出错的地方还请各位大牛指正!