dx12 龙书第五章学习笔记 -- 渲染流水线

1.模型的表示：

实体3D对象是借助三角形网络来近似表示的,这些3D物体可以通过3D建模工具生成。

2.计算机色彩基础：

初学者以RGB值(r,g,b)来描述颜色,每款显示器所能发出的红绿蓝三色光的强度都是有限的。为了描述光的强度,我们常将它量化为范围为0~1归一化区间的值。0表示无强度,1表示强度最大。

颜色计算：

混合两种颜色：

加 减 标量乘法 -- 适合 

显然点积和叉积就不适合颜色向量了

颜色向量专属的颜色运算,分量式乘法：

 这种运算主要运用于光照方程。如果有颜色(r, g,b)的入射光,照射到一个反射50%红色光、75%绿色光、25%蓝色光且吸收剩余光的表面：

由于颜色相加操作时,分量可能会超出1或者低于0,比如1.1我们看作和1强度一致,然后钳制到0~1的范围(1.1->1,-0.5->0)

alpha分量：

不透明度,在混合(blending)技术中起到了至关重要的作用,暂时设置为1

：XMVECTOR

DirectXMath提供颜色的分量式乘法计算函数：

// 返回c1⊗c2
XMVECTOR XM_CALLCONV XMColorModulate(
    FXMVECTOR C1,
    FXMVECTOR C2
);

128位颜色：每个分量使用浮点值

32位颜色：每个分量使用0~255(8个字节)

DirectX::PackedVector命名空间提供以下结构用于存储32位颜色：

struct XMCOLOR {
  union {
    struct {
      uint8_t b; // 8个字节 -- 所以cout是以char形式展示
      uint8_t g;
      uint8_t r;
      uint8_t a;
    };
    uint32_t c;
  };

  void      XMCOLOR();
  void      XMCOLOR(
    const XMCOLOR & unnamedParam1
  );
  XMCOLOR & operator=(
    const XMCOLOR & unnamedParam1
  );
  void      XMCOLOR(
    XMCOLOR && unnamedParam1
  );
  XMCOLOR & operator=(
    XMCOLOR && unnamedParam1
  );
  void      XMCOLOR(
    uint32_t Color
  ) noexcept;
  void      XMCOLOR(
    float _r,
    float _g,
    float _b,
    float _a
  ) noexcept;
  void      XMCOLOR(
    const float *pArray
  ) noexcept;
  void      operator uint32_t() noexcept;
  XMCOLOR & operator=(
    const uint32_t Color
  ) noexcept;
};

可以看到union中,4个8位整数,封装成一个32位整数值。由于这种封装关系,因此在32位颜色与128位颜色的互相转换不单纯的是乘上或除以255,还需要一些额外的位运算。

对此,DirectXMath库提供了获取XMCOLOR类型实例并返回相应XMVECTOR类型值的函数：

XMVECTOR XM_CALLCONV PackedVector::XMLoadColor(
    const XMCOLOR* pSource
);

XMCOLOR类中使用的格式为ARGB而不是RGBA？？

XMVECTOR转换到XMCOLOR的函数：

void XM_CALLCONV PackedVector::XMStoreColor(
    XMCOLOR* pDestination,
    FXMVECTOR V
);

128位颜色值常用于高精度的颜色计算,但最终存储在后台缓冲区中的像素颜色数据,却往往是以32位颜色值来表示。目前的物理显示设备不足以充分发挥出更高色彩分辨率的优势

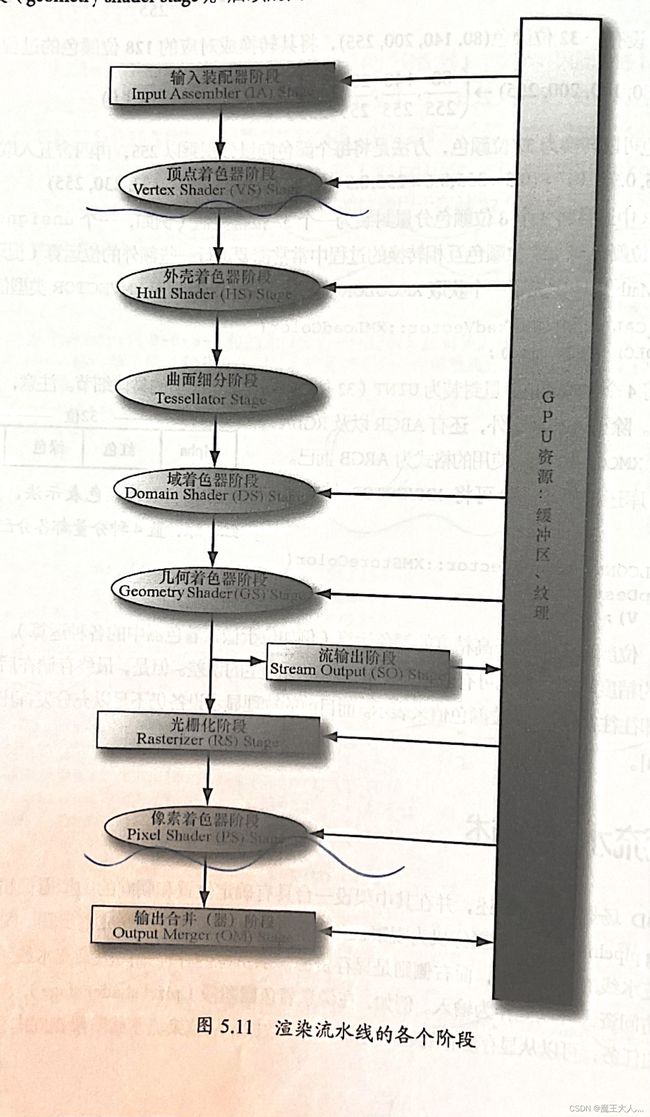
3.渲染流水线：

渲染流水线 rendering pipeline是以摄像机为观察视角而生成2D图像的一系列完整步骤

输入装配器阶段->顶点着色器阶段->外壳着色器阶段->曲面细分阶段->域着色器阶段->几何着色器阶段(->流输出阶段)->光栅化阶段->像素着色器阶段->输出合并(器)阶段

GPU资源:缓冲区、纹理

图中典型的箭头的意义：①GPU资源->输入装配器阶段：可以访问GPU资源并完成输入②输出合并器阶段->GPU资源:把数据写入后台缓冲区和深度模板缓冲区这样的纹理当中

①输入装配器阶段：

从显存中读取几何数据(顶点和索引),再将他们装配为几何图元

顶点：一种特殊点,其意义不止于此,为顶点添加法向量、纹理坐标等

D3D为用户自定义顶点格式提供了很高的灵活性

图元拓扑：primitive topology

void ID3D12GraphicsCommandList::IASetPrimitiveTopology(
  D3D_PRIMITIVE_TOPOLOGY PrimitiveTopology);

typedef enum D3D_PRIMITIVE_TOPOLOGY
{
  D3D_PRIMITIVE_TOPOLOGY_UNDEFINED = 0,
  D3D_PRIMITIVE_TOPOLOGY_POINTLIST = 1,
  D3D_PRIMITIVE_TOPOLOGY_LINELIST = 2,
  D3D_PRIMITIVE_TOPOLOGY_LINESTRIP = 3,
  D3D_PRIMITIVE_TOPOLOGY_TRIANGLELIST = 4,
  D3D_PRIMITIVE_TOPOLOGY_TRIANGLESTRIP = 5,
  D3D_PRIMITIVE_TOPOLOGY_LINELIST_ADJ = 10,
  D3D_PRIMITIVE_TOPOLOGY_LINESTRIP_ADJ = 11,
  D3D_PRIMITIVE_TOPOLOGY_TRIANGLELIST_ADJ = 12,
  D3D_PRIMITIVE_TOPOLOGY_TRIANGLESTRIP_ADJ = 13,
  D3D_PRIMITIVE_TOPOLOGY_1_CONTROL_POINT_PATCHLIST = 33,
  D3D_PRIMITIVE_TOPOLOGY_2_CONTROL_POINT_PATCHLIST = 34,
   ┆
  D3D_PRIMITIVE_TOPOLOGY_32_CONTROL_POINT_PATCHLIST = 64,
} D3D_PRIMITIVE_TOPOLOGY;

通过命令列表修改图元拓扑,所有的绘制调用会沿用当前设置的图元拓扑方式,直到改变

mCommandList->IASetPrimitiveTopology(D3D_PRIMITIVE_TOPOLOGY_TRIANGLELIST); // 三角形列表

 图元拓扑类型请自行翻书(P148~150)查阅,最常使用的图元拓扑类型是三角形列表D3D_PRIMITIVE_TOPOLOGY_TRIANGLELIST

索引：

Vertex quad[6] = {
    v0, v1, v2, // 三角形0
    v0, v2, v3, // 三角形1
};

为三角形指定顶点顺序是一项十分重要的工作,我们称这个顺序为绕序

⭐绕序会遇到问题：DX12默认背面剔除,绕序决定了三角形的法线朝向,后续讨论

创建一个顶点列表和索引列表,在顶点列表中收录一份所有独立的顶点,并在索引列表中存储顶点列表的索引值

每个图形适配器具有特定大小的缓存,刚处理过的顶点数据可以被临时存储在缓存中,所以设计索引顺序时,优先引用需要复用的顶点,就能快速引用

②顶点着色器阶段：Vertex Shader stage (VS)

输入和输出都是单个顶点的函数,每个要被绘制的顶点都经过顶点着色器的处理再送往后续阶段

// 我们可以认为硬件中执行的是下列过程
for(UINT i = 0; i < numVertices; ++i)
    outputVertex[i] = VertexShader( inputVertex[i]; )

这一阶段操作由GPU执行,运行速度极快。可以用VS来实现许多特效,比如变换、光照和位移贴图

在VS阶段,不但可以访问输入的顶点数据,还可以访问GPU资源(纹理等)

局部空间和世界空间:

世界空间：全局场景坐标系 world space

局部空间：局部坐标系 local space -- 通常以目标物体的中心为原点

3D美工在局部空间中绘制3D模型,再将其转换到世界空间中

世界变换(world transform):局部空间->世界空间 -- 使用的变换矩阵为：世界矩阵

当我们需要在场景中多次绘制同一个物体,我们保存一个顶点和索引数据的局部空间副本,然后按所需次数绘制此图形,辅以不同的世界矩阵来指定物体在世界空间中的位置、方向、大小 -- 这种方法叫实例化

构建世界矩阵的方法：(在第3章笔记中较为详细的讨论过了)

其中每一行分别存储的是局部空间的x轴、y轴、z轴和原点相对于全局空间的齐次坐标

我们也可以将世界矩阵视作一系列变换组合W,其中,分别是缩放矩阵、旋转矩阵和平移矩阵

假设我们在局部空间定义了一个单位正方形,其最小点和最大点的坐标分别为(-0.5,0,-0.5)与(0.5,0,0.5)。现要求出一个世界矩阵,使正方形在世界空间中的边长为2,并在世界空间xz平面内顺时针旋转45°,且中心位于世界空间坐标(10,0,10)处。据此我们构造S/R/T矩阵,并求得世界矩阵W：

  

​​​​⭐这种方法比考虑Qw,Uw,Vw,Ww求取世界矩阵的方法简单的多,只需要了解物体在世界空间中的大小、朝向和位置即可

思考,假设两种情况：

①局部坐标系原点在(0,0,0)处,且坐标轴与世界坐标轴平行；

②也是局部坐标轴原点在(10,0,10)处,但局部x轴y轴z轴相对于世界坐标轴的坐标为   就是W的前3行分量；

对于①而言,在局部坐标系中的物体通过SRT变换到世界空间,那么得到的最终物体是一个倾斜45°的正方形且平移到(10,0,10);

对于②而言,从世界空间观察局部空间,正方形已经在最终位置,只是将其局部坐标通过QUVW的分量构造的世界矩阵转换为世界坐标,物体并没有移动

所以这两种方式是等价的,最终物体都在目标位置

这里有点绕,不知道自己有没有想或写清楚,反正我们假设在原点建模(局部坐标系),然后通过SRT矩阵转换到特定位置即可

观察空间：

摄像机空间,在此局部空间中,虚拟摄像机位于原点,沿z轴的正方向观察,x轴指向摄像机的右侧,y轴指向摄像机的上方

由世界空间到观察空间的坐标变换叫做视图变换(view transform),变换矩阵叫做观察(视图)矩阵view matrix

⭐回归：两个坐标系之间的变换,假设坐标系A的x、y、z轴及其原点相对于坐标轴B的齐次坐标为u,v,w,Q,那么从坐标系A转换到坐标系B的坐标转换矩阵为:,则坐标系B到坐标系A的变换矩阵为W矩阵的逆,uvw部分3x3做转置,Q部分1×3取反

从世界空间转换到观测空间,可以通过观测空间的坐标轴相对于世界空间来构造,但DirectXMath库为我们提供了计算观察矩阵的函数：

XMMATRIX XM_CALLCONV XMMatrixLookAtLH(
    FXMVECTOR EyePosition, // 虚拟摄像机位置Q
    FXMVECTOR FocusPosition, // 摄像机观测点 -- 用于计算摄像机正前方向量
    FXMVECTOR UpDirection // 一般是(0,0,1,0) 摄像头向上方向
);

使用示例：

XMVECTOR pos = XMVectorSet(5, 3, -10, 1.f);
XMVECTOR target = XMVectorZero();
XMVECTOR up = XMVectorSet(0.f, 1.f, 0.f, 0.f);

XMMATRIX v = XMMatrixLookAtLH(pos, target, up);

投影和齐次裁剪空间： 

摄像机有一个关键组成要素：摄像机可观察到的空间体积(volumn of space),此范围可以由一个四棱锥截取的平截头体(frustum,四棱台)来表示

 下一个任务是,将四棱台内的3D几何体投影到一个2D投影窗口之中

我们将由顶点到观察点的连线称为顶点的投影线,将3D顶点v变换至其投影线与2D投影平面交点v'的透视投影变换

 在观察空间中,我们可以通过近平面n,远平面f,垂直视场角α以及纵横比r这四个参数来定义一个：以原点作为投影的中心,并沿z轴正方向进行观察的平截头体

注意,近平面和远平面都平行于xy平面,所以能方便确定它们沿着z轴到原点的距离

纵横比(长宽比) Aspect Ratio  投影窗口的宽度除以高度

因为投影窗口实质上即为观察空间中场景的2D图像,由于该图像被映射到后台缓冲区中,所以我们希望投影窗口和后台缓冲区两者的纵横比保持一致

接下来利用相似三角形的性质来求取平截头体中的点投影到投影窗口内的位置

注意：投影窗口具体大小以及离摄像机多远是不重要的,因为其本身就是通过比率从视锥体投影到投影平面上,然后又会按比率缩放到屏幕上。我们只需要确定垂直视场角FovY以及宽高比r=AspectRatio。现在我们只需假设一个具体的值(比如高度),那么其他长度就可以表示出来。比如：假设高度为2,那么宽为2r,投影窗口到摄像机的距离为。在这种假设情况下：

这里遇到的问题,硬件会涉及一些改变投影窗口(后台缓冲区)大小有关的操作,所以纵横比可能改变,如果我们能去除投影窗口对纵横比的依赖,那么处理过程会更简单 -- 我们的解决办法：将x坐标上的投影区间从[-r,r]缩放到归一化区间[-1,1] -- x和y坐标就成为了规格化设备坐标(Normalized Device Coordinates,NDC) -- 注意这里没有对z坐标进行归一化处理

现在我们希望求出顶点(x,y,z)在投影平面z=d的投影(x',y',d),其中顶点是视锥体里的任意点。

因为：

所以：

假设原投影窗口的高为h,宽为2：(x是在平截头体中的坐标 x'是投影在z=d的投影平面的坐标)

经过归一化处理后：

因此：在NDC坐标中,投影窗口的高和宽都为2,所以它的大小是固定的,硬件无须知道纵横比。

但是我们一定要将投影坐标映射到NDC空间中,因为图形硬件会假设我们完成此项工作

我们尝试用矩阵来表示这种投影变换,但因为NDC下xy坐标的公式中存在z,也就是说不是线性关系,所以构造矩阵时分别处理非线性变换(除以z)和线性变换

我们构造矩阵：

这里令元素P[2][3]=1 P[3][3]=0来实现

⭐我们设置了常量AB,利用它们来把输入的z坐标变换到归一化范围内 -- 

因为我们需要执行非线性部分除以z的操作,但此时没有最初的z坐标可用,所以我们将输入的z坐标输出到w位置

我们得到：

再根据我们保存在w处的z值,对该坐标每个分量除以这个z值：

⭐归一化深度值的作用：

因为所有的投影点都会位于2D投影空间中,所以我们看似可以丢弃原始的3D z坐标了。然而为了实现深度缓冲算法,我们仍然需要保留这些3D深度信息。

深度坐标也需要被映射到[0,1]以内

我们构建一个保序函数g(z),将z坐标从[n,f]映射到[0,1]中

我们看到Projection矩阵中：,我们据此构造保序函数

我们根据下列约束求出对应的A和B：①条件1：g(n)=A+B/n=0 将近平面映射为0 ②条件2：g(f)=A+B/f=1 将远平面映射为1

得到： 因此我们构造出一个函数g(z),观察其图像可以看出其非线性的保序函数

所以实则没有“投影”z,因为投影面已经固定了投影后z坐标。此矩阵只是在投影并归一化xy坐标的基础上,顺带归一化原z坐标,以便深度缓冲使用

-- 这里的理解可以结合games101一起理解

所以,我们得到了透视投影矩阵perspective projection matrix：

其中 r：横纵比,α：垂直视场角,n：近平面,f：远平面

当然,坐标乘上投影矩阵后,坐标处于齐次裁剪空间或投影空间中,还需要完成透视除法,使用NDC(规格化设备坐标)来表示几何体

DirectXMath提供构造透视投影矩阵的函数：

XMMATRIX XM_CALLCONV XMMatrixPerspectiveForLH(
    float FovAngleY, // 弧度制表示的垂直视场角r
    float Aspect, // 纵横比=宽度/高度
    float NearZ, // 原点到近平面的距离
    float FarZ // 原点到远平面的距离
);

// Aspect:
需要与后台缓冲区的纵横比一致 = mClientWidth/mClientHeight

③曲面细分阶段：

曲面细分阶段：利用镶嵌化处理技术对网格中的三角形进行细分(subdivide),以此来增加物体表面的三角形数量,再将这些新增的三角形偏移到适当的位置,使网格表现出更加细腻的细节

有点：①我们借此实现一种细节层次机制,对离摄像机近的三角形进行镶嵌化处理,而对远的三角形不做任何更改②内存中仅维护简单的低模,为它动态地增添额外的三角形,节省内存资源③处理动画和物理模拟时使用低模,在渲染过程中经镶嵌化处理高模网络        

曲面细分是Direct3D 11中新引入的处理阶段,它们为我们提供了一种利用GPU即可对几何体进行镶嵌化处理的手段 -- 之前只能在CPU上实现镶嵌化处理 

曲面细分是一个可选的渲染阶段 -- 第十四章讨论

④几何着色器阶段：Geometry Shader stage(GS)

几何着色器是一个可选的渲染阶段 -- 第十二章讨论

几何着色器接收的输入应当是完整的图元,比如图元拓扑是三角形列表,则传入的是定义三角形的三个顶点 -- 几何着色器的优点是可以创建或销毁几何体(比如创建新的顶点)

几何着色器常用作：将一个点或一条线扩展为一个四边形

注意：渲染流水线中“流输出”阶段的箭头。几何着色器可以将顶点数据流输出至显存中的某个缓冲区内

⑤裁剪：

这里的裁剪指的是将跨越平截头体(可观察的视觉范围)边界线的几何体进行裁剪操作,保留平截头体以内的部分

裁剪操作由硬件执行,我们不展示过多的细节。作为了解,推荐一种比较流行的裁剪算法--苏泽兰(萨瑟兰德)-霍奇曼裁剪算法 -- 总的来说,算法的整体思路是找到平面与多边形的所有交点,将这些顶点按顺序组织成新的裁剪多边形

⑥光栅化阶段：

计算出屏幕上对应像素点的像素颜色

我们通过视口变换,已经将3D空间中坐标转换到2D的NDC空间中

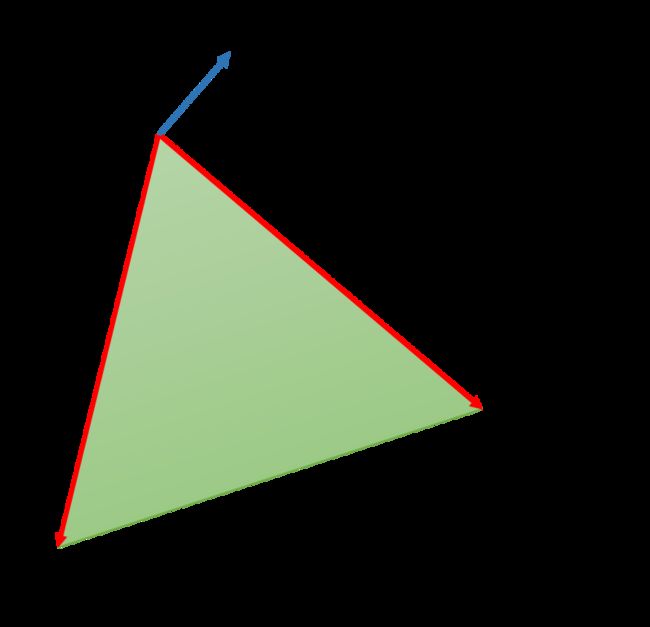
⭐背面剔除：

每个三角形都有两个面,在默认情况下我们采用以下约定对它们进行区分：-- 我们可以修改这个默认情况

如果组成三角形的顶点顺序为v0, v1, v2,那么我们通过下述方法来计算三角形的法线n:

我们通过公式可以看出,如果三角形三个顶点的绕序为顺时针,则其正面竖直朝上(面向我们)

 法向量从正面射出,另一面是背面。如果观察者看到的是三角形的正面,则称此三角形为正面朝向。

背面剔除：将背面朝向的三角形从渲染流水线中去除。因为对于一个实体物体,正面朝向的三角形会挡住背面朝向的三角形。

顶点属性插值：

我们为顶点附加颜色、法向量和纹理坐标等属性,经过视口变换后,我们需要为求取三角形内诸像素所附的属性而进行插值(interpolate),除了上述顶点属性外,还需要对顶点的深度值进行插值

为了得到屏幕空间中各个顶点的插值属性,我们往往需要通过一种名为透视矫正插值的方法,对3D空间中三角形的属性进行线性插值。

-- 从本质上来讲,插值法即利用三角形顶点的属性值计算出其内部像素的属性值。

 我们无需了解透视矫正插值法的具体数学细节,硬件会自动完成相应的处理

通过下图可以看出,从3D线段投影到投影窗口成为2D线段的过程,是非线性插值

⑦像素着色器阶段：pixel shader(PS) 

GPU执行的阶段,针对每个像素片段(pixel fragment)进行处理,并根据顶点的插值属性作为输入来计算出对应的像素颜色。

像素着色器既可以直接返回一种单一的恒定颜色,也可以实现逐像素光照、反射、阴影等复杂效果

⑧输出合并阶段：

通过像素着色器生成的像素片段会被送入输出合并阶段,在这个阶段,一些像素片段可能会被丢弃(例如没通过深度测试或模板测试的像素片段) -- blend混合操作也是在这个阶段实现的(对后台缓冲区的对应像素融合而不是覆写) 一些透视效果是通过混合技术实现的 -- 第10章详细讲解

---

⭐索引缓冲区的使用以及不使用：

①不使用索引缓冲区：

绘制函数：DrawInstanced()

void DrawInstanced(
  UINT VertexCountPerInstance, // 实例要绘制的顶点数
  UINT InstanceCount, // 实例数 -- 未开启实例化:1
  UINT StartVertexLocation, // 顶点缓冲区读取的第一个顶点的位置
  UINT StartInstanceLocation // 从顶点缓冲区读取每个实例数据之前添加到每个索引的值 -- 未开启实例化:0
);

②使用索引缓冲区：

使用索引缓冲区的目的是,防止重复保存同一个Vertex结构,以免浪费空间,用索引代替了之前Vertex的排排坐

绘制函数：DrawIndexedInstanced()

void DrawIndexedInstanced(
  UINT IndexCountPerInstance, // 从每个实例的索引缓冲区读取的索引数 -- 不开启实例化:就是总索引个数
  UINT InstanceCount, // 实例数:1
  UINT StartIndexLocation, // 从索引缓冲区读取的第一个索引位置
  INT  BaseVertexLocation, // 从顶点缓冲区读取顶点之前添加到每个索引的值
  UINT StartInstanceLocation // 从顶点缓冲区读取每个实例数据之前添加到每个索引的值 -- 不开启实例化:0
);

示例：

mCommandList->IASetVertexBuffers(0, 1, &mBoxGeo->VertexBufferView());
mCommandList->IASetIndexBuffer(&mBoxGeo->IndexBufferView());
mCommandList->IASetPrimitiveTopology(D3D11_PRIMITIVE_TOPOLOGY_TRIANGLELIST);

mCommandList->DrawIndexedInstanced(
	mBoxGeo->DrawArgs["box"].IndexCount, 
	1, 0, 0, 0);

⭐三角形带：D3D_PRIMATIVE_TOPOLOGY_TRIANGLESTRIP：

三角形条带用于绘制这样连续的三角形图形,其中处于中间位置的顶点呗相邻的三角形所共用,具体来说,利用n个顶点即可生成n-2个三角形。

我们可以不使用索引缓冲区,直接利用顶点缓冲区(顺序：01234567),然后直接DrawInstanced()即可绘制三角形带。

注意：按照01234567的顺序明显不符合D3D的绕序规矩。但是其实,GPU内部会对偶数三角形中两个顶点的顺序进行调换(比如123换成132),以保持绕序的一致性。-- DirectX置换的后两个顶点的顺序,OpenGL置换的前两个顶点的顺序。

三角形带状不同于三角形列表,三角形列表是每3个顶点绘制一个三角形,而三角形条带是多个连续顶点(当然大于等于3个),绘制条带。注意如果三角形条带的顶点个数是三个,其实就变成了三角形列表。 -- 后面几何着色器中会涉及相关内容