评估分类模型—混淆矩阵Confusion Matrix与评估指标
对于设计好的分类模型,需要大量的数据集来对其性能进行评估,因此了解评估指标是十分重要的。
一、二分类混淆矩阵 Confusion Matrix
严格来说,对于二分类问题,没有标签,只有正例和反例。二分类问题的混淆矩阵如下:

评估指标计算公式:
- A c c u r a c y = T P + T N T P + T N + F P + F N Accuracy=\frac{TP+TN}{TP+TN+FP+FN} Accuracy=TP+TN+FP+FNTP+TN
- P r e c i s i o n = T P T P + F P Precision=\frac{TP}{TP+FP} Precision=TP+FPTP
- R e c a l l = T P T P + F N Recall=\frac{TP}{TP+FN} Recall=TP+FNTP
- F 1 − S c o r e = 2 1 P r e c i s i o n + 1 R e c a l l = 2 × P r e c i s i o n × R e c a l l P r e c i s i o n + R e c a l l F1-Score=\frac{2}{\frac{1}{Precision} + \frac{1}{Recall}}=\frac{2 \times Precision \times Recall}{Precision + Recall} F1−Score=Precision1+Recall12=Precision+Recall2×Precision×Recall
- s p e c i f i c i t y = T N F P + T N specificity=\frac{TN}{FP+TN} specificity=FP+TNTN
下面以猫狗二分类问题为例,讨论二分类的混淆矩阵及其评估指标:
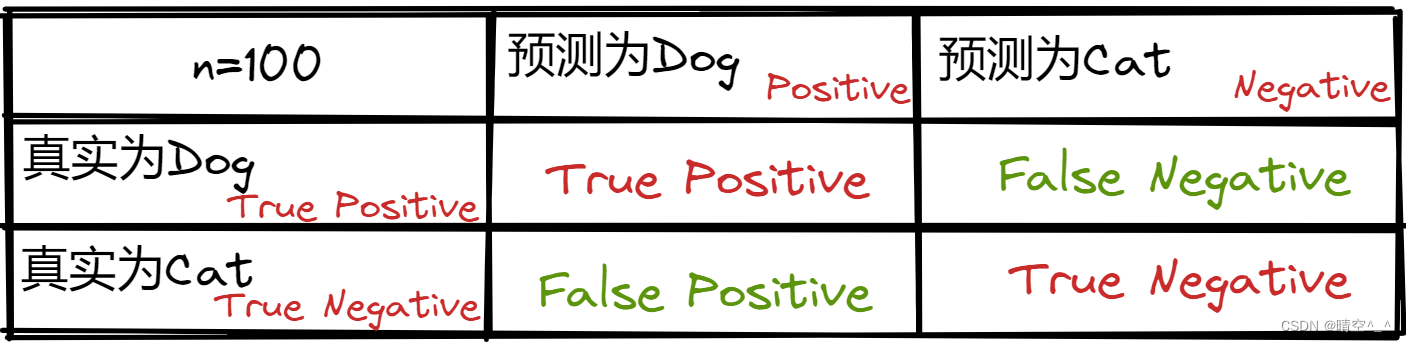
如图,在猫狗分类中中,将Dog作为正例,不是狗(猫)作为反例。上侧为预测值,左侧为真实值。主对角线(红色)为预测正确值,副对角线(绿色)为预测错误值。
其中:
- T P + F P TP+FP TP+FP为数据集中狗的数量
- F P + T N FP+TN FP+TN为数据集中猫的数量
- T P + T N TP+TN TP+TN为模型的正确分类数量
1、正确率
A c c u r a c y = 正确分类个数 所有数据 = T P + T N T P + T N + F + F N Accuracy=\frac{正确分类个数}{所有数据}=\frac{TP+TN}{TP+TN+F{+FN}} Accuracy=所有数据正确分类个数=TP+TN+F+FNTP+TN
即,
A c c u r a c y = 45 + 35 45 + 35 + 5 + 35 = 0.8 Accuracy=\frac{45 + 35}{45 + 35 + 5 + 35} = 0.8 Accuracy=45+35+5+3545+35=0.8
2、查准率
预测为狗的数据中有多少是真正的狗
P r e c i s i o n = T P 预测的狗个数 = T P T P + F P Precision=\frac{TP}{预测的狗个数}=\frac{TP}{TP+FP} Precision=预测的狗个数TP=TP+FPTP
即,
p r e c i s i o n = 45 45 + 15 = 0.75 precision=\frac{45}{45 + 15} = 0.75 precision=45+1545=0.75
3、召回率、查全率、敏感性
真实是狗的数据中有多少被检测出来
R e c a l l = T P 真实的狗的个数 = T P T P + F N Recall=\frac{TP}{真实的狗的个数}=\frac{TP}{TP+FN} Recall=真实的狗的个数TP=TP+FNTP
即,
R e c a l l = 45 45 + 5 = 0.9 Recall=\frac{45}{45 + 5} = 0.9 Recall=45+545=0.9
4、F1 Score
F1 Score是Precision和Recall的调和平均数,综合反映分类器的Precision和Recall。即,单独 P r e c i s i n o Precisino Precisino或 R e c a l l Recall Recall有一个高,F1-Score都不会高。(可以类比于两个电阻并联,一个电阻高、一个电阻低,结果还是低)
F 1 − S c o r e = 2 1 P r e c i s i o n + 1 R e c a l l = 2 × P r e c i s i o n × R e c a l l P r e c i s i o n + R e c a l l F1-Score=\frac{2}{\frac{1}{Precision} + \frac{1}{Recall}}=\frac{2 \times Precision \times Recall}{Precision + Recall} F1−Score=Precision1+Recall12=Precision+Recall2×Precision×Recall
即,
F 1 − S c o r e = 2 × 0.75 × 0.9 0.75 + 0.9 = 0.82 F1-Score=\frac{2 \times 0.75 \times 0.9}{0.75 + 0.9}=0.82 F1−Score=0.75+0.92×0.75×0.9=0.82
5、特异性
真实为猫(负例)中有多少被选中
s p e c i f i c i t y = T N 真实为猫的数量 = T N F P + T N specificity=\frac{TN}{真实为猫的数量}=\frac{TN}{FP+TN} specificity=真实为猫的数量TN=FP+TNTN
即,
s p e c i f i c i t y = 35 15 + 35 = 0.7 specificity=\frac{35}{15 + 35} = 0.7 specificity=15+3535=0.7
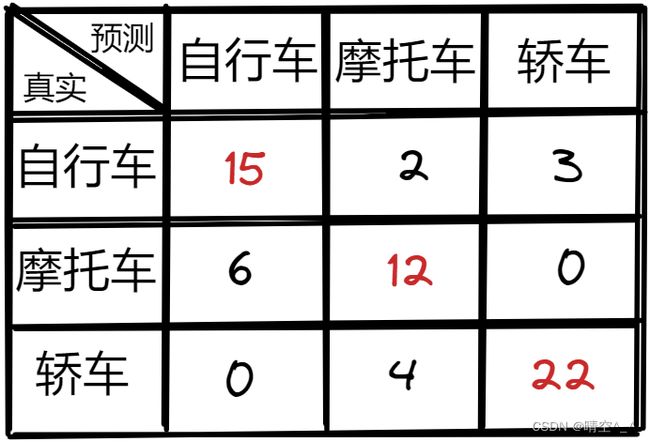
二、多分类混淆矩阵 Multiclass Classifiers
多分类混淆矩阵与二分类十分相似,只是在计算precision、recall等时需要针对每个类单独计算。
例如:
-
A c c u r a c y = 15 + 12 + 22 15 + 2 + 3 + 6 + 12 + 4 + 22 = 0.7656 Accuracy=\frac{15+12+22}{15+2+3+6+12+4+22}=0.7656 Accuracy=15+2+3+6+12+4+2215+12+22=0.7656
-
自行车: P r e c i s i o n = 15 15 + 6 = 0.71 Precision=\frac{15}{15 + 6}=0.71 Precision=15+615=0.71, R e a c a l l = 15 15 + 2 + 3 = 0.75 Reacall=\frac{15}{15 + 2 + 3}=0.75 Reacall=15+2+315=0.75
-
摩托车: P r e c i s i o n = 12 2 + 12 + 4 = 0.66 Precision=\frac{12}{2 + 12 + 4}=0.66 Precision=2+12+412=0.66, R e a c a l l = 12 12 + 6 = 0.66 Reacall=\frac{12}{12 + 6}=0.66 Reacall=12+612=0.66
-
轿车: P r e c i s i o n = 22 22 + 3 = 0.88 Precision=\frac{22}{22 + 3}=0.88 Precision=22+322=0.88, R e a c a l l = 22 22 + 4 = 0.85 Reacall=\frac{22}{22 + 4}=0.85 Reacall=22+422=0.85
-
平均: P r e c i s i o n = 0.71 + 0.66 + 0.88 3 = 0.75 Precision=\frac{0.71+0.66+0.88}{3}=0.75 Precision=30.71+0.66+0.88=0.75, R e c a l l = 0.75 + 0.66 + 0.85 3 = 0.75 Recall=\frac{0.75+0.66+0.85}{3}=0.75 Recall=30.75+0.66+0.85=0.75
-
F1 Score: F 1 − S c o r e = 2 × P r e c i s o n × R e c a l l P r e c i s i o n × R e c a l l = 2 × 0.75 × 0.75 0.75 + 0.75 = 0.75 F1-Score=\frac{2 \times Precison \times Recall}{Precision \times Recall} = \frac{2 \times 0.75 \times 0.75}{0.75 + 0.75}=0.75 F1−Score=Precision×Recall2×Precison×Recall=0.75+0.752×0.75×0.75=0.75
多分类F1 Score时每一类F1 Score的平均值。
在多分类混淆矩阵中,热力图的形式较为常见,如图:
三、ROC曲线(受试者工作特征曲线)Receiver Operating Characteristic Curve
FPR(伪正类率): F P R = F P F P + T N FPR=\frac{FP}{FP+TN} FPR=FP+TNFP,即负类数据被分成正类的比例
TPR(真正类率): T P R = T P T P + F N TPR=\frac{TP}{TP+FN} TPR=TP+FNTP,即正类数据中被分成正类的比例
1、ROC曲线直观理解
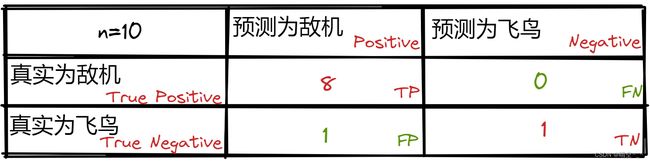
ROC曲线起源于二战时期雷达兵对雷达信号的判断。雷达兵的任务是解析雷达信号,但雷达信号含有噪声(如一只大鸟),所以每当雷达屏幕出现信号时,雷达兵就需对其进行判断。有的雷达兵比较谨慎(阈值低),所有信号都判断为敌机;有的士兵比较乐观(阈值高),所有信号都判断为大鸟。一下是一位雷达兵一天的判断结果:
此时:
- T P R = T P T P + F N = 1 TPR=\frac{TP}{TP + FN} = 1 TPR=TP+FNTP=1
- F P R = F P F P + T N = 0.5 FPR=\frac{FP}{FP+TN}=0.5 FPR=FP+TNFP=0.5
对于系统来说,我们希望TPR越高越好,因为这样可以把所有的敌机都检测出来。同时,我们希望FPR越低越好,因为这样可以减少误判,即理想情况下, T P R = 1 TPR=1 TPR=1、 F P R = 0 FPR=0 FPR=0。但是,对一般的系统而言,两者不可兼得:如果降低士兵的阈值,那么理想情况下敌机都会被判断出来,但是有些飞鸟不可避免的也会被判断为敌机,这会导致 T P R TPR TPR高的同时 F P R FPR FPR也高;相对应的,若提高士兵的阈值,那么理想情况下所有的飞鸟都不会被判断为敌机,但是有些敌机不可避免的被判断为飞鸟(这会对己方士兵造成巨大伤害),这会导致 F P R FPR FPR低的同时 T P R TPR TPR也低。因此,一般情况下,ROC曲线是一个正比例递增函数,且在 y = x y=x y=x曲线的上方。
2、ROC曲线绘制原理



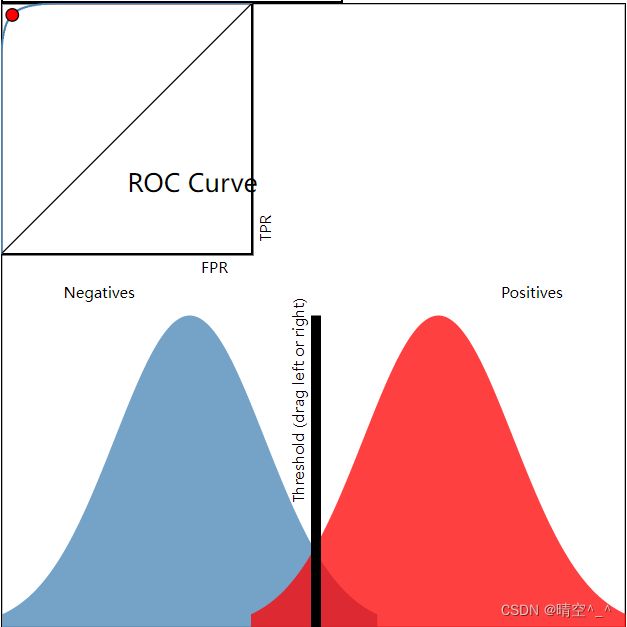
本图在http://www.navan.name/roc/中绘制,可以实时动态交互。读者可以边看边更改ROC曲线设置加深理解。
在上图中,蓝色曲线表示负例,红色表示正例,黑粗色竖线表示阈值。
左上与右上是站在士兵(阈值)的角度,此时,雷达(分类器)的性能是确定的。即,ROC曲线是确定的,改变阈值只是改变ROC曲线上的红色坐标点。
如左上图:若阈值选的过低,则正例全被判断为正例( T P R = 1 TPR=1 TPR=1),但是负例也有大部分被判断为正例( F P R FPR FPR接近1),此时ROC曲线中的坐标点在右上角。
如右上图:若阈值选的过高,则负例全被判断为负例( F P R = 0 FPR=0 FPR=0),但正例也有大部分被判断为负例( T P R TPR TPR接近0),此时ROC曲线中的坐标点在左下角。
若阈值选在正例与负例的中间位置,那么 T P R TPR TPR值比较高, F P R FPR FPR值比较低,是一个比较理想的状态。
左下与右下是站在雷达(分类器)的角度。
如左下图:若分类器性能不足,则正例与负例就是相互包含,这时ROC曲线就趋近于 y = x y=x y=x函数(即FPR增加多少,TPR减少多少)。
如右下图,若分类器性能很好,则正例和负例就会”分“的很开,这时ROC曲线就越趋近于一个直角。理想情况下是正例与负例完全分开,若阈值选取恰当,就会实现 T P R = 1 TPR=1 TPR=1、 F P R = 0 FPR=0 FPR=0,就是ROC曲线矩形的左上角。
3、AUC曲线
AUC,(Area Under Curve),ROC曲线下的面积,显然这个面积小于1,又因为ROC曲线一般都处于y=x这条直线的上方,所以AUC一般在0.5到1之间。AUC值相较于ROC曲线可以更好的量化分类器的性能。
AUC的含义为,当随机挑选一个正样本和一个负样本,根据当前的分类器计算得到的score将这个正样本排在负样本前面的概率。
从AUC判断分类器(预测模型)优劣的标准:
- AUC = 1,是完美分类器,采用这个预测模型时,存在至少一个阈值能得出完美预测。绝大多数预测的场合,不存在完美分类器。
- 0.5 < AUC < 1,优于随机猜测。这个分类器(模型)妥善设定阈值的话,能有预测价值。
- AUC = 0.5,跟随机猜测一样(例:丢铜板),模型没有预测价值。
- AUC < 0.5,比随机猜测还差;但只要总是反预测而行,就优于随机猜测。
4、ROC曲线优点
ROC曲线可以很好的应对正负样本失衡的情况。
ROC曲线有个很好的特性:当测试集中的正负样本的分布变化的时候,ROC曲线能够保持不变。在实际的数据集中经常会出现类不平衡(class imbalance)现象,即负样本比正样本多很多(或者相反),而且测试数据中的正负样本的分布也可能随着时间变化。
这是因为,在ROC曲线的计算公式中, T P R TPR TPR只针对正例计算, F P R FPR FPR只针对负例计算。因此,即使正负样本比例失衡或者正负样本的比例随时间变化,ROC曲线也不会发生较大变化。
而 A c c u r a c y Accuracy Accuracy、 R e c a l l Recall Recall、 P r e c i s i o n Precision Precision计算公式中需要同时考虑正例、负例,当正例负例比例变化时,其数值会受到较大的影响。
四、正负样本失衡时的分类指标
1、正负样本均衡数据集
| S.NO. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 真实标签 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 预测—模型1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.6 | 0.6 | 0.5 | 0.5 | 0.9 | 0.9 | 0.9 | 0.9 | 0.9 |
| 预测—模型2 | 0.6 | 0.6 | 0.6 | 0.6 | 0.6 | 0.6 | 0.6 | 0.6 | 0.7 | 0.7 | 0.7 | 0.7 | 0.8 | 0.8 | 0.8 |
| F1 阈值=0.5 | F1最好情况 | ROC-AUC | LogLoss | |
|---|---|---|---|---|
| 模型1 | 0.88 | 0.88 | 0.94 | 0.28 |
| 模型2 | 0.67 | 1 | 1 | 0.6 |
从交叉熵损失来说M1的效果远好于M2,虽然M2可以很好的对数据进行分类,但是0.6与0的差距还是有点大,这也是为什么在分类问题中常用softmax而不用回归的原因。
2、负样本远多于正样本
| S.NO. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 真实标签 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 预测—模型1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.9 |
| 预测—模型2 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.9 | 0.9 | 0.9 |
| F1 阈值=0.5 | ROC-AUC | LogLoss | |
|---|---|---|---|
| 模型1 | 0.88 | 0.83 | 0.24 |
| 模型2 | 0.96 | 0.96 | 0.24 |
在本数据集中,模型1将样例14分类为负例FN,模型2将样例13分类为正例FP。对于正样本数量少的情况,我们希望将所有正样本都检测出来(模型2),而不是”随大流“(模型1),因此模型2相比于模型1效果要好,这点在F1-Score和ROC-AUC都可以体现出来。
3、正样本数量远多于负样本
| S.NO. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 真实标签 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 预测—模型1 | 0.1 | 0.1 | 0.9 | 0.9 | 0.9 | 0.9 | 0.9 | 0.9 | 0.9 | 0.9 | 0.9 | 0.9 | 0.9 | 0.9 | 0.9 |
| 预测—模型2 | 0.1 | 0.1 | 0.1 | 0.1 | 0.9 | 0.9 | 0.9 | 0.9 | 0.9 | 0.9 | 0.9 | 0.9 | 0.9 | 0.9 | 0.9 |
| F1 阈值=0.5 | ROC-AUC | LogLoss | |
|---|---|---|---|
| 模型1 | 0.963 | 0.83 | 0.24 |
| 模型2 | 0.96 | 0.96 | 0.24 |
对于正样本数量远多于负样本的情况下,我们希望尽可能的将负样本检测出来。这时,ROC-AUC比较适用。
4、总结
- 对数损失不适用于样本不均衡时的分类评估指标
- ROC-AUC可作为样本正负不均衡时的分类评估指标
- 如果想让少数情况被正确预测,可以选择ROC-AUC作为评估指标