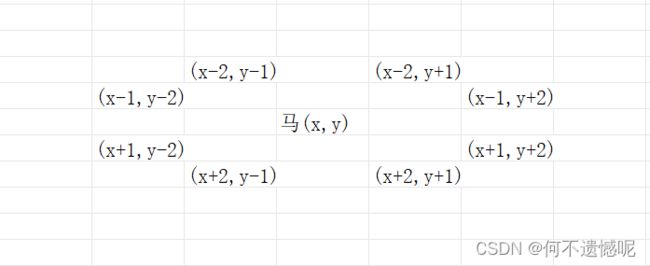bfs算法的介绍,利用bfs解决洛谷问题马的遍历、Meteor Shower S和Corn Maze S。
一.bfs算法的介绍
广度优先搜索,其英语翻译为Breadth-First-Search,所以简称为bfs算法。
可以将bfs算法的实现想象成将一杯水倒在空地上,然后水向四周流散的情况,bfs算法也是一样,问题起点就是水倒在空地上的位置,地图上标记的障碍物就相当于是空地上的障碍,当水流到目标的位置就完成了任务。
下面是用代码运行结果表示的bfs算法遍历情况
初始的二维数组。
0 0 0 0 0
0 0 0 1 0
0 1 0 0 0
0 0 0 1 0
1 0 0 0 0下面是bfs算法的遍历每种情况,没遍历的地方为0,障碍物为1,遍历过的位置为2。
从(0,0)点出发,目标点是(4,4)
2 0 0 0 0
0 0 0 1 0
0 1 0 0 0
0 0 0 1 0
1 0 0 0 02 2 0 0 0
2 0 0 1 0
0 1 0 0 0
0 0 0 1 0
1 0 0 0 02 2 2 0 0
2 2 0 1 0
2 1 0 0 0
0 0 0 1 0
1 0 0 0 02 2 2 2 0
2 2 2 1 0
2 1 0 0 0
2 0 0 1 0
1 0 0 0 02 2 2 2 2
2 2 2 1 0
2 1 2 0 0
2 2 0 1 0
1 0 0 0 02 2 2 2 2
2 2 2 1 2
2 1 2 2 0
2 2 2 1 0
1 2 0 0 02 2 2 2 2
2 2 2 1 2
2 1 2 2 2
2 2 2 1 0
1 2 2 0 02 2 2 2 2
2 2 2 1 2
2 1 2 2 2
2 2 2 1 2
1 2 2 2 02 2 2 2 2
2 2 2 1 2
2 1 2 2 2
2 2 2 1 2
1 2 2 2 2对于范围较大的数据,一般不建议用bfs算法,因为bfs的空间复杂度较大,但是相比于dfs算法,bfs算法的速度更快,对于这两种算法还是得看实际情况分析,用什么算法效率更高。
bfs算法通常依靠队列来实现,可以使用c++库里的queue函数来实现
下面是bfs算法是实现模板
queueq;//设置队列,为结构体类型
point k;
k.x=startx;//startx,starty为起点位置
k.y=starty;
q.push(k);//入队首元素位置
while(!q.empty()){//当队列不为空则,继续遍历
point b=q.front();//取出队首元素
q.pop();//出队
if(b.x==endx&&b.y==endy)//判断是否到达目标位置
{
f=1;//到达目标点
cout<=0&&tx<=4&&ty>=0&&ty<=4&&a[tx][ty]!=1&&v[tx][ty]==0)//判断下一步是否合理
{
v[tx][ty]=1;//将遍历过的点设置为1
point nb;
nb.x = tx;
nb.y = ty;
q.push(nb);//将下一步入队
}
}
}
if(!f)//要是不能到达目标点就输出-1
cout<<"-1"< 二.bfs算法的应用
1.马的遍历
P1443 马的遍历 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
题目描述
有一个 n×m 的棋盘,在某个点 (x,y) 上有一个马,要求你计算出马到达棋盘上任意一个点最少要走几步。
输入格式
输入只有一行四个整数,分别为 n,m,x,y。
输出格式
一个 n×m 的矩阵,代表马到达某个点最少要走几步(不能到达则输出 −1)。
输入样例:
3 3 1 1
输出样例:
0 3 2
3 -1 1
2 1 4
数据范围
对于全部的测试点,保证1≤x≤n≤400,1≤y≤m≤400。
1.对于这道题,我们要先知道马走日字格,所以要先给马的下一步设置8个方向
int dx[8]={-1,-2,-2,-1,1,2,2,1};
int dy[8]={2,1,-1,-2,2,1,-1,-2};2.先设置一个二维数组a[600][600]先将所有值赋值为-1,用二维数组表示最终答案。
3.套用bfs模板。
下面是AC代码,有详细注释
#include
using namespace std;
int dx[8]={-1,-2,-2,-1,1,2,2,1};
int dy[8]={2,1,-1,-2,2,1,-1,-2};//设置方向
int a[600][600],v[600][600];
queue>k;
int main()
{
int n,m,x,y;
cin>>n>>m>>x>>y;
memset(a,-1,sizeof(a));
a[x][y]=0;//首位置不用移动便到达了,赋值为0
v[x][y]=1;//设置到达过
k.push({x,y});//入队首元素
while(!k.empty()){
int tx=k.front().first;//取出队首第一个元素x
int ty=k.front().second;//取出队首第二个元素y
k.pop();//出队
for(int i=0;i<8;i++)//枚举八个方向
{
int l=tx+dx[i],r=ty+dy[i];
if(l<1||l>n||r<1||r>m||v[l][r]==1) continue;//如果下一步不合理,则跳过。
else
{
v[l][r]=1;//将这个点设置为到达
k.push({l,r});//入队
a[l][r]=a[tx][ty]+1;//到达这个点为上一步+1
}
}
}
//经过上面操作后,可以到达的点都设置为了到达的步数,但是不能到达的点还是原来的-1值
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
printf("%-5d",a[i][j]);//最后按要求打印,大功告成
cout< 2.Meteor Shower S
P2895 [USACO08FEB] Meteor Shower S - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
题目背景:
贝茜听说一场特别的流星雨即将到来:这些流星会撞向地球,并摧毁它们所撞击的任何东西。她为自己的安全感到焦虑,发誓要找到一个安全的地方(一个永远不会被流星摧毁的地方)。
如果将牧场放入一个直角坐标系中,贝茜现在的位置是原点,并且,贝茜不能踏上一块被流星砸过的土地。根据预报,一共有 M 颗流星 (1≤M≤50,000)(1≤M≤50,000) 会坠落在农场上,其中第 i 颗流星会在Ti时刻 Ti(0≤Ti≤1000)砸在坐标为 (Xi,Yi)(0≤Xi≤300,0≤Yi≤300)的格子里。流星的力量会将它所在的格子,以及周围 4 个相邻的格子都化为焦土,当然贝茜也无法再在这些格子上行走。贝茜在时刻 0 开始行动,她只能在第一象限中,平行于坐标轴行动,每 1 个时刻中,她能移动到相邻的(一般是 4 个)格子中的任意一个,当然目标格子要没有被烧焦才行。如果一个格子在时刻 t 被流星撞击或烧焦,那么贝茜只能在 t 之前的时刻在这个格子里出现。 贝茜一开始在 (0,0)。
请你计算一下,贝茜最少需要多少时间才能到达一个安全的格子。如果不可能到达输出 −1。
输入格式:
共 M+1 行,第 1 行输入一个整数 M,接下来的 M+1 行每行输入三个整数分别为 Xi,Yi,Ti。
输出格式:
贝茜到达安全地点所需的最短时间,如果不可能,则为 −1。
1.先设置一个结构体二维数组。
struct node{
int x,y,t,step,v;//x,y为该点位置,t为该点陨石掉落的时间,step为步数,v为是否到达
}p[1021][1021];2.将p数组的值全部设置为-1。
3.数据的预处理,将数组点的x,y,t,赋好值。
for(int i=0;i<=1000;i++){
for(int j=0;j<=1000;j++){
p[i][j].x=i;
p[i][j].y=j;
}
} while(m--){
cin>>x>>y>>t;
for(int i=0;i<5;i++){
int tx=x+dx[i];
int ty=y+dy[i];
if(tx<0||ty<0) continue;
if(p[tx][ty].t==-1||p[tx][ty].t>t) p[tx][ty].t=t;
}
}4.最后套用bfs模板。
下面是AC代码,含注释
#include
using namespace std;
struct node{
int x,y,t,step,v;
}p[1021][1021];
int main()
{
memset(p,-1,sizeof(p));//需要全部赋值一个小于0的数,方便数据预处理。
int m,dx[5]={0,0,1,-1,0},dy[5]={1,-1,0,0,0};//枚举上下左右和不动五种情况
cin>>m;
for(int i=0;i<=1000;i++){//数据预处理
for(int j=0;j<=1000;j++){
p[i][j].x=i;
p[i][j].y=j;
}
}
int x,y,t;
while(m--){
cin>>x>>y>>t;
for(int i=0;i<5;i++){
int tx=x+dx[i];
int ty=y+dy[i];
if(tx<0||ty<0) continue;
if(p[tx][ty].t==-1||p[tx][ty].t>t) p[tx][ty].t=t;
}
}
queuek;
p[0][0].step=0;//题目要求从(0,0)点出发
p[0][0].v=1;//将v设为1
k.push(p[0][0]);//入队
while(!k.empty()){//当队列不为空,则继续遍历
node l=k.front();//取出队首元素
k.pop();
for(int i=0;i<4;i++){
int tx=l.x+dx[i];
int ty=l.y+dy[i];
if(tx<0||ty<0||p[tx][ty].v==1) continue;//走出边界,跳过此次循环
if(p[tx][ty].t==-1)//一旦到达-1,则表明走到安全位置,此时的步数就是最短步数
{
cout< 3.Corn Maze S
P1825 [USACO11OPEN] Corn Maze S - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
题目背景:
奶牛们去一个 N×M 玉米迷宫2≤N≤300,2≤M≤300。迷宫里有一些传送装置,可以将奶牛从一点到另一点进行瞬间转移。这些装置可以双向使用。如果一头奶牛处在这个装置的起点或者终点,这头奶牛就必须使用这个装置。玉米迷宫除了唯一的一个出口都被玉米包围。迷宫中的每个元素都由以下项目中的一项组成:
1.玉米,#表示,不可通过
2.草地,.表示,可以简单通过
3.传送装置,每一对大写字母 A 到 Z 表示
4.出口,=表示
5.起点,@表示
输入格式·:
第一行:两个用空格隔开的整数 N 和 M。第 2∼N+1 行:第 i+1 行描述了迷宫中的第 i 行的(共有M个字符,每个字符中间没有空格)。
输出格式:
一个整数,表示起点到出口所需的最短时间。
输入样例:
5 6 ###=## #.W.## #.#### #.@W## ######
输出样例:
3
这道题也是经典的bfs问题,只是添加了传送门,导致相比于一般的bfs问题复杂化了一点,但是只要把握对传送点的特殊判断,这道题是非常容易解决的。
当我们遍历到传送点时,只需要再对数组进行一次遍历,找到另一个相应的传送点,并且将他入队,但是传送点可以使用多次,所以我们不需要将这个点标为经过,这个是易错点。
if(a[tx][ty]>='A'&&a[tx][ty]<='Z')//遇见传送点,进行特殊处理,将传送点的传送位置入队。
{
for(int i=1;i<=n;i++){
for(int j=0;j<=m;j++){//遍历元素,找到另一个传送点
if(a[i][j]==a[tx][ty]&&(tx!=i||ty!=j))
{
node s;
s.x=i;
s.y=j;
s.step=k.step+1;
q.push(s);//标识好值,入队
}
}
}
}只要掌握好这个易错点,这道题再套用bfs算法模板便可以轻松解决。
下面是完整AC代码,有注释。
#include
using namespace std;
struct node{
int x,y,step;
};//设置结构体
int n,m;
char a[400][400],v[400][400];
int dx[4]={1,-1,0,0},dy[4]={0,0,1,-1};
queueq;
int main()
{
cin>>n>>m;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
cin>>a[i][j];//输入
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
if(a[i][j]=='@')//遍历,找到起点
{
node p;
p.x=i;//记录起点坐标
p.y=j;
p.step=0;
v[i][j]=1;
q.push(p);//将起点入队
while(!q.empty()){
node k=q.front();//获取队头元素
q.pop();
if(a[k.x][k.y]=='=')//到达出口,输出步数,此时为最短步数
{
cout<n||ty<1||ty>m||a[tx][ty]=='#'||v[tx][ty]==1) continue;//到达位置不合理,跳过此次循环。
if(a[tx][ty]>='A'&&a[tx][ty]<='Z')//遇见传送点,进行特殊处理,将传送点的传送位置入队。
{
for(int i=1;i<=n;i++){
for(int j=0;j<=m;j++){//遍历元素,找到另一个传送点
if(a[i][j]==a[tx][ty]&&(tx!=i||ty!=j))
{
node s;
s.x=i;
s.y=j;
s.step=k.step+1;
q.push(s);//标识好值,入队
}
}
}
}
else
{
node f;
f.x=tx,f.y=ty;
v[tx][ty]=1;
f.step=k.step+1;
q.push(f);
}
}
}
}
}
}
}
return 0;
} 关于bfs算法的题目有很多,自行探索可以发现很多趣味。
本篇结束。