质数筛—欧拉筛，一步一步的剖析

本篇我们来一点点剖析欧拉筛算法

首先贴上完整代码（以封装成函数的形式呈现），n为要求质数的范围

#define N 10000000
long long zs[N] = { 0 }, size = 0;
char notzs[N] = { 1,1 };
void Euler_sift(int n)
{
	for (int i = 2; i <= n; i++)
	{
		if (!notzs[i])
			zs[size++] = i;
		for (int j = 0; j < size; j++)
		{
			if (zs[j] * i > n)
				break;
			notzs[zs[j] * i] = 1;
			if (i % zs[j] == 0)
				break;
		}
	}
}

欧拉筛的时间复杂度为o(n)

欧拉筛的主要功能是筛掉n内的全部合数。

我们一点一点地来看这串代码

#define N 10000000
long long zs[N] = { 0 }, size = 0;
char notzs[N] = { 1,1 };

zs[N]是一个用来存放筛出来的质数的数组，使用long long类型是为了能存放筛出来的比较大的质数。size是后续用来记录筛出来的质数存到了数组中的第几个位置，同时还能记录筛出来了多少个质数。

notzs[N]是一个用来筛掉非质数下标的数组，比如说某个下标对应的值为真就代表这里不是质数，反之。我们知道0和1不是质数，于是我们在数组初始化的时候就顺便把这两个位置赋值为1也就是把0和1筛掉了。

而之所以用char类型来创建这个数组是因为这个数组只是为了划掉非质数的下标，起到类似flag的效果，无论用什么类型的数组都能达到这个效果，而用char来创建的话能更节约空间。

	for (int i = 2; i <= n; i++)

由于我们已经给notzs数组下标为0和1的元素初始化（筛掉）了，所以我们的循环从下标为2的位置开始，对闭区间n范围内的数来筛质数。

		if (!notzs[i])
			zs[size++] = i;

我们一上来就对循环变量i对应的下标位置进行判断，如果下标i对应的notzs数组的值为0(假)时，也就是没有被筛掉的位置，我们就把这个位置的下标存到zs数组内，存下来的这个下标就是一个素数了。存完的同时size自增指向zs数组的下一个位置。

		for (int j = 0; j < size; j++)
		{
			if (zs[j] * i > n)
				break;
			notzs[zs[j] * i] = 1;
			if (i % zs[j] == 0)
				break;
		}

接下来就是重点，筛质数部分。这每一次循环只要没满足break的条件就都会把已经存下来的质数走一遍。

里面的三个语句的顺序是非常重要的。

			if (zs[j] * i > n)
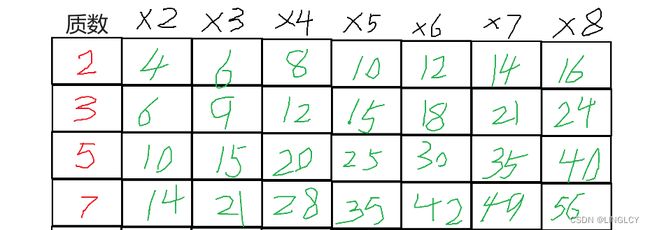
				break;

一上来就先判断即将要划掉(筛掉)的数是否越界，如果要划掉(筛掉)的数已经超过了我们想的范围的话就没意义了吧，而且会增加时间复杂度。而这个需要划掉(筛掉)的数就是一个质数的倍数，因为质数的倍数一定不是质数。n内的合数一定是n内质数的倍数！

			notzs[zs[j] * i] = 1;

接下来就是划掉(筛掉)质数的倍数

就像上面这样，这些数都是要被划掉(筛掉)的。

但是我们发现有很多数都会被重复划掉(筛掉)，比如说上面这些蓝框框框起来的，看的越远重复的数就越多。如果这样放任他重复划掉(筛掉)的话是很浪费时间的，而我们的下一行代码就是用来阻止他这么做的。

			if (i % zs[j] == 0)
				break;

当i为已经存下来的第j个质数的倍数的时候就会跳出循环。

这么一来我们前八次循环就会划掉(筛掉)这些数，同时我们发现不再出现重复划掉(筛掉)的情况。效率upup。

到这里关于欧拉筛的要点就已经全部讲完了。希望大家都能看懂吧。