2021牛客寒假算法基础集训营1

2021牛客寒假算法基础集训营1

咕了好久~~

A 串

分析：
利用动态规划，当时没想到动态规划，还想找找规律什么的，看看都是重复几个，然后前缀和的。
用dp[i][0/1/2]表示长度为i的 没有u的串/有u但是u后面没有s的串/有us的串的数量
然后状态转移方程就是

	dp[i][0] = (dp[i - 1][0] * 25) % mod;
	//在原来没有u的后面加上除了u以外的25个字母
    dp[i][1] = (dp[i - 1][1] * 25 + dp[i - 1][0]) % mod;
    //原来有u的后面加上除了s以外的任意一个字母，原来没有的加上u
    dp[i][2] = (dp[i - 1][1] + dp[i - 1][2] * 26) % mod;
    //原来有u的后面加上s，原来就有us的后面加上26个字母任意一个

涉及知识点
动态规划
AC代码

#include 

using namespace std;
typedef long long ll;

ll dp[1000050][5];
int n;
int mod = 1000000007;
ll ans;

int main()
{
    scanf("%d", &n);
    //注意初始化
    dp[1][0] = 25;
    dp[1][1] = 1;
    dp[1][2] = 0;

    for(int i = 2; i <= n; ++i)
    {
        dp[i][0] = (dp[i - 1][0] * 25) % mod;
        dp[i][1] = (dp[i - 1][1] * 25 + dp[i - 1][0]) % mod;
        dp[i][2] = (dp[i - 1][1] + dp[i - 1][2] * 26) % mod;
        ans = (ans + dp[i][2]) % mod;
    }
    printf("%d\n", ans);
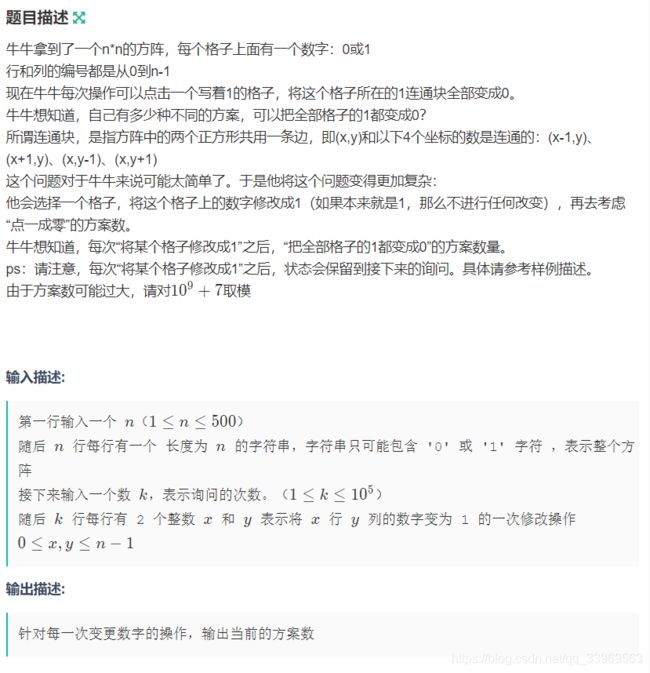
    return 0;
}

B 括号

分析：
我的做法是a = sqrt（k），然后a个左括号，a个右括号，还差b = k - a * a对括号，这b对括号，只需要在第一个左括号后面放b个右括号即可。但是这样长度在最大的时候还是会超，所以再对b做一次同样的操作。
AC代码：
（写的很乱，有时间重新写吧）

#include 

using namespace std;

int k;
string s1[10], s2[10];
int a, x, y, s;

void deal()
{
    s1[0] = "(";
    s2[0] = ")";
    for(int i = 1; i <= 5; ++i)
    {
        for(int j = 1; j <= 10; ++j)
        {
            s1[i] += s1[i - 1];
            s2[i] += s2[i - 1];
        }
        //cout << s2[i] << endl;
    }
}

int main()
{
    deal();
    scanf("%d", &k);
    if(k == 0)
    {
        cout << "))))))))))))))(((((((((\n";
        return 0;
    }
    a = sqrt(k);
    s = k - a * a;
    //cout << s  << endl;
    putchar('(');
    int sum = 1;

    x = sqrt(s);
    int temp = x;
    y = s - x * x;
    while(y >= 1000)
    {
        cout << s2[3];
        y -= 1000;
        sum += 1000;
    }
    while(y >= 100)
    {
        cout << s2[2];
        y -= 100;
        sum += 100;
    }
    while(y >= 10)
    {
        cout << s2[1];
        y -= 10;
        sum += 10;
    }
    while(y > 0)
    {
        cout << s2[0];
        y--;
        sum++;
    }

    int xx = x - 1;
    while(xx >= 1000)
    {
        cout << s1[3];
        xx -= 1000;
        sum += 1000;
    }
    while(xx >= 100)
    {
        cout << s1[2];
        xx -= 100;
        sum += 100;
    }
    while(xx >= 10)
    {
        cout << s1[1];
        xx -= 10;
        sum += 10;
    }
    while(xx > 0)
    {
        cout << s1[0];
        xx--;
        sum ++;
    }

    while(x >= 1000)
    {
        cout << s2[3];
        x -= 1000;
        sum += 1000;
    }
    while(x >= 100)
    {
        cout << s2[2];
        x -= 100;
        sum += 100;
    }
    while(x >= 10)
    {
        cout << s2[1];
        x -= 10;
        sum += 10;
    }
    while(x > 0)
    {
        cout << s2[0];
        x--;
        sum ++;
    }

    int aa;
    if(temp == 0)   aa = a - 1;
    else    aa = a - temp;
    //cout << aa << endl;
    while(aa >= 1000)
    {
        cout << s1[3];
        aa -= 1000;
        sum += 1000;
    }
    while(aa >= 100)
    {
        cout << s1[2];
        aa -= 100;
        sum += 100;
    }
    while(aa >= 10)
    {
        cout << s1[1];
        aa -= 10;
        sum += 10;
    }
    while(aa > 0)
    {
        putchar('(');
        aa--;
        sum++;
    }
    //cout << a << endl;

    while(a >= 10000)
    {
        cout << s2[4];
        a -= 10000;
        sum += 10000;
    }
    while(a >= 1000)
    {
        cout << s2[3];
        a -= 1000;
        sum += 1000;
    }
    while(a >= 100)
    {
        cout << s2[2];
        a -= 100;
        sum += 100;
    }
    while(a >= 10)
    {
        cout << s2[1];
        a -= 10;
        sum += 10;
    }
    while(a > 0)
    {
        putchar(')');
        a--;
        sum++;
    }
    //cout << '\n' << sum << endl;
    //cout << s2[5] << endl;
    return 0;
}

C 红和蓝

额，先跳过

D 点一成零

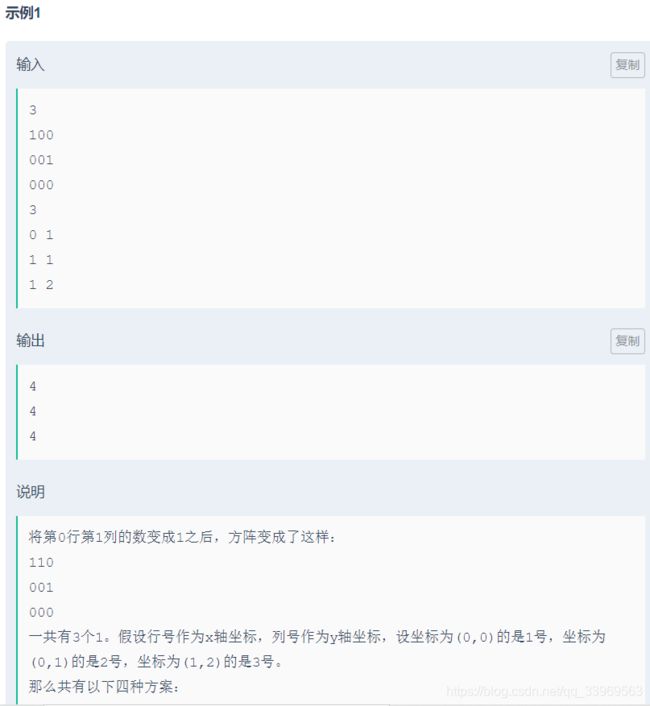
分析：
这个题用并查集是真妹想到袜，先对没修改过的方阵使用秘技
·并查集，假设他不修改，那么方案数就是合并后的块数的阶乘乘上每块的大小。
如果修改，可能出现三种情况：
1.这个点本来就是1，那什么也妹发生
2.这个点本来是0，改了之后这个点单独一个集合，即这个点的上下左右都是0
3.这个点本来是0，改了之后又和其他集合合并了。
对于这三种情况：
情况1不用管，情况二的话需要在原本的基础上乘方案数加一（阶乘多了嘛），情况三的话先修改阶乘，方案数可能会减少要除以几个数还要取模，要用到逆元，然后每块的大小有几块变了，要先除掉，再乘上去（有点语无伦次）
涉及知识点：
逆元，并查集
逆元：

	(a / b) % p = (a * c) % p;
	//其中c是a的逆元，c = a^(p - 2),p要是质数

AC代码：

#include 

using namespace std;
typedef long long ll;
int n, k, x, y;
int dir[4][2] = {1, 0, -1, 0, 0, -1, 0, 1};//四个方向上下左右
int dx, dy;
int mod = 1e9 + 7;
char ch[505][505];
const ll MAXN = 250050;

int ufs[MAXN];
int sum[MAXN];
void Init(int n)
{
    int i;
    for(i=0;i<=n;i++)//初始化0~n，可能会出现边界情况，所以把0弄进去了
    {
        ufs[i] = i;
        sum[i] = 1;
    }
}

int GetRoot(int a)
{
    if(ufs[a]!=a)
    {
        ufs[a] = GetRoot(ufs[a]);
    }
    return ufs[a];
}

void Merge(int x,int y)
{
    int fx = GetRoot(x);
    int fy = GetRoot(y);
    if(fx != fy)
    {
        sum[fx] += sum[fy];
        ufs[fy] = fx;
    }
}

bool Query(int a,int b)
{
    return GetRoot(a)==GetRoot(b);
}

ll pow_mod(ll a, ll n, ll m)//快速幂
{
    ll ans = 1;
    a %= m;
    while(n)
    {
        if(n & 1)
        {
            ans = (ans * a) % m;
        }
        a = (a * a) % m;
        n >>= 1;
    }
    return ans;
}

ll ni(int x)//求逆元
{
    return pow_mod(x, mod - 2, mod);
}

int main()
{
    scanf("%d", &n);
    for(int i = 1; i <= n; ++i) scanf("%s", ch[i] + 1);
    //因为数据是ch[i][j]二维数组读进来的，再并查集数组中ch[i][j]对应ufs[(i - 1) * n + j]
    Init(n * n);
    //扫描这个数组进行合并
    for(int i = 1; i <= n; ++i)
    {
        for(int j = 1; j <= n; ++j)
        {
            if(ch[i][j] == '1')
            {
                if(ch[i - 1][j] == '1')  Merge((i - 1) * n + j, (i - 2) * n + j);
                if(ch[i + 1][j] == '1')  Merge((i - 1) * n + j, i * n + j);
                if(ch[i][j - 1] == '1')  Merge((i - 1) * n + j, (i - 1) * n + j - 1);
                if(ch[i][j + 1] == '1')  Merge((i - 1) * n + j, (i - 1) * n + j + 1);
            }
        }
    }

    int cnt = 0;//cnt存有几块
    ll ans = 1;//ans就是答案
    for(int i = 1; i <= n; ++i)
    {
        for(int j = 1; j <= n; ++j)
        {
            if(ufs[(i - 1) * n + j] == (i - 1) * n + j && ch[i][j] == '1')
            {
                cnt++;
                ans = (ans * sum[(i - 1) * n + j]) % mod;//先把每块的大小乘进来
            }
        }
    }

    for(int i = 1; i <= cnt; ++i)   ans = (ans * i) % mod;//阶乘

    scanf("%d", &k);
    while(k--)
    {
        scanf("%d %d", &x, &y);

        x++, y++;//题目中这两个数是0~n-1的，需要加1
        if(ch[x][y] == '1')
        {
            printf("%lld\n", ans);//情况1
            continue;
        }
        //其他两种情况都是一开始是0，我们先变0为1，并将方案数加1（假设是情况2）
        ch[x][y] = '1';
        cnt++;
        ans = ans * cnt % mod;//修改答案
        //判断四个方向
        for(int i = 0; i < 4; ++i)
        {
            dx = x + dir[i][0];
            dy = y + dir[i][1];
            //如果这个方向是1
            if(ch[dx][dy] == '1')
            {
                int f1 = GetRoot((x - 1) * n + y);
                int f2 = GetRoot((dx - 1) * n + dy);
			//并且不在一个集合里，我们需要先除掉方案数，因为总方案数-1了
			//再分别除掉这两个集合的大小，然后乘上新的集合的大小
			//并将集合数--，以及合并两个集合
                if(f1 != f2)
                {
                    ans = ans * ni(cnt) % mod;
                    ans = ans * ni(sum[f1]) % mod;
                    ans = ans * ni(sum[f2]) % mod;
                    ans = ans * (sum[f1] + sum[f2]) % mod;
                    cnt--;
                    Merge(f1, f2);
                }
            }
        }
        printf("%lld\n", ans);
    }
    return 0;
}

E 三棱锥之刻

数学题啊，我溜了~

F 对答案一时爽

签到题。

G 好玩的数字游戏

模拟模拟模拟，溜了~

H 幂塔个位数的计算

分析：
因为这个数很大我们可以想到他可能只和a的最后一位有关。
据雨巨的讲解以及自己的瞎推大约是懂了

（有个地方推的不对啊，懒得改了）

AC代码

#include 

using namespace std;

int a, b, len;//a是最后以为，b是%4的值，len是s1的长度
string s1, s2;

int main()
{
    cin >> s1 >> s2;
    len = s1.size();
    if(s2.size() == 1 && s2[0] == '1')//s2为1的时候直接输出
    {
        cout << s1[len - 1] << '\n';
        return 0;
    }
	
	//对于那些4个一循环的我们需要知道a%4是几，而这个值只与a的最后两位有关
    b = ((s1[len - 2] - '0') * 10 + s1[len - 1] - '0') % 4;
    a = s1[len - 1] - '0';

    if(a == 0 || a == 1 || a == 5 || a == 6 || a == 9)
    {
        cout << a << '\n';
        return 0;
    }
    if(a == 4)
    {
        cout << 6 << '\n';
        return 0;
    }
    if(a == 2 || a == 8)
    {
        if(s2.size() == 1 && s2[0] == '2' && b != 0)    cout << 4 << '\n';
        else    cout << 6 << '\n';
        return 0;
    }
    if(a == 3)
    {
        if(b == 1)  cout << 3 << '\n';
        else        cout << 7 << '\n';
    }
    if(a == 7)
    {
        if(b == 3)  cout << 3 << '\n';
        else        cout << 7 << '\n';
        return 0;
    }
}

I 限制不互素对的排列

分析：
这个题本身挺简单的靠偶数和6，3即可但要注意正好k个别弄多了，然后雨巨提的那个问题有时间自己写写哈
AC代码：

#include 

using namespace std;

int n, k;
int x = 1;
bool vis[100050];

int main()
{
    scanf("%d %d", &n, &k);
    if((n == 2 && k == 1)|| (n == 3 && k == 1)|| (n == 4 && k == 2)||(n == 5 && k == 2))
    {
        printf("-1");
        return 0;
    }
    else if(k == 0)
    {
        printf("1");
        for(int i = 2; i <= n; ++i) printf(" %d", i);
        printf("\n");
    }
    else if(k == 1)
    {
        printf("2 4");
        vis[2] = 1;
        vis[4] = 1;
        for(int i = 1; i <= n; ++i)
        {
            if(!vis[i]) printf(" %d", i);
        }
    }
    else
    {
        printf("3 6");
        k--;
        vis[3] = 1;
        vis[6] = 1;
        for(int i = 2; i <= n; i += 2)
        {
            if(k == 0)  break;
            if(!vis[i])
            {
                printf(" %d", i);
                vis[i] = 1;
                k--;
            }
        }
        for(int i = 1; i <= n; ++i)
        {
            if(!vis[i]) printf(" %d", i);
        }
    }
}

J 一群小青蛙呱蹦呱蹦呱

分析：
只有某个数它有两个及其以上的质因子才不会别次掉，假设剩下n个数没被吃掉，把这n个数质因数分解：
a1 = p1^c11 * p2^c21 * p3^c31 *…*pm^cm1
a2 = p1^c12 * p2^c22 * p3^c32 *…*pm^cm2
…
an = p1^c1n * p2^c2n * p3^c3n *…*pm^cmn
最后lcm = p1^max(c11,c12,c13,…,c1n) * p2^max(c21,c22,c23,…,c2n) * … * pm^max(cm1,cm2,…,cmn);
首先p1到pm就是2到n/2内的所有质数，因为要求最大的lcm且这个数至少由两个质因子，所以让一个质因子为2来保证另一个尽可能的大。其次，对于指数，以2的指数为例，2^n * 一坨数 = n，很明显要让n最大，求要让那一坨数尽可能的小，所以那一坨数 = 3，对于其他的数，那一坨数就等于2.
涉及知识点：
线性筛，快速幂
AC代码

#include 

using namespace std;
typedef long long ll;

const int N = 8e7, mod = 1e9 + 7;
int v[N], prime[N], tot;
int n;
ll ans = 1;

//快速幂
ll pow_mod(ll a, ll n, ll m)
{
    ll ans = 1;
    a %= m;
    while(n)
    {
        if(n & 1)
        {
            ans = (ans * a) % m;
        }
        a = (a * a) % m;
        n >>= 1;
    }
    return ans;
}

//线性筛
void Prime(int n)
{
    for(int i = 2; i <= n; ++i)
    {
        if(!v[i])   v[i] = prime[++tot] = i;
        for(int j = 1; j <= tot; ++j)
        {
            if(prime[j] > v[i] || prime[j] > n / i) break;
            v[i * prime[j]] = prime[j];
        }
    }
}

//求以v为底n/u的对数，用的是换底公式求的好像（数学不好。。。）
int calc(int u, int v)
{
    return log(n / u) / log(v);
}

int main()
{
    scanf("%d", &n);

    Prime(n / 2);
    ans = ans * pow_mod(2, calc(3, 2), mod) % mod;
    for(int i = 2; i <= tot; ++i)   ans = ans * pow_mod(prime[i], calc(2, prime[i]), mod) % mod;
    if(ans == 1)    printf("empty\n");
    else            printf("%d\n", ans);
    return 0;
}