题目练习(生死时速2.0版)
题目一(Before an Exam)
题意翻译
题目背景
明天皮特将要考生物。他并不很喜欢生物,但在 d 天前他得知他将不得不参加此次考试。皮特严厉的父母勒令他立即复习,因此他在第 i 天将需要学习不少于 minTimei 小时,不多于 maxTimei 小时。他们同时警告皮特:考试前一天,他将被检查他复习的完成情况。
因此,今天皮特的父母会要求他展示他考前复习的学习时间表。然而,他只记录这 d 天以来他复习所用的总计用时sumTime(小时).现在他希望知道他能否给他的父母展示一份时间表,包含 d 个数,每个数 schedulei 表示皮特第 i 天在复习生物上的用时(单位为小时),并应满足上文提及的要求。
题目输入
第一行包含两个数:d,sumTime。
(1≤d≤30,0≤sumTime≤240),意义如上所述。
接下来 d 行,每行两个数:minTimei,maxtimei,两个数之间有一个空格,意义如上。(0≤minTimei≤maxTimei≤8)
题目输出
如果有解,在单独一行输出 YES,换行,输出任意一种满足上文要求的解。如果无解,在单独一行中输出 NO。
输入输出样例
输入 #1复制
1 48
5 7输出 #1复制
NO
输入 #2复制
2 5
0 1
3 5输出 #2复制
YES
1 4 代码实现:
#include
struct fun
{
int max;
int min;
int cha;
}time[40];
int main()
{
int d, sumtime;
scanf("%d%d", &d, &sumtime);
int p1 = 0, p2 = 0;
for (int i = 1; i <= d; i++) {
scanf("%d%d", &time[i].min, &time[i].max);
p1 += time[i].max;
p2 += time[i].min;
time[i].cha = time[i].max - time[i].min;
}
if (sumtimep1) {
printf("NO\n"); return 0;
}
else printf("YES\n");
int f = 0;
int p3 = sumtime - p2;
if (p3 != 0) {
for (int i = 1; i <= d; i++) {
for (int j = 1; j <= time[i].cha; j++) {
time[i].min++;
p3--;
if (p3 == 0) {
f = 1; break;
}
}
if (f == 1)break;
}
}
for (int i = 1; i <= d; i++) {
printf("%d ", time[i].min);
}
return 0;
} 结果:
 样例一
样例一
题目二(最大子段和)
题目描述
给出一个长度为 n 的序列 a,选出其中连续且非空的一段使得这段和最大。
输入格式
第一行是一个整数,表示序列的长度 n。
第二行有 n 个整数,第 i 个整数表示序列的第 i 个数字 ai。
输出格式
输出一行一个整数表示答案。
输入输出样例
输入 #1复制
7
2 -4 3 -1 2 -4 3输出 #1复制
4
说明/提示
样例 1 解释
选取 [3,5][3,5] 子段 {3,−1,2}{3,−1,2},其和为 4。
数据规模与约定
- 对于 40%40% 的数据,保证 �≤2×103n≤2×103。
- 对于 100%100% 的数据,保证 1≤�≤2×1051≤n≤2×105,−104≤��≤104−104≤ai≤104。
代码实现:
#include
using namespace std;
int maxx = -3333333;
int main()
{
int n, a, b;
scanf("%d", &n);
for (int i = 1; i <= n; i++) {
scanf("%d", &a);
if (i == 1)b = a;
else b = max(a, a + b);
maxx = max(maxx, b);
}
printf("%d", maxx);
return 0;
} 题目三(KMP)
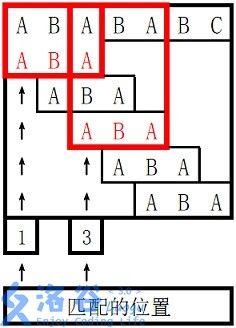
题目描述
给出两个字符串 s1 和 s2,若 s1 的区间 [l,r] 子串与 s2 完全相同,则称 s2 在 s1 中出现了,其出现位置为 l。
现在请你求出 s2 在 s1 中所有出现的位置。
定义一个字符串 s 的 border 为 s 的一个非 s 本身的子串 t,满足 t 既是 s 的前缀,又是 s 的后缀。
对于 s2,你还需要求出对于其每个前缀 ′s′ 的最长 border ′t′ 的长度。
输入格式
第一行为一个字符串,即为 s1。
第二行为一个字符串,即为 s2。
输出格式
首先输出若干行,每行一个整数,按从小到大的顺序输出 s2 在 s1 中出现的位置。
最后一行输出 ∣s2∣ 个整数,第 i 个整数表示 s2 的长度为 i 的前缀的最长 border 长度。
输入输出样例
输入 #1复制
ABABABC
ABA输出 #1复制
1
3
0 0 1 说明/提示
样例 1 解释
。
对于 s2 长度为 3 的前缀 ABA,字符串 A 既是其后缀也是其前缀,且是最长的,因此最长 border 长度为 11。
数据规模与约定
本题采用多测试点捆绑测试,共有 3 个子任务。
- Subtask 1(30 points):∣s1∣≤15,∣s2∣≤5。
- Subtask 2(40 points):∣s1∣≤104,∣s2∣≤102。
- Subtask 3(30 points):无特殊约定。
代码:
#include
#include
#define MAX 1000100
using namespace std;
int KMP[1000100], len1, len2;
char a[MAX], b[MAX];
int main()
{
scanf("%s%s", a+1, b+1);
len1 = strlen(a+1);
len2 = strlen(b+1);
int j = 0;
for (int i = 2; i <= len2; i++) {
while (j && b[i] != b[j + 1])j = KMP[j];
if (b[j + 1] == b[i])j++;
KMP[i] = j;
}
j = 0;
for (int i = 1; i <= len1; i++) {
while (j > 0 && b[j + 1] != a[i])j = KMP[j];
if (b[j + 1] == a[i])j++;
if (j == len2) {
printf("%d\n", i - len2 + 1);
j = KMP[j];
}
}
for (int i = 1; i <= len2; i++)
printf("%d ", KMP[i]);
return 0;
}