leetCode二叉树的堂兄弟节点 II

题目

给你一棵二叉树的根 root ，请你将每个节点的值替换成该节点的所有 堂兄弟节点值的和 。

如果两个节点在树中有相同的深度且它们的父节点不同，那么它们互为 堂兄弟 。

请你返回修改值之后，树的根 root 。

注意，一个节点的深度指的是从树根节点到这个节点经过的边数。

示例 1：

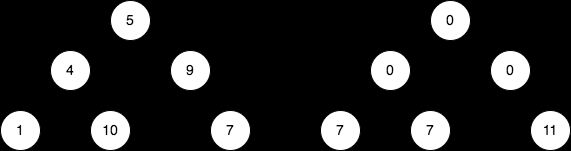
输入：root = [5,4,9,1,10,null,7]
输出：[0,0,0,7,7,null,11]
2641. 二叉树的堂兄弟节点 II

本题思路

这题思路其实是比较简单的，就是找到同层的节点，然后让非同父的节点相加即可。

这样我们就需要记录父节点，本节点的值。

于是出现了下面的代码

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    List> lists=new ArrayList<>();
    public TreeNode replaceValueInTree(TreeNode root) {
        dfs(root,null,0,true);//进行两次遍历，第一次记录层数记录
        dfs(root,null,0,false);//第二次进行累加
        return root;
    }

    public void dfs(TreeNode p,TreeNode f,int l,boolean b){
        if(p!=null){
            if(b){
                if(lists.size()<=l)
                    lists.add(new ArrayList<>());
                lists.get(l).add(new Tree(p.val,f));
            }
            else{
                int sum=0;
                for(int i=0;i

结果不出意外的超出时间限制了，问题也很简单出现在二次遍历中的for循环当中。于是开始尝试优化，既然遍历其他同层的太过于冗余麻烦，那么我可以将同层的所有相加，而后再减去同父的节点值不就可以了。于是出现了下面的代码

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    List lists=new ArrayList<>();
    public TreeNode replaceValueInTree(TreeNode root) {
        dfs(root,0,true,0);//同样的两次循环，不过第一次不是记录，而是统计同层的值
        dfs(root,0,false,0);//第二次进行减去
        return root;
    }

    public void dfs(TreeNode p,int l,boolean b,int f){
        if(p!=null){
            if(b){//累加
                if(lists.size()<=l)
                    lists.add(0);
                lists.set(l,lists.get(l)+p.val);
            }
            else{//减去
                p.val=lists.get(l)-f-p.val;
            }
            int lp=p.left==null?0:p.left.val;//因为引用修改的关系，所以需要提前复制
            dfs(p.left,l+1,b,p.right==null?0:p.right.val);
            dfs(p.right,l+1,b,lp);
        }
    }
}

最后成功通过，但其实完全可以使用bfs来进行优化编写，将会更加的省空间。