算法--树状数组与线段树
树状数组与线段树
- 前言
- 概念
-
- 前缀和
-
- 代码模板
- 线段树
-
- 代码模板
- 练习题
-
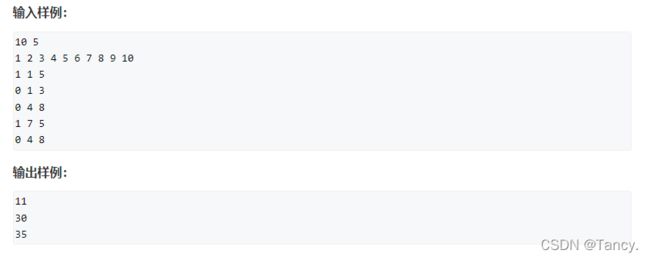
- 动态求连续区间和
- 数星星 -- 树状数组
- 数列区间最大值 -- 线段树
算法基础系列
前言
本节知识点较难,且模板代码较长,可根据自己情况理解
这里只浅析树状数组 更深层次的内容不会涉及
概念
前缀和
因为画出的结构特别像树,因此得名 树状数组

定义: C [ x ] = ( x − l o w b i t ( x ) , x ] C[x]=(x-lowbit(x),x] C[x]=(x−lowbit(x),x] 左闭右开
lowbit(x) = x & -x = 2 k 2^k 2k
递归处理
树状数组解决的两个问题:
1. 单点查询: 在某个位置上加上一个树
2. 区间更新:求某一个区间前缀和
总的来说:树状数组是一个可以支持快速进行单点修改和区间查询的数据结构
修改:只修改和该节点相关的节点
与前缀和的关键区别
可查询动态修改的数组
lowbit(x)是什么?
表示:x在二进制下最右边的第一个1对应的十进制是多少
1 对应的二进制是 -> 1 最右边1对应的10进制 -> 1
2 对应的二进制是 -> 10 最右边1对应的10进制 -> 2
3 对应的二进制是 -> 11 最右边1对应的10进制 -> 1
4 对应的二进制是 -> 100 最右边1对应的10进制 -> 4
5 对应的二进制是 -> 101 最右边1对应的10进制 -> 1
6 对应的二进制是 -> 110 最右边1对应的10进制 -> 2
······
lowbit(1) = 1
lowbit(2) = 2
lowbit(3) = 1
lowbit(4) = 4
lowbit(5) = 1
lowbit(6) = 2
······
lowbit(x) = (x) & (-x)
证明略
代码模板
// 求最低的一位1
int lowbit(int x){
return x & -x;
}
// 更新操作 在tr[x]的位置加上c
void add(int x, int c){
for(int i = x; i <= n; i += lowbit(i)) tr[i] += c;
}
// 求前缀和
int query(int x){
int res = 0;
for(int i = x; i > 0; i -= lowbit(i)) res += tr[i];
return res;
}
线段树
这是一个完全二叉树
操作:
- 单点修改 O ( log n ) O(\log{n}) O(logn)
- 区间查询(递归过程) O ( log n ) O(\log{n}) O(logn)
线段树这种数据结构可以很好的处理区间查询和区间修改的问题,虽然树状数组也可以通过差分的思想来实现区间修改,但是树状数组通常只能用于区间求和,而线段树能够处理区间最大值/最小值等一系列问题
线段树虽然看起来是一个树状结构,但是我们通常使用数组来保存线段树,假设我们原是数组的大小为 n n n,则开辟的空间大小为 4 ∗ n 4 * n 4∗n
简短证明:线段树所有叶子节点必然在最下面的两层中。考虑倒数第二层的节点,其个数一定小于 n n n,那么从倒数第二层一直到根节点的节点数一定小于 2 n 2n 2n,最后一层的节点数最多是是倒数第二层的两倍,那么也小于 2 n 2n 2n,所以总共小于 4 n 4n 4n
有四个函数操作
pushup更新操作,因为是递归操作,有回溯build建树 在一段区间上初始化modify修改query查询
关于父子节点
父节点: ⌊ x 2 ⌋ \lfloor \frac x2 \rfloor ⌊2x⌋ x >> 1
左子节点 : 2 x 2 x 2x x << 1
右子节点: 2 x + 1 2 x +1 2x+1 x << 1 | 1
代码模板
struct Node
{
int l, r;
int sum;
} tr[N * 4];
void pushup(int u) //更新结点值 向上更新
{
//左儿子的sum + 右儿子的 sum
tr[u].sum = tr[u << 1].sum + tr[u << 1 | 1].sum;
}
void build(int u, int l, int r)// 建树
{
if (l == r) tr[u] = {l, r, w[l]}; //赋值 如果是叶节点 sum是本身
else
{
tr[u] = {l, r};
int mid = l + r >> 1; //分成两边
build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r); //递归处理左右儿子
// u << 1 是左儿子 u << 1 | 1 是 右儿子
pushup(u); //因为值发生了改变,向上更新值
}
}
int query(int u, int l, int r) //求区间和
{
if (tr[u].l >= l && tr[u].r <= r)
return tr[u].sum; // 如果所求区间在该节点的范围内 直接返回sum
//如果不在 递归找
int mid = tr[u].l + tr[u].r >> 1;
int sum = 0;
if (l <= mid)
sum = query(u << 1, l, r);
if (r > mid)
sum += query(u << 1 | 1, l, r);
return sum;
}
void modify(int u, int x, int v) //修改
{
if (tr[u].l == tr[u].r) tr[u].sum += v;
else
{
int mid = tr[u].l + tr[u].r >> 1;
if (x <= mid) //在mid的左边
modify(u << 1, x, v);
else modify(u << 1 | 1, x, v);
pushup(u); //修改完后更新值
}
}
练习题
动态求连续区间和
模板题
树状数组和线段树都能用
树状数组
#include 线段树
#include 数星星 – 树状数组
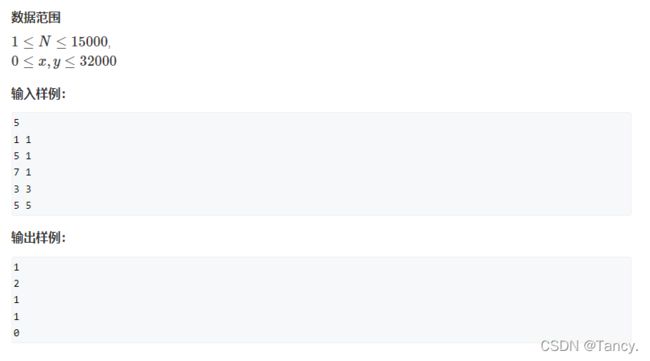
数星星

思路
暴力 – 优化 – 学以致用
1、题目要求求某一个点(x,y)左下方星星的个数(不包括自己),且星星按y坐标增序给出,y 坐标相同的按x坐标增序给出,因此对于每个新来的点(x,y),y是当前纵坐标的最大值,只需要求[1,x]中星星出现的数量即可
2、通过树状数组完成单点修改,区间查询操作
注意:树状数组是从1开始的,而题目的给定的x范围是0≤x≤32000,因此需要将所有的x赋值成x + 1(相对位置不变)
#include 数列区间最大值 – 线段树
#include 更多练习题写完再更······