趣学贝叶斯统计：逻辑与二项分布

前言

高中时概率与统计中，大家学过逻辑符号、二项分布。今天我们重新复习一下基本知识，系统梳理推导过程，并稍微进阶到代码和库的运用中。

关键词：

AND OR BUT
二项分布
概率质量函数（probability mass function，PMF）
累计分布函数(Cumulative Distribution Function, CDF)

第三章 逻辑

AND: $P(A,B)=P(A)\ast P(B)$

• 扩展：$$P((A,B),C)=P(A,B)\ast P(C)=P(A)\ast P(B)\ast P(C)$$

OR:
(1)互斥：一个事件发生意味着其他事件不可能发生。只要事件是互斥的，就可以直接将每个可能事件的概率相加而得到任一事件发生的概率，从而计算出一个事件OR另一个事件的概率
①$P(A,B)=0$
②$P(AORB)=P(A)+P(B)$
(2)非互斥事件：
$P(AORB)=P(A)+P(B)-P(A,B)$
NOT: $\neg P(X)=1-P(X)$

第四章 创建二项分布

1. 二项分布的结构

二项分布中的“二项”是指每次实验只有两个可能结果：一个事件发生和一个事件没有发生。如果有两个以上的结果，则称为多项分布（multinomial distribution）。
$$B(k;n,p)$$

k=我们关心的事件的发生次数
p=一次事件成功的概率
n=试验次数

e g .计算3次掷硬币实验中出现2次正面的概率.
k=2
p=$\frac{1}{2}$
n=3

3次掷硬币中出现2次正面的结果有3种可能：
正正反, 正反正, 反正正
这三种结果不会同时出现，是互斥事件。所以有：
①$P(\{正正反\})=P(\{正反正\})=P(\{反正正\})$
②$P(\{正正反\},\{正反正\},\{反正正\})=0$

使用概率的加法法则，$3\ast P(期望结果)$
$$B(k;n,p)=n\ast p$$

2.组合学（combinatorics）

从n个中选择k: $\left(\genfrac{}{}{0ex}{}{n}{k}\right)=\frac{n!}{k!(n-k)!}$
大多数数学编程语言用choose()函数来计算二项式系数，例如在R语言中，可以调用下面的语句来计算3次掷硬币出现2次正面时的二项式系数：

choose(3,2)

通用计算结果：
$$B(k;n,p)=\left(\genfrac{}{}{0ex}{}{n}{k}\right)\ast P(期望结果)$$

3. 计算期期望结果概率

eg.在5次掷硬币实验中出现2次正面的概率
情况：正面, 正面, 非正面, 非正面, 非正面
$$P(期望结果)=P(正面{)}^2\ast (1-P(正面){)}^3$$

通用结果：
$$B(k;n,p)=\left(\genfrac{}{}{0ex}{}{n}{k}\right)\ast p^k\ast (1-p{)}^{n-k}$$

这个公式是二项分布的基础，它一般被称为概率质量函数（probability mass function，PMF）。“质量”一词来自这样一个事实，即当给定n和p时，可以计算任意k的概率，这就是概率的质量。

4.代码

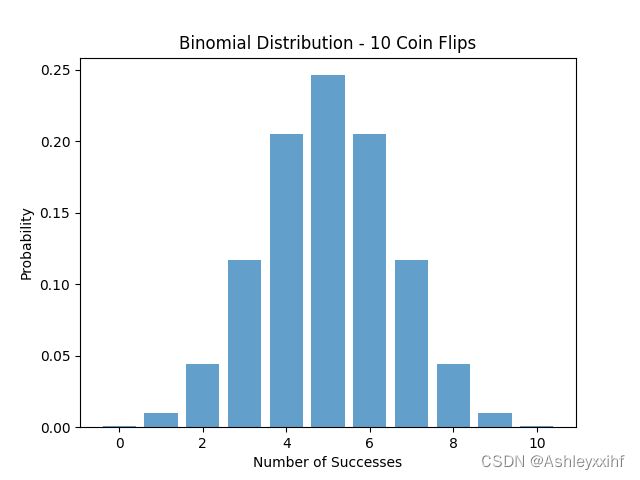
可以把10次掷硬币实验中k的所有可能取值代入到PMF中，并将所有可能值的二项分布可视化.

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import binom #统计库。binom专门计算二项

# 定义二项分布的参数
n = 10  # 试验次数
p = 0.5  # 单次试验成功的概率


k = np.arange(0, n + 1) #k所有可能值
pmf = binom.pmf(k, n, p)

# 可视化二项分布
plt.bar(k, pmf, align='center', alpha=0.7)#align是对齐方式,alpha控制了条形的透明度
plt.title('Binomial Distribution - 10 Coin Flips')
plt.xlabel('Number of Successes')
plt.ylabel('Probability')
plt.show()

10次掷6面骰子实验中，扔出六点k次的概率：

累计分布函数CDF：
$$\sum _{i=0}^k{a}_i$$

$$P(X\le K)=\sum _{i=0}^k\left(\genfrac{}{}{0ex}{}{n}{i}\right)p^i(1-p{)}^{n-i}$$

表示在 n 次试验中选择 i 次成功的不同组合的数量。上述公式表示从 i=0 到 k 的所有可能取值的概率质量函数之和，即累积分布函数

总结

在本章中，我们看到可以使用概率规则（结合组合学中的一个技巧）构建出通用的方法，来解决一整类的概率问题。对于任何涉及在n次实验中出现k次结果的概率问题，其中结果的发生概率为$B(k;n,p)=\left(\genfrac{}{}{0ex}{}{n}{k}\right)\ast p^k\ast (1-p{)}^{n-k}$，都可以使用二项分布轻松解决