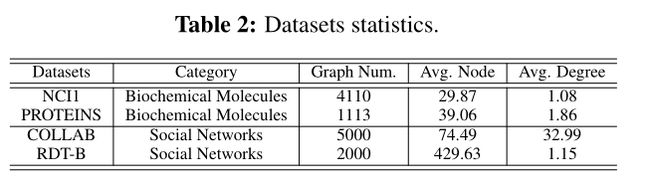
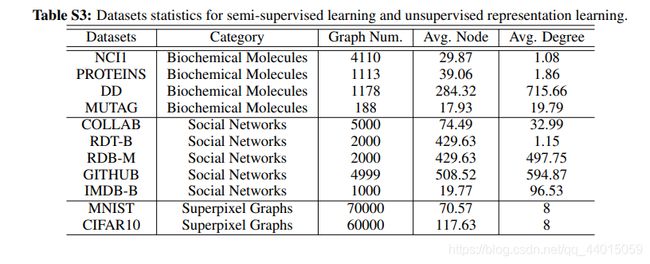
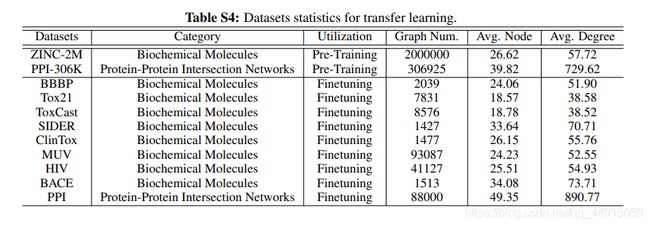
论文笔记：NIPS 2020 Graph Contrastive Learning with Augmentations

前言

本文主要提出在图对比学习大框架下的图数据增强的若干方法。

概括来说，本文提出了一种图对比学习框架来无监督的完成图表示学习，首先作者提出了基于各种先验信息的四种图数据增强方法。然后，作者分析了在四种不同的图数据增强条件下，不同组合对多个数据集的影响:半监督、无监督、迁移学习以及对抗性攻击。

作者为 GNN 的预训练提出了基于图数据增强的对比学习框架来解决图中数据异质性的挑战，本文的主要贡献如下：

1. 作者提出了四种图数据增强的方法，并且四种方法对图数据施加一定的先验性，并对范围和模式进行参数化。
2. 作者提出了一种新的用于 GNN 预训练的图对比学习框架 (GraphCL)，从而使模型具有对图结构数据噪音的抗干扰性，并且能够学习具体的特征表示。此外，GraphCL 实际上实现了交互信息最大化，GraphCL可以重写为一个通用框架，统一图结构数据上的一系列对比学习方法。

论文链接：https://arxiv.org/pdf/2010.13902.pdf
github：https://github.com/Shen-Lab/GraphCL

1. Related Work

1.1 Graph neural networks

令 $\mathcal{G}=\{\mathcal{V},\mathcal{E}\}$ 表示一个无向图，$\mathbf{X}\in {\mathbb{R}}^{|\mathcal{V}|\times N}$ 代表节点特征矩阵。对应于 $|\mathcal{V}|$ 代表图中节点个数，$N$ 代表特征维度。基于此对于一个 $K$-层的 GNN 信息传播函数 $f(\cdot )$，可以表示为如下的形式：
$$a_n^{(k)}=Aggregatio{n}^{(k)}(\{h_{n^{{}^{\prime }}}^{(k-1)}:n^{{}^{\prime }}\in \mathcal{N}(n)\}),h_n^{(k)}=Combin{e}^{(k)}(h_n^{(k-1)},a_n^{(k)})$$

其中 $h_n^{(k)}$ 代表节点 $n$ 在第 $k$ 层的嵌入，因此 $h_n^{(0)}=x_n$，$\mathcal{N}(n)$ 代表节点 $n$ 的邻接节点结合。$Aggregation(\cdot )$ 和 $Combine(\cdot )$ 是 GNN 层的组成函数，经过 $K$-层的传播之后，需要经过一个 $Readout(\cdot )$ 得到图中所有结点经过 GNN 的特征表示输出。举例来说，对于图级别的任务来说，多层感知机基于已经学习到的图特征对于特定的下游任务进行训练，下游任务可以是分类任务或者回归任务。对于上述过程可以表示为：
$$f(\mathcal{G})=Readout(\{h_n^{(k)}:v_n\in \mathcal{V},k\in K\}),z_G=MLP(f(\mathcal{G}))$$

1.2 Graph data augmentation

对于图结构数据的增强仍然没有得到充分的探索，一些工作沿着这些线进行，但需要额外计算成本。传统的自我训练方法利用训练后的模型对未标记数据进行标注，之前的方法提出在对抗学习设置中训练一个生成-分类器网络来生成假节点，一些方法对图结构上的节点特征产生对抗性扰动。

1.3 Pre-training GNNs

虽然预训练是卷积神经网络(convolutional neural networks, CNNs)的一种常用且有效的方案，但对GNNs的预训练研究却很少。作者认为，由于图结构数据来源的不同领域，预训练的 GNN 不容易迁移。在迁移过程中，预训练过程和下游任务都需要大量的领域先验信息，否则可能会导致负迁移。

1.4 Contrastive learning

对于图数据，传统方法试图重建结点的邻接矩阵，这种方法可以视为一种“局部对比”，但是过分强调邻近信息而牺牲了结构信息。之后的一些方法提出在局部和全局表示之间进行对比学习，以更好地捕捉结构信息。然而，图对比学习还没有从增强数据不变性的角度进行探讨。

2. Method

2.1 Data Augmentation for Graphs

数据增强的目的是在不影响语义标签的情况下，通过一定的变换来生成符合实际的数据用于后续的训练。在此篇文章中，作者主要提出的图数据增强方法是基于图级别来说的，因此图的定义为 $\mathcal{G}\in \{{\mathcal{G}}_m:m\in M\}$，其中 $M$ 代表数据集中共有 $M$ 张图。定义数据增强后生成的图数据为 $\hat{\mathcal{G}}\sim q(\hat{\mathcal{G}}|\mathcal{G})$，其中 $q(\cdot |\mathcal{G})$ 是以原始图为条件的增广分布，这是预先定义的，表示数据分布的先验信息。例如，在图像分类中，旋转和裁剪的应用对人们从旋转后的图像或其局部的 patch 中获得的基于分类的语义知识进行编码。

对于图数据的数据增强来说，不同类别的图数据集可能需要不同的数据增强方法，因为图的应用范围非常广泛，不同的图数据集可能代表完全不同的语义信息和不同的出发点，在这点上与图片信息形成了鲜明的对比。目前还没有一个统一的数据增强的方法可以适用于所有的图数据，作者主要基于生物化学分子图数据集、社交网络数据集、图像超分辨率图数据集进行试验并提出了四种普适的图结构数据增强方法：

1. Node dropping
   节点丢弃：给定图 $\mathcal{G}$，节点丢弃将随机丢弃部分顶点及其连接的边。它所强制的基础先验信息是，缺少部分顶点并不影响 $\mathcal{G}$ 的语义信息。同时每个节点的 drop 概率遵循默认的i.i.d.均匀分布(或任何其他分布)。

2. Edge perturbation
   边的干扰：通过随机增加或减少一定比例的边，会干扰 $\mathcal{G}$ 中的连通性。$\mathcal{G}$ 的语义信息对边拓扑结构的变化具有一定的鲁棒性。遵循默认的i.i.d.均匀分布(或任何其他分布)。增加/减少边。

3. Attribute masking
   属性屏蔽：属性屏蔽提示模型使用上下文信息恢复被屏蔽的节点属性，即剩余的属性。基本的假设是缺少部分顶点属性不会对模型预测产生很大影响。

4. Subgraph
   生成子图：举例来说使用随机漫步（random walk）从 $\mathcal{G}$ 中抽取了一个子图样本。它假设 $\mathcal{G}$ 的语义可以在其局部结构中得到很大程度的保留。

默认的增强(下降，扰动，掩蔽和子图)比例设置为0.2。

2.2 Graph Contrastive Learning

作者提出了一个用于 GNN (自我监督)预训练的图对比学习框架(GraphCL)。在图对比学习中，通过图1所示的潜在空间中的对比损失来最大化同一图的两个增强图之间的一致性，从而进行预训练。该框架由以下四个主要部分组成:

1. Graph data augmentation
   首先将原始图 $\mathcal{G}$ 经过图数据增强生成两个相关的增强后的图 $\widehat{{\mathcal{G}}_i}$ 和 $\widehat{{\mathcal{G}}_j}$。中间过程为 $\widehat{{\mathcal{G}}_i}\sim q_i(\cdot |\mathcal{G})$ 和 $\widehat{{\mathcal{G}}_j}\sim q_j(\cdot |\mathcal{G})$。作者上面提到了四种图增强策略，同时也说明不同的数据集可能包含不同的语义信息，由于模型框架只生成两种增强后的图，因此选择增强的策略需要具体分析。

2. GNN-based encoder
   一个基于 GNN 的编码器函数可以表示为 $f(\cdot )$，它可以用于提取整张图的特征表示，因此对于不同的增强图 $\widehat{{\mathcal{G}}_i}$ 和 $\widehat{{\mathcal{G}}_j}$ 可以得到 $h_j$ 和 $h_j$。图对比学习框架不受选择不同 GNN 编码函数的限制

3. Projection head
   一个名为投影头的非线性变换 $g(\cdot )$ 将特征表示映射到另一个计算对比损失的潜在空间。在图对比学习中，利用两层感知器(MLP)得到 $z_i$，$z_j$。

4. Contrastive loss function
   本文定义了一个对比损失函数 $\mathcal{L}(\cdot )$，使正数对 $z_i$，$z_j$ 与负数对的一致性最大化。作者使用归一化的温度度量的交叉熵损失函数（NT-Xent）

在GNN预训练过程中，随机抽取的 $N$ 个图，通过对比学习进行处理，得到 $2N$ 个增强图和相应的对比损失，从而进行优化，其中作者将 $z_i$，$z_j$ 重新标注为 $z_{n,i}$，$z_{n,j}$，作为 minibatch 中的第 $n$ 个图。负样本对不是显式采样的，而是由相同 minibatch 的其他 $N-1$ 增强图生成的。余弦相似函数可以表示为 $(z_{n,i},z_{n,j})=z_{n,i}^T{z}_{n,j}/||z_{n,i}||||z_{n,j}||$因此对于第 $n$ 个图的损失函数可以定义如下：
$$l_n=-log\frac{exp(sim(z_{n,i},z_{n,j})/\mathcal{T})}{{\sum }_{n^{{}^{\prime }}=1,n^{{}^{\prime }}\ne n}^{N}exp(sim(z_{n,i},z_{n,j})/\mathcal{T})}$$

其中 $\mathcal{T}$ 代表温度度量的超参数，在 minibatch 中计算所有正对的最终损失。作者证明了GraphCL 可以被看作是两类增强图潜在表示之间的互信息最大化的一种方法。对应于此，损失函数可以表示成如下形式：
$$l={\mathbb{E}}_{{\mathbb{P}}_{\widehat{{\mathcal{G}}_i}}}\{-{\mathbb{E}}_{{\mathbb{P}}_{(\widehat{{\mathcal{G}}_j}|\widehat{{\mathcal{G}}_i})}}T(f_1(\widehat{{\mathcal{G}}_i}),f_2(\widehat{{\mathcal{G}}_j}))+log({\mathbb{E}}_{{\mathbb{P}}_{\widehat{{\mathcal{G}}_j}}}{e}^{T(f_1(\widehat{{\mathcal{G}}_i}),f_2(\widehat{{\mathcal{G}}_i}))})\}$$

上述损失本质上是使互信息 $(f_1(\widehat{{\mathcal{G}}_i})$ 和 $(f_2(\widehat{{\mathcal{G}}_j})$ 之间的一个下界最大化。其中 $(f_1，\widehat{{\mathcal{G}}_i})$ 和 $(f_2,\widehat{{\mathcal{G}}_j})$ 决定了具体的数据增强方法和 GNN 信息传播方法

3. Experiments

GraphCL框架中图的数据增强作用。如图所示，以半监督人物为例，横轴、纵轴分别表示框架图中的两个增强方式的具体实施方案，其中Identical表示原图数据，不同的数值变化表示相比于与baseline之间的精度波动。


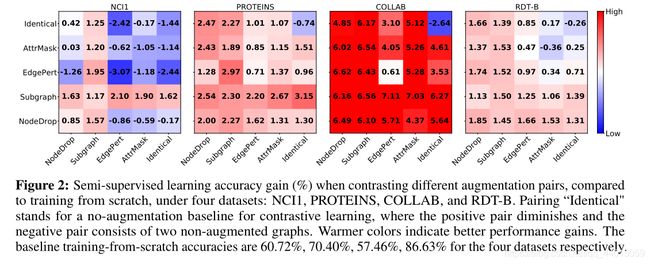
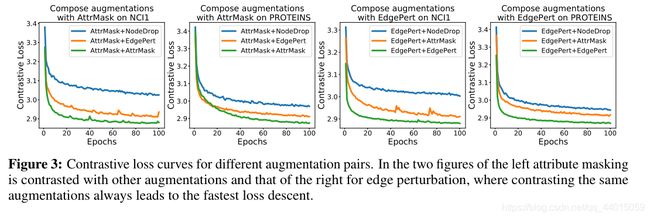
通过实验数据可以得到如下结论：

1. 数据扩充对图对比学习至关重要。当应用适当的扩充时，会灌输数据分布上的相应先验，从而通过最大化图及其扩充之间的一致性来使模型学习对所需扰动不变的表示。
2. 组合不同的扩充方式会带来更多的性能收益。与图中对角线的增益相比，最优的增益往往在应用不同的数据扩充方式进行对比学习时获得。这点在视觉对比学习任务中也有类似的结论，组合不同的扩充方式会避免学习到的特征过于拟合low-level的"shortcut"，从而使得特征更加的具有通用性。此外，训练不同的特征之间的对比学习模型会使得收敛速度下降。

作者研究的生物分子图数据集、社交网络图数据集、图像超分辨率图数据集进行具体分析
作者进行了相应的实验，结论如下：

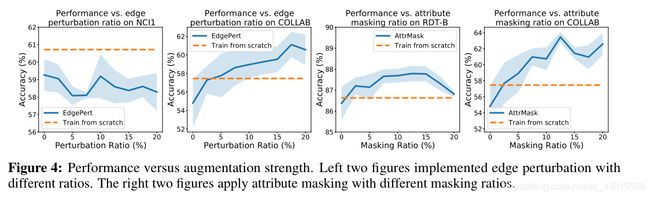
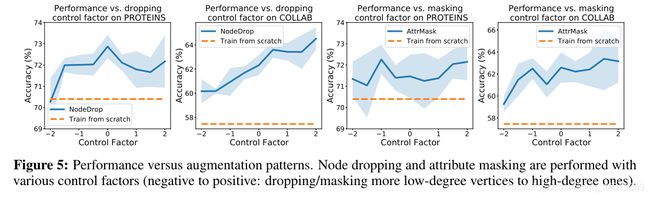
1. 边缘扰动有益于社交网络，但会伤害一些生化分子图。这取决于边的重要程度（图4左2）。
2. 应用属性屏蔽可在更密集的图中实现更好的性能（图4右2）。

3. 节点删除和子图通常对图数据集有益。节点删除在丢失某些顶点不会更改语义信息的先验条件下直观的迎合了我们的认知。子图刻意增强局部（即子图）和全局信息的一致性有助于表示学习。

4. 对于过于简单的图学习任务，对比学习的效果不显著。

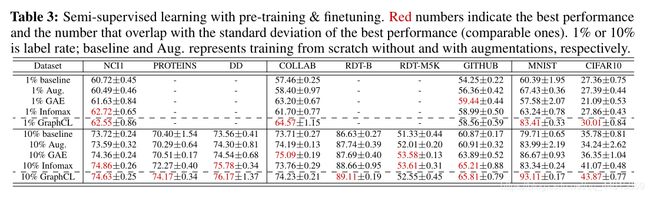
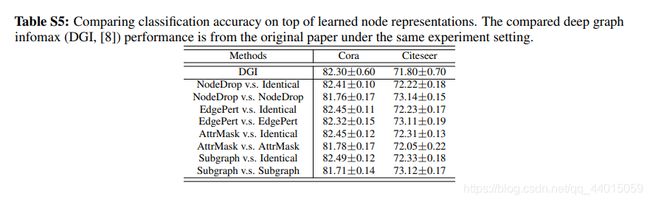
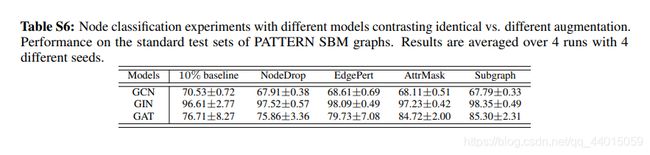
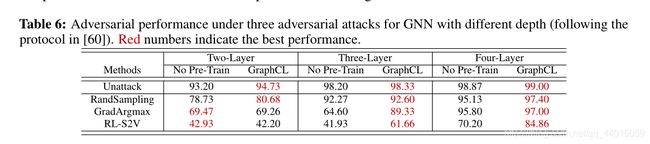
实验效果：

1. 半监督学习任务
   
2. 弱监督
   
   
3. 迁移学习
   
4. 对抗鲁棒性测试