C语言从入门到入土——操作符超详细总结

个人主页：泡泡牛奶

系列专栏：C语言从入门到入土

本章节将会给大家带来最详细的操作符大总结，全是干货绝无尿点如果想了解更多有关C语言的内容，就关注我的专栏吧，相信你一定能从中学到很多有意思的知识

操作符有哪些？

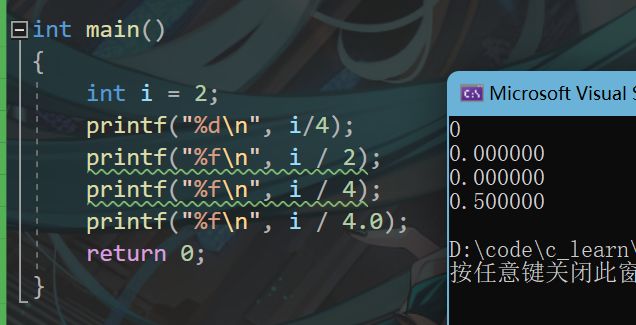
1. 算数操作符

  +   -   *   /    %
  加  减  乘   除   模（取余数）

注意：

1. 只有 % 不能进行浮点数的计算，其余都可以（ % 计算的是余数，所以操作数必须为整数）
2. 如果 / 两边的操作数都为整型，则结果也为整型；如果 / 两边操作数至少有一个为浮点型的数，结果则为浮点型。

2. 移位操作符

<<   左移操作符
>>   右移操作符

注意： 移位操作符的对象只能是 整数

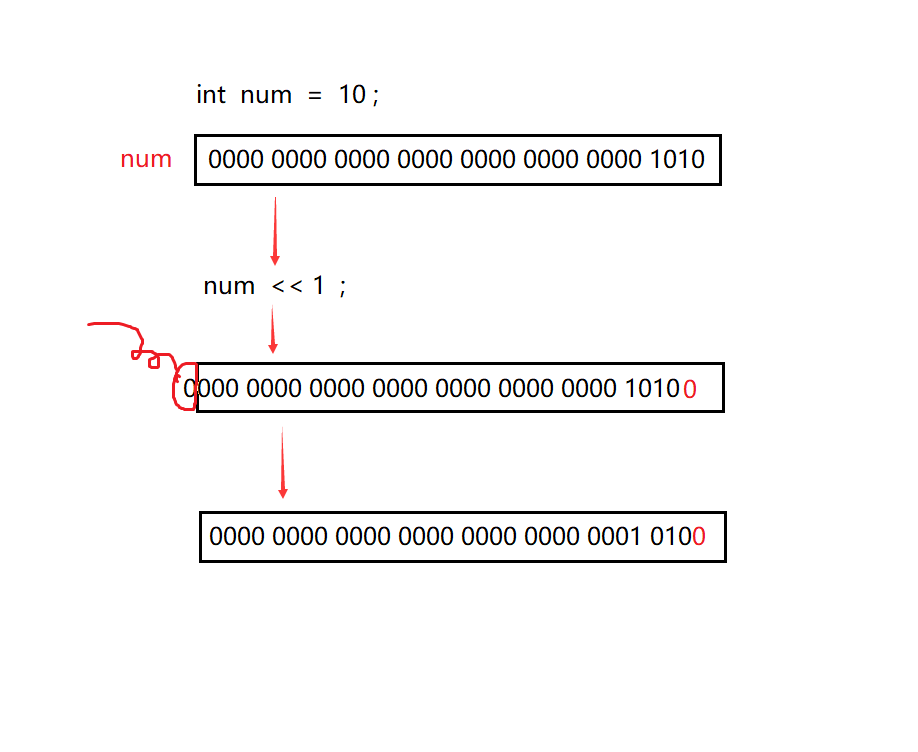
2.1 左移操作符

移位规则：

左边抛弃，右边补0

理论存在，那个操作符可以方便我们做什么呢？

请看下面一串代码：

#include 

int main()
{
	int num = 1;
	int i = 0;
	for (i = 0; i <= 10; ++i)
	{
        //num 左移 i 位
		printf("%d ", num << i);
	}
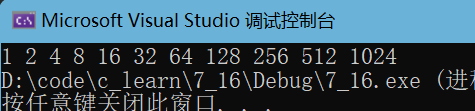
	return 0;
}

输出结果为：

可以看到，每次移位，都是2的倍数，试将 num 改成不同的数字，可以发现，结果都保持一个规律 —— $$n\ast 2^i$$

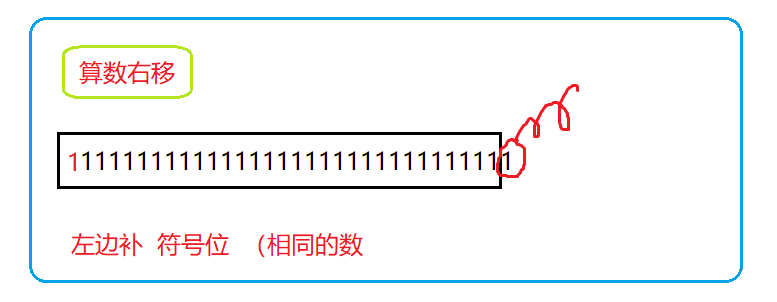
2.2 右移操作符

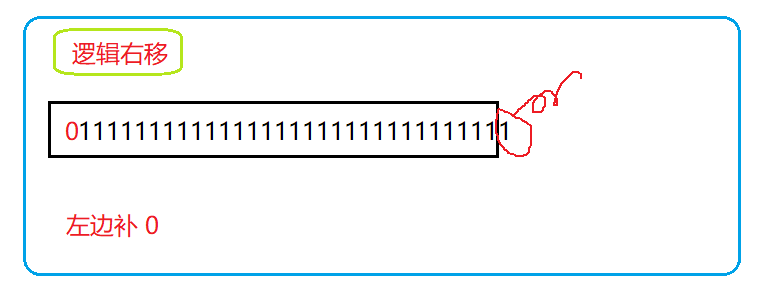
移位规则：

1. 逻辑移位：左边用 0 填充， 右边丢弃

2. 算数位移：左边用 符号位 填充，右边丢弃

注意：

• 对于右移操作符，逻辑右移 和 算数右移 通常由 编译器决定_{(但大多都是算数右移，VS就是算数右移)}
• 对于移位运算符，不要移动负数位，这属于C语言标准未定义的

例如：

int num = 10;
num >> -1; //error

3. 位操作符

&   按位与      遇0则0
|   按位或      遇1则1
^   按位异或    相同为1,相异为0

注意： 位操作符的对象只能是 整数

既然知道了位操作符的基本原理，那么就来练习一下吧

练习1：

在不创建临时变量的情况下（第三个变量），交换两个数的值

#include 

int main()
{
    int a = 10;
    int b = 20;
    a = a^b;
    b = a^b;
    a = a^b;
    printf("a = %d , b = %d\n", a, b);
    return 0;
}

练习2：

求一个整数在内存中的二进制 1 的个数

#include 
int main()
{
	int num = 10;
	int count = 0;//计数
	while (num)
	{
		if (num % 2 == 1)
			count++;
		num = num / 2;
	}
	printf("%d\n", count);
	return 0;
}

可以思考以下这样是否可行？

当 num 为正数的时候，这样的方法显然是可行的，但是当 num 为负数的时候，再进行取余就不正确了。

那么我们应该怎样写呢？

//方法2
#include 
int main()
{
	int num = -1;
	int i = 0;
	int count = 0;//计数
	for (i = 0; i < 32; i++)
	{
		if (num & (1 << i))
			count++;
	}
	printf("二进制中1的个数 = %d\n", count);
	return 0;
}

对于这样的代码显然已经达到了我们所要的目的，但是，能否对这样的代码进行优化呢？这样的代码无论如何都要进行32次。

#include 
int main()
{
	int num = -1;
	int i = 0;
	int count = 0;//计数
	while (num)
	{
		count++;
		num = num & (num - 1);
	}
	printf("%d\n", count);
	return 0;
}

思路：

num & ( num - 1 ) 会比原来的二进制位1的个数少1

4. 赋值操作符

=
    
复合赋值符号
+=
-=
*=
/=
%=
>>=
<<=
&=
|=
^=

使用时请注意符号优先级，赋值操作符优先级较低，且是右结合性，会首先计算右边的数，最后赋值给左边。例如：

int a = 10;
int x = 1;

x += a += a + x;

计算步骤
        10   10  1
1.  a = a + (a + x);
//此时  a = 21
	    1   21
2.  x = x + a;

3. x = 22;

注意：

上面这样写，是不好的，这样不利于调试

最好是分开写，有利于调试，如下：

int a = 10;
int x = 1;

a += a + x;
x += a;

5. 单目操作符

!     	逻辑取反
-		负值
+		正值（一般不会用到）
&		取地址
sizeof	计算操作数的类型长度（以字节为单位）
~		按（二进制）位取反
--		前置、后置--
++		前置、后置++
*		间接访问操作符（解引用操作符）指针会用
(类型)   强制类型转换

何为单目操作符呢？

• 单目操作符就是，只有一个操作数的操作符

  而 a + b 是双目操作符 ，请区别于 -a

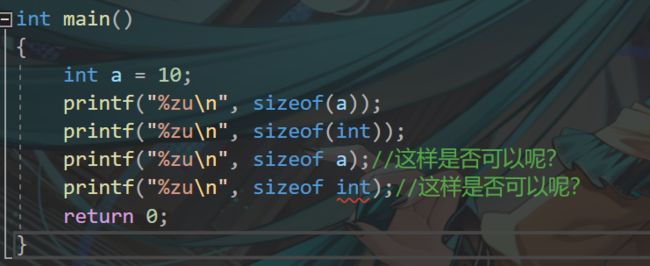
这里我们可以看到 sizeof 竟然是一个操作符？？该怎样证明它是一个操作符呢？

#include 

int main()
{
    int a = 10;
    printf("%zu\n", sizeof(a));
    printf("%zu\n", sizeof(int));
    printf("%zu\n", sizeof a);//这样是否可以呢？
    printf("%zu\n", sizeof int);//这样是否可以呢？
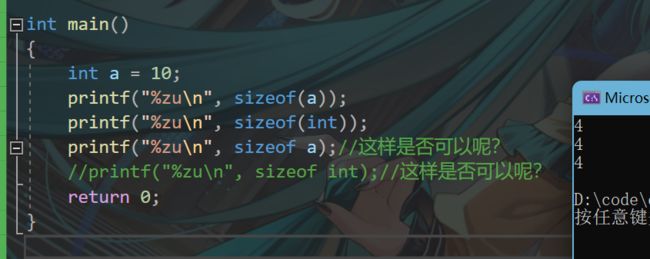
    return 0;
}

可以看到， sizeof int 发生了错误，那把它注释掉再来运行看看

我们发现第 1、2、3 种写法都可以计算大小，对比函数，函数不能直接传入类型，且调用时必须要加上 () ，综上，我们可以得出 sizeof 不是函数，而是操作符。

6. 关系操作符

>
>=
<
<=
!=		用于判断“不相等”
==		用于判断“相等”

注意在写的过程中不要把 == 写成了 = ，== 是判断相等的， = 是赋值的

7. 逻辑操作符

&&		逻辑与（并且）
||		逻辑或（或者）

区别逻辑与和按位与

区别逻辑或和按位或

1&2  --->   0
1&&2 --->   1

1|2  --->   3
1||2 --->   1

逻辑与和逻辑或的特点：

逻辑与：当表达式从左向右，遇到 假（ 0 ）的时候，表达式停止继续读取

逻辑或 ：当表达式从左向右，遇到 真（ 非0 ）的时候，表达式停止继续读取

例如：

#include 

int main()
{
    int i = 0,a=0,b=2,c =3,d=4;
	i = a++ && ++b && d++;   //1
	//i = a++||++b||d++;     //2
	printf("a = %d\n b = %d\n c = %d\nd = %d\n", a, b, c, d);
    return 0;
}

8. 条件操作符

exp1 ? exp2 : exp3

可以等同于

if (exp1)
{
    exp2;
}
else
{
    exp3;
}

9. 逗号表达式

exp1,exp2,exp3,……,expN

逗号表达式，就是用都好隔开的多个表达式。

逗号表达式，从左到右依次执行，表达式最后的结果是最后一个表达式的结果。

例如：

int c = (1,2,3,4,5);

c会被赋值成5

10. 下标引用、函数调用和结构成员

1. 下标引用操作符 [ ]

操作数 ： 数组名 + 一个索引值

int arr[10];
arr   [   9   ]   =   10  ；
数组名   索引值
[   ]   的两个操作数是 arr 和  9

2. 函数调用操作符 ( )

可以接受一个或者多个操作数 ： 第一个为函数名， 其余作为参数传递给函数

#include 

void test(const char* str)
{
    printf("%s\n", str);
}

int main()
{
    test("hello world");
    return 0;
}

3. 访问一个结构体成员

. 结构体 . 成员名

-> 结构体 -> 成员名

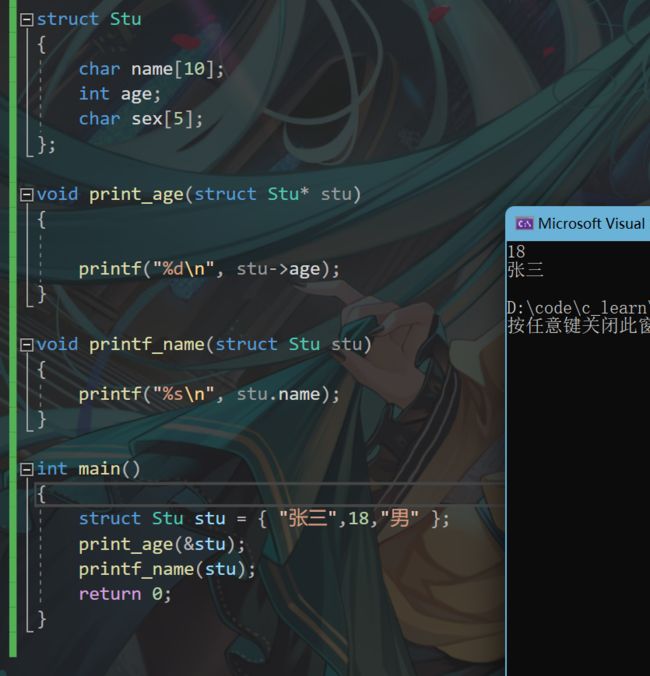
例如：

#include 

struct Stu
{
	char name[10];
    int age;
    char sex[5];
};

void print_age(struct Stu* stu)
{
    
    printf("%d\n", stu->age);
}

void printf_name(struct Stu stu)
{
    printf("%s\n", stu.name);
}

int main()
{
    struct Stu stu = { "张三",18,"男" };
    print_age(&stu);
    printf_name(stu);
    return 0;
}

效果如图：

11. 表达式求值

操作符主要是为了方便我们可以进行更好的计算表达式的值。

而在计算时，主要根据操作符的优先级和结合性进行计算。

操作符	描述	用法示例	结合性	是否控制求值顺序
( )	聚组	(表达式)	/	否
( )	函数调用	f (rexp1, rexp2, … )	从左到右	否
[ ]	下标引用	数组名[下标]	从左到右	否
.	访问结构成员	rexp.member_name	从左到右	否
->	访问结构指针成员	rexp->member_name	从左到右	否
++	后置自增	exp++	从左到右	否
–	后置自减	exp–	从左到右	否
!	逻辑反	! exp	从右到左	否
~	按位取反	~ exp	从右到左	否
+	单目，表示正值	+ exp	从右到左	否
-	单目，表示负值	- exp	从右到左	否
++	前置自增	++ exp	从右到左	否
–	前置自减	– exp	从右到左	否
*	间接访问	* exp	从右到左	否
&	取地址	& exp	从右到左	否
sizeof	计算字节大小	sizeof exp \ sizeof (类型)	从右到左	否
(类型)	强制类型转换	(类型) rexp	从右到左	否
*	乘法	exp * exp	从左到右	否
/	除法	exp / exp	从左到右	否
%	整数取余	exp % exp	从左到右	否
+	加法	exp + exp	从左到右	否
-	减法	exp - exp	从左到右	否
<<	左移位	rexp << rexp	从左到右	否
>>	右移位	rexp >> rexp	从左到右	否
>	大于	exp > exp	从左到右	否
>=	大于等于	exp >= exp	从左到右	否
<	小于	exp < exp	从左到右	否
<=	小于等于	exp <=exp	从左到右	否
==	等于	exp == exp	从左到右	否
!=	不等于	exp != exp	从左到右	否
&	按位与	exp & exp	从左到右	否
^	按位异或	exp ^ exp	从左到右	否
|	按位或	exp | exp	从左到右	否
&&	逻辑与	exp && exp	从左到右	是
||	逻辑或	exp || exp	从左到右	是
? :	条件操作符	exp1 ? exp2 : exp3	/	是
=	赋值	变量 = 表达式	从右到左	否
+=	加后赋值	变量 += 表达式	从右到左	否
-=	减后赋值	变量 -= 表达式	从右到左	否
*=	乘后赋值	变量 *= 表达式	从右到左	否
/=	除后赋值	变量 /= 表达式	从右到左	否
%=	取模后赋值	变量 %= 表达式	从右到左	否
<<=	左移后赋值	变量 <<= 表达式	从右到左	否
>>=	右移后赋值	变量 >>= 表达式	从右到左	否
&=	按位与后赋值	变量 &= 表达式	从右到左	否
^=	按位异或后赋值	变量 ^= 表达式	从右到左	否
|=	按位或后赋值	变量 |= 表达式	从右到左	否
,	逗号	表达式1，表达式2，……	从左到右	是

小记：

后置加减 > ! (逻辑反) > 算数运算符 > 逻辑运算符 > 按位 & ^ | > && > || > 赋值运算符

11.1 隐式类型转换

可以思考以下，为什么隐式类型转换要叫隐式类型转换呢？

隐式类型转换就是在进行算数运算时，发生的一些我们无法观察到的偷偷的进行的转化。

例如：C语言在进行整型算数运算时，为了获得更高的精度，从而将一些字符型或者短整型转化成普通整进行计算，这种转换称之为整型提升。而整型提升是按符号位来进行提升。

例如

char c1 = 1;
补码：
    0000 0001
整型提升 —— 符号位是 0
    0000 0000 0000 0000 0000 0000 0000 0001

char c2 = -1;
补码：
	1111 1111
整型提升 —— 符号位是 1
    1111 1111 1111 1111 1111 1111 1111 1111

那么是如何进行隐式类型转换的呢？_{（以整型来举例）}

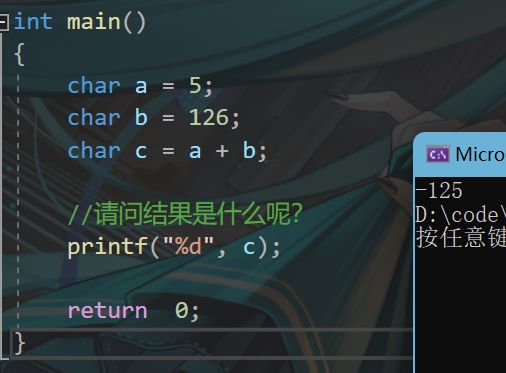
请看下面的例子

int main()
{
    char a = 5;
	char b = 126;
	char c = a + b;
    
    //请问结果是什么呢？
    printf("%d", c);
    
    return  0;
}

char a = 5;
源反补相同
补码：
    0000 0101

char b = 126;
补码：
	0111 1110

char c = a + b;
a进行整型提升
    0000 0000 0000 0000 0000 0000 0000 0101
b进行整型提升
    0000 0000 0000 0000 0000 0000 0111 1110
c = a + b;
	0000 0000 0000 0000 0000 0000 1000 0011
因为c是 (unsigned)char 类型，进行截断
    1000 0011  -  c
需要以整型的形式打印，进行整型提升，最高位是1，判断是负数
    1111 1111 1111 1111 1111 1111 1000 0011  -  补码
    1111 1111 1111 1111 1111 1111 1000 0010  -  反码
    1000 0000 0000 0000 0000 0000 0111 1101  -  源码
结果打印
    -125

例2：

int main()
{
	char c = 1;
	printf("%zu\n", sizeof(c));//?
	printf("%zu\n", sizeof(+c));//?
	printf("%zu\n", sizeof(-c));//?
	return 0;
}

原因：

• 第二、三字节大小为4，是因为作为表达式进行了整型提升

11.2 算数转换

这里我们会有个疑问，当我的表达式计算超过一个整型大小的时候又该怎么办呢？

当一个表达式中出现多个类型的表达式时，计算会发生算数转换，具体会按照下面的方式由下往上转换。最终转换为最大的类型计算

long double
double
float
unsigned long int
long int
unsigned int
int
short/char

注意：

就算我们掌握了操作符的优先级和结合性，并不是说我们能对任何一种表达式都能计算出唯一的结果。

例如：

//表达式1
a*b + c*d + e*f;
计算顺序可能是：
    1. a*b
    2. c*d
    3. a*b + c*d
    4. e*f
    5. a*b + c*d + e*f
也有可能是：
    1. a*b
    2. c*d
    3. e*f
    4. a*b + c*d
    5. a*b + c*d + e*f

大家光这样看可能无法直接看出这样的危害，那我们换一种：

//表达式2
c + --c;

操作符的优先级只能决定 自减 -- 的运算在 + 运算的前面，但我们并不知道，+ 操作符的 左操作数 的获取在 右操作数 之前还是之后，所以结果不可预知。

//代码3
int fun()
{
	static int count = 1;
	return ++count;
}
int main()
{
	int answer;
	answer = fun() - fun() * fun();
	printf( "%d\n", answer);//？
	return 0;
}

上面的代码 answer = fun() - fun() * fun() 由优先级可知：先算乘法，再算减法，但是函数调用的优先级更高 ，因此无法判断先调用哪一对，count该计算哪一次的值。

小结：

我们写出的表达式如果不能确定唯一的计算路径，那么这个表达式就是存在问题的。

---

好啦，本章的内容到这里就结束，如果对你有那么一丝丝帮助的话，还不忘点个赞，如果你怕忘记里面的内容也可以先收藏起来，方便要看的时候随时都可以看啦