C++寒假班错题集（1.29）
错题题目
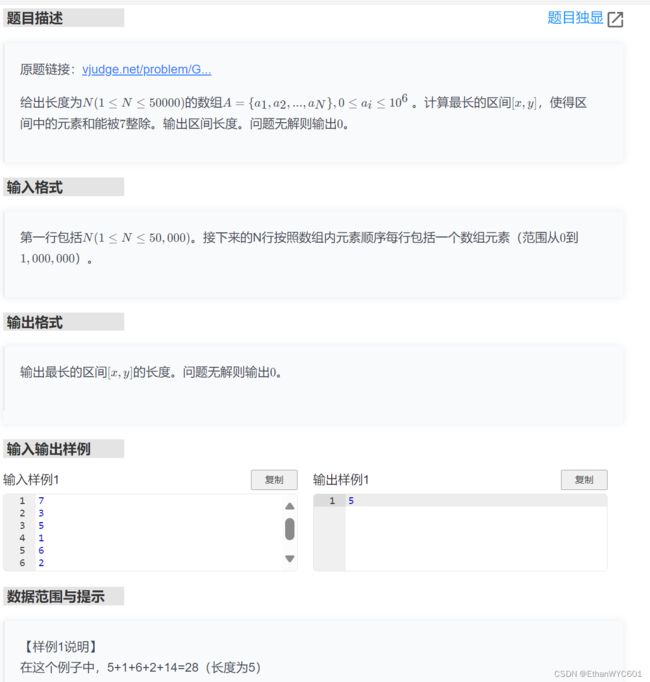
1.Restaurant Customers
2.[USACO16JAN] Subsequences Summing to Sevens S
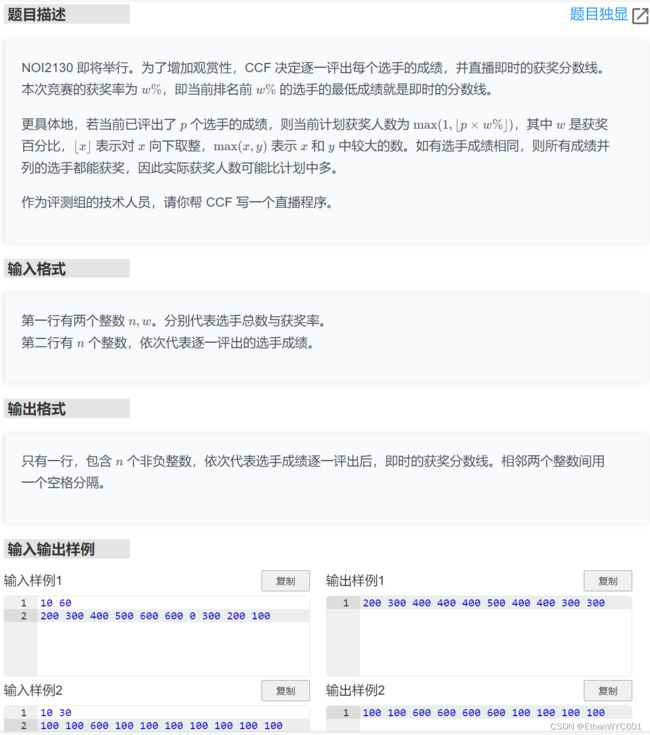
3.直播获奖
Restaurant Customers 
重点看一下数据范围
如果暴力枚举b - a每次把人数加一,
那么最坏情况下a=1,b=10^9 时间复杂度是ʘ(n·(b-a)),那就约是10^9 * 2 * 10^5，那一定时间超，统计的内存也超
错误示范，勿效仿只能的得44分
在这里我们不需要每个都统计一下前缀和，什么是前缀和呢？
就是每个时间点的顾客人数
我们来看一下解题思路：
从这里面，我们接可以延伸出他们的代码写法，首先创建一个数组表示是来是去，例如一个顾客从3点来6点走，我们可以表示为3 1，6 -1，3点顾客数+1，6点又走了一个顾客，所以顾客数-1。
然后按时间排序，统计前缀和最大的那一个。
来看一下代码
#include
using namespace std;
int main() {
ios::sync_with_stdio(false), cin.tie(0);
int n;
cin >> n;
vector> A; // 存放所有客户事件
for (int i = 0, l, r; i < n; i++) // 到达&离开事件
cin >> l >> r, A.push_back({l, 1}), A.push_back({r, -1});
sort(begin(A), end(A)); // 按时间排序
int s = 0, ans = 0;
for (auto p : A)
s += p[1], ans = max(ans, s); // 更新当前客户数以及历史客户数最大值
return printf("%d\n", ans), 0;
} 在这里用array(STL 中的数组，第一个表示typename,第二个表示范围)是因为array自动用第一个排序，pair也一样。
这里第一天就讲完了
[USACO16JAN] Subsequences Summing to Sevens S
看一下题目
这里不会超时,所以暴力枚举就可以了。
我们来看一下这里的解题思路
代码逻辑很简单
#include
using namespace std;
const int MOD = 7;
int main() {
int N;
cin >> N;
int ans = 0;
vector F(MOD, -1);
F[0] = 0;
for (int i = 1, a, s = 0; i <= N; i++) {
cin >> a, (s += a) %= MOD; //先加a再取模
//第一个余数记下来，见过的就计算这个区间长度
F[s] == -1 ? (F[s] = i) : (ans = max(ans, i - F[s]));
}
cout << ans << '\n';
} 直播获奖
这个题目的逻辑很好理解吧，给你一堆数据排个序按照他的要求输出。
但看了这个测试点我就懵了这个数也太大了吧！
排序就i就涉及了一个知识，他说满分只有600所以可以用计数排序，啥意思呢？
计数排序使用一个额外的数组C，其中第i个元素是待排序数组A中值等于i的元素的个数。
计数排序的核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。作为一种线性时间复杂度的排序，计数排序要求输入的数据必须是有确定范围的整数。
——知乎
这玩意就太生涩了理解一下，就是把每个数出现了多少遍标记来，输出这个数时多输出这么多遍。好理解了吧。
我们来看一下代码：
#include
using namespace std;
const int SS = 600;
int B[SS + 4]; // B[i]: 分数i的出现次数
int solve(int cnt, int w) {
int line = max(1, cnt * w / 100);
for (int j = SS, c = 0; j >= 0; j--)
if ((c += B[j]) >= line) return j; // 分数j之上刚好人数够了
return -1;
}
int main() {
ios::sync_with_stdio(false), cin.tie(0);
int n, w; cin >> n >> w;
fill_n(B, SS, 0);
for (int i = 1, x; i <= n; i++)
cin >> x, B[x]++, printf("%d ", solve(i, w));
puts("");
return 0;
} 谢谢。