HiveSQL——共同使用ip的用户检测问题【自关联问题】

注：参考文章：

SQL 之共同使用ip用户检测问题【自关联问题】-HQL面试题48【拼多多面试题】_hive sql 自关联-CSDN博客文章浏览阅读810次。0 问题描述create table log( uid char(10), ip char(15), time timestamp);insert into log valuesinsert into log values('a', '124', '2019-08-07 12:0:0'),('a', '124', '2019-08-07 13:0:0'),('b', '124', '2019-08-08 12:0:0'),('c', '124', '2019-0._hive sql 自关联https://blog.csdn.net/godlovedaniel/article/details/119858751

0 问题描述

1 数据准备

create table log
(
  uid string,
  ip string,
  login_time string
)row format delimited
fields terminated by '\t';
 
insert into log values
('a', '124', '2019-08-07 12:00:00'),
('a', '124', '2019-08-07 13:00:00'),
('b', '124', '2019-08-08 12:00:00'),
('c', '124', '2019-08-09 12:00:00'),
('a', '174', '2019-08-10 12:00:00'),
('b', '174', '2019-08-11 12:00:00'),
('a', '194', '2019-08-12 12:00:00'),
('b', '194', '2019-08-13 13:00:00'),
('c', '174', '2019-08-14 12:00:00'),
('c', '194', '2019-08-15 12:00:00');

2 数据分析

   共同使用问题，一般此类题型都需要一对多，该问题的解决核心逻辑是自关联。

 完整代码如下：

select
   t3.uid_1, t3.uid_2
from (select
          t1.ip,
          t1.uid as uid_1,
          t2.uid as uid_2
      from (select uid, ip from log group by uid, ip) t1
               join
               (select uid, ip from log group by uid, ip) t2
      where t1.ip = t2.ip
        and t1.uid < t2.uid) t3
group by t3.uid_1, t3.uid_2
having count(ip) >= 3;

代码分析：

step1: 获取自关联的结果集

select
    t1.ip,
    t1.uid as uid_1,
    t2.uid as uid_2
from (select uid, ip from log group by uid, ip) t1
 join(select uid, ip from log group by uid, ip) t2
 on t1.ip = t2.ip;

step2: 由于数据会两两出现，所以a,b和 b,a实际上是一样的，需要过滤掉这部分重复数据，只需要选出 t1.uid < t2.uid，即过滤掉a,b这组数据。hive中不支持不等连接，故使用where语句

select
      t1.ip,
      t1.uid as uid_1,
      t2.uid as uid_2
from (select uid, ip from log group by uid, ip) t1
 join (select uid, ip from log group by uid, ip) t2
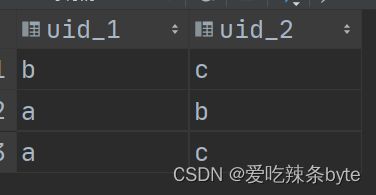
 where t1.ip = t2.ip and t1.uid < t2.uid;

step3:按照组合键分组，并过滤出符合条件的用户

select
   t3.uid_1, t3.uid_2
from (select
          t1.ip,
          t1.uid as uid_1,
          t2.uid as uid_2
      from (select uid, ip from log group by uid, ip) t1
               join
               (select uid, ip from log group by uid, ip) t2
      where t1.ip = t2.ip
        and t1.uid < t2.uid) t3
group by t3.uid_1, t3.uid_2
having count(ip) >= 3;

3 小结

    本案例题型属于：“共同xx”，例如：共同好友、互相认识、共同使用等。遇到这类关键字的时候，往往可以采用自关联的方式解决。（笛卡尔积：一对多；去重取一）