快速排序的多种实现方式----C语言数据结构
目录
-
- 引言
- 1.快排的递归实现
-
- hoare版本
- 挖坑法
- 前后指针法
- 2.快排的非递归实现
- 3.快排的时间复杂度分析
- **总结**
引言
快速排序（QuickSort）是一种基于分治法的排序算法，由英国计算机科学家 Tony Hoare 在1960年提出。它是一种高效的排序算法，在实际应用中被广泛使用。以下是快速排序的基本应用和创造者的相关信息：
基本应用：
-
排序： 快速排序是一种非常高效的排序算法，通常在需要对大量数据进行排序时使用。它的平均时间复杂度为 O(n logn)，这使得它比一些其他排序算法更快。
-
搜索： 快速排序的思想也可以应用于搜索算法，例如在有序数组中进行二分查找。
-
中位数查找： 快速排序的分治思想可以用于查找一组数据的中位数。
-
文件压缩： 快速排序的分区过程也可以用于文件压缩算法，例如 Huffman 编码。
创造者：
快速排序由英国计算机科学家 Tony Hoare 在1960年首次提出。Tony Hoare是计算机科学领域的重要人物，他还在并发计算、形式化方法等领域做出了许多贡献。快速排序的提出是他在ALGOL编程语言的背景下完成的。
1.快排的递归实现
hoare版本
实现的基本思路:
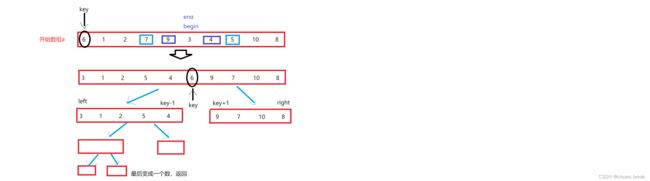
快排的递归思想是,先单趟,以开始元素为key,从右边开始找比key小的,从左边找比key大的,然后交换.当比key小的都在左边,比key大的都在右边,将key放到中间(介于他们的大小中间),然后左递归,右递归.直到完全有序
步骤;
- 先定义key,begin(左坐标),end(右坐标)
- 单趟循环,右找小,左找大(这里为什么要先右找下,而后左找大,是因为之后,把key值交换到中间,可以保证交换后a[key]值是一定会大于左边而小于右边的
) - 将key的左区间进行左递归,右区间进行右递归//[left,key-1]key[key+1,right]
- 最后使每个区间只有一个数,也就为绝对有序,整个数组便是有序了
单趟逻辑
递归逻辑
初版快排
void QuickSort1(int* a, int left, int right)
{
//如果区间只有一个数，或区间不存在
if (left >= right)
return;
//一个为左变量，一个为右变量
int begin = left , end = right;
int key = left;
//key为数组的开始
while (begin < end)
{
//先处理单趟，1.右找小
while (a[end] >= a[key]&&begin<end)//在比较的同时，需保证begin始终小于end
{
end--;
}
//2.左找大
while (a[begin] <= a[key]&&begin<end)
{
begin++;
}
Swap(&a[begin], &a[end]);
}
//将key交换至a[begin]
Swap(&a[key], &a[begin]);
key = begin;
//[left,key-1]key[key+1,right]
QuickSort1(a, left, key - 1);
QuickSort1(a, key + 1, right);
}
上一个版本在数据有一定的顺序时,相较于其他的堆排序,希尔排序,反而显得效率较低(比如,当一个数据只有2个数据是无序的,那么此时便会开出相较于无序数据的更多栈空间,而导致效率较低),所以针对更广的适用范围,优化每次取key的位置,使递归更能充分的利用
优化版快排
//找出begin,end和mid之间的中位数
int Getmid(int* a, int left, int right)
{
int mid = (left + right) / 2;
if (a[mid] > a[left])
{
if (a[mid] < a[right])
return mid;
else
if (a[left] > a[right])
return right;
else
return left;
}
else //a[mid]<=a[left]
{
if (a[mid] > a[right])
return mid;
else
if (a[right] > a[left])
return left;
else
return right;
}
}
int PartSort1(int* a, int left, int right)
{
int mid = Getmid(a, left, right);
Swap(&a[left], &a[mid]);
int begin = left, end = right;
int key = left;
while (begin<end)
{
//先处理单趟，1.右找小
while(a[end] >=a[key]&&begin<end)
{
end--;
}
//2.左找大
while (a[begin] <=a[key]&&begin<end)
{
begin++;
}
Swap(&a[begin], &a[end]);
}
//将key交换至a[begin]
Swap(&a[key], &a[begin]);
key = begin;
return key;
}
void QuickSort(int* a, int left, int right)
{
if (left >= right)
return;
int key = PartSort1(a, left, right);
QuickSort(a, left, key - 1);
QuickSort(a, key+1, right);
}
挖坑法
实现的核心思路还是和之前是一样的,而不同的是逻辑更能容易理解
先将a[left]放入key,坑位就挖好了,然后单趟遍历比较,最后key将坑位填上
int PartSort2(int* a, int left, int right)
{
int mid = Getmid(a, left, right);
Swap(&a[left], &a[mid]);
int key = a[left], begin = left, end = right;
int hole = left;
while (begin < end)
{
//先处理单趟，1.右找小
while (a[end] >= key && begin < end)
{
end--;
}
a[hole] = a[end];
hole = end;
//2.左找大
while (a[begin] <= key && begin < end)
{
begin++;
}
a[hole] = a[begin];
hole = begin;
}
a[hole] = key;
return hole;
}
void QuickSort(int* a, int left, int right)
{
if (left >= right)
return;
//int key = PartSort1(a, left, right);
int key = PartSort2(a, left, right);
QuickSort(a, left, key - 1);
QuickSort(a, key+1, right);
}
前后指针法
前后指针也就是快慢指针的思想:
- 快指针(下标)找比key小的值,当找到了,停下
- 慢指针不用找,只有在快指针将比key小的值与慢指针的位置交换时才走
- 单趟比较结束,将key的放到慢指针的位置,实现左右递归
单趟逻辑
// 快速排序前后指针法
int PartSort3(int* a, int left, int right)
{
int mid = Getmid(a, left, right);
Swap(&a[mid], &a[left]);
int key = left, prev = left, cur = left + 1;
while (cur <= right)
{
//if (a[key] >= a[cur])
//{
// prev++;
// Swap(&a[prev], &a[cur]);
//}
if (a[key] >= a[cur] && ++prev != cur)
{
Swap(&a[prev], &a[cur]);
}
cur++;
}
Swap(&a[key], &a[prev]);
key = prev;
return key;
}
void QuickSort(int* a, int left, int right)
{
if (left >= right)
return;
//int key = PartSort1(a, left, right);
//int key = PartSort2(a, left, right);
int key = PartSort3(a, left, right);
QuickSort(a, left, key - 1);
QuickSort(a, key+1, right);
}
2.快排的非递归实现
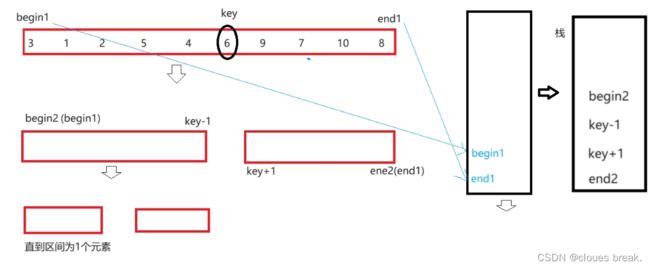
快排的非递归实现,实质是将递归的思想以循环来实现
可以用栈来辅助实现,将递归的过程转变成循环
- 先将数组的left,和right压栈,右先入栈,后左入栈
- 循环内,begin和end俩变量记录出栈的left,right
逻辑图
// 快速排序 非递归实现
void QuickSortNonR(int* a, int left, int right)
{
Stack st;
StackInit(&st);
StackPush(&st, right);
StackPush(&st, left);
while (!StackEmpty(&st))
{
int begin = StackTop(&st);
StackPop(&st);
int end = StackTop(&st);
StackPop(&st);
//单趟排序
int key = PartSort1(a, begin, end);
if (begin < key - 1)
{
//入栈先右后左
StackPush(&st, key - 1);
StackPush(&st, begin);
}
if (key + 1 < end)
{
//入栈先右后左
StackPush(&st, end);
StackPush(&st, key+1);
}
}
//销毁栈
StackDestroy(&st);
}
关于栈的功能实现代码就不放了
3.快排的时间复杂度分析
时间复杂度: O(n log n)
为什么为nlog n的原因分为俩个部分
- 在快排的单趟排序中,它的实践复杂度为N
而后面的log N是因为递归所产生的
而这部分的时间复杂度,也就是一棵树递归的深度 :也就是lon N
总结
尽管快速排序是一种高效的排序算法，但它也有一些缺点。以下是一些常见的快速排序缺点：
不稳定性： 快速排序是一种不稳定的排序算法。如果原始数据中存在相等元素，它们在排序后的相对顺序可能被改变，这与稳定性排序算法的特性相违背。
对重复元素的敏感性： 当待排序的数据中存在大量重复元素时，快速排序的性能可能下降。这是因为在分区过程中，相同的元素可能被分到不同的子数组中，导致递归深度增加，性能减弱。
对已经有序的数据表现差： 如果输入数据已经近乎有序，快速排序的性能会明显减弱。这是因为在每一轮的分区过程中，都会选择一个基准元素，如果数组已经有序，基准元素的选择可能导致不平衡的分区，使得算法失去了分治的优势。
空间复杂度高： 快速排序通常需要辅助空间来存储递归调用的栈，尤其是在递归调用层次较深时。在最坏情况下，递归调用的栈空间可能达到 O(n)，这可能导致栈溢出，尤其是对于大规模数据集。
不适合链表： 快速排序的实现通常依赖于数组的随机访问特性，而在链表中的随机访问效率较低。因此，对链表进行快速排序可能需要更复杂的实现，并且性能可能不如对数组进行快速排序。
尽管有这些缺点，快速排序在大多数情况下仍然是一种高效的排序算法，特别是对于大规模数据集。在实际应用中，可以根据具体情况选择合适的排序算法，以满足性能和稳定性的要求。