08 圆【小学】

最近做了圆的单元卷，满分110分的卷子只考了96分，算是一个很惨的分数了，换算成满分100分，我只考了87.2分。

圆的历史

古代人最早是从太阳，从阴历十五的月亮得到圆的概念的，那么是什么人作出第一个圆的呢?
18000年前的山顶洞人用一种尖状的石器来钻孔，一面钻不透，再从另一面钻。石器的尖是圆心，它的宽度的一半就是半径，这样以同一个半径和圆心一圈圈地转就可以钻出一个圆的孔。
到了陶器时代，许多陶器都是圆的。圆的陶器是将泥土放在一个转盘上制成的。
6000年前，半坡人就已经会造圆形的房顶了。
古代人还发现圆的木头滚着走比较省劲。后来他们在搬运重物时，就把几段圆木垫在重物的下面滚着走，这样就比扛着走省劲得多。
大约在6000多年前，美索不达米亚人，做出了世界上第一个轮子–圆的木轮。约在4000年前，人们将圆的木轮固定在木架上，这就成了最初的车子。
会作圆并且真正了解圆的性质，却是在2000多年前，是由我国的墨子给出圆的概念的:“一中同长也。”意思是说，圆有一个圆心，圆心到圆周的长都相等。这个定义比希腊数学家欧几里得给圆下定义要早100年。
圆，是数学中最基本的一个概念，其中却潜在地蕴涵了极其丰富的内涵。
岸边的海浪，雨后的彩虹，辽远星河中群星的轨迹，蘑菇的外形，机体内原子的结构，所有这些都与圆有着无法分割的联系。风滚草以翻转的方式在草原上移动;风叶籽以旋转的方式在地面上传播;激流以漩涡的方式汹涌向前;非洲的蚂蚁在遇到洪水威胁时，聚成一个小球，以滚动的方式逃生;一只苍蝇停在平静的湖面上，一条鱼冲上来把苍蝇吞下，湖面上荡起环形的波纹;溪流中的鹅卵石被水流磨成光滑的形状，在地面上可以像陀螺一样旋转……
从遥远的古代开始，自然界就以各种形式，存在者各种各样的圆。然而，这些圆也只能说是近似的圆，并不能等于真正意义上的圆。
但无论大自然如何精妙神奇，人类怎样聪明勤奋，在现实的几何世界中，终究不易找到那种神秘、玄妙的圆。
然而，这并不影响我们对圆的向往、崇拜和追求。千百年来，人们一直在了解圆、制造圆、应用圆。古埃及战车的轮子，建造金字塔的滚筒，物体落进水里泛起的水波纹，甚至你随手就能拿起一个圆……天上地下，处处都有圆。
圆，是数学中最基本的一个概念，其中却潜在地蕴涵了极其丰富的内涵。

圆的基础概念

圆不同于椭圆，我们的生活中其实更多出现的是椭圆。椭圆和圆的区别有以下三点：
1.圆形的圆心到任意边缘之间的距离都一定相等，而椭圆的圆心到任意边缘之间的距离不一定相等。
2.椭圆是圆锥曲线的一种，即圆锥与平面的截线的周长等于特定的正弦曲线在一个周期内的长度。用平面去截圆锥可能会出现椭圆。
3.在一平面内，一动点以一静点为中心，以一定长度旋转一周所形成的封闭曲线叫做圆。

我利用电脑画图，画出了一个圆。
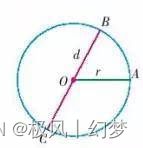
在使用圆规画图时，针尖的地方就是圆的圆心，针尖与笔尖的距离就是圆的半径长度，圆任意过圆心一条线且两段都在圆的边缘线上为直径，所有的直径都相等。直径的长度是半径的两倍。
圆心通常用字母O表示，半径通常用字母r表示，直径通常用字母d表示。

圆的周长

大家都知道圆的周长公式

C=2πr 或 C=πd

这个公式在小学与初中的教材中都是以实践法来推公式的。
一般情况下，会用线穿一个圆，就是要测量周长的圆。
将穿圆的线剪开，得到了圆的周长的测量品。
用尺子量一量，就可以知道长度。
经过多次测量，会发现圆的周长大约是直径的3.14倍。
因此，发明了圆周率π。
π表示的就是圆的周长与直径的比值。这个比值永远不变。

如果实在想知道圆的周长公式推导，也不是不可以。以下是我从某某网站搬运的回答：

对于半径为R的扇形，其圆心角为a，所对的弦长，由三角函数可得，2Rsin(a/2)，内接多边形周长为2π/aX2Rsin(a/2)，圆一周所对圆心角是2π，当然可以换个符号表示，不另讨论
相应的，外切多边形的算法类似，周长为2π/aX2Rtan(a/2)
当a接近于无穷小时，内接多边形周长为lim(a→0+)(2π/aX2Rsin(a/2))，外切多边形周长为
lim(a→0+)(2π/aX2Rtan(a/2))，对于极限lim(a→0+)(sina/a)，lim(a→0+)(tana/a)，a必须用弧度计算，如果a是角度，需要转化为弧度，这两个极限都是1
圆周长在这两个极限之间，大于内接圆周长，小于外切圆周长，而极限相等，由夹逼定理 2πRXlim(a→0+)(sin(a/2)/(a/2))=2πRXlim(a→0+)(tan(a/2)/(a/2))=2πR
所以圆周长等于2πR

圆的面积

圆的面积公式在教科书上也有明确记载

S=πr² 或 S=πd²÷4

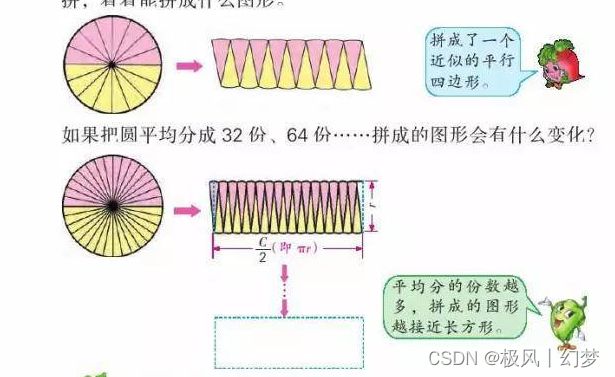
至于这个公式，是利用切割法推导的。
将圆沿直线切割得出的2n个扇形拼接，随着沿直径切割的刀数越来越多，扇形拼接而成的图形也会无限趋近长方形。由于长方形的宽就是半径r，长是周长的一半也就是πr，乘起来就可以得到πr²。

至于第二个公式，是利用乘方分配律得到的。

π(d÷2)²
=πd²÷2²
=πd²÷4

圆的主要考点

首先，考点肯定是包括圆的周长与面积的。但是想要考高分，还要记住以下几个定理：

S=π×C²÷16
在小学阶段，将π约等于3.14来计算结果。但到了中学阶段，可以在结果中直接写π。

1．圆是以圆心为对称中心的中心对称图形；围绕圆心旋转任意一个角度α,都能够与原来的重合．
2.顶点在圆心的角叫做圆心角．圆心到弦的距离叫做弦心距．
3．在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦的弦心距相等．
4．在同圆或等圆中,如果两个圆心角、两条弧、两条弦或两条弦的弦心距中有一组量相等,那么它们所对应的其余各组量都分别相等．
5．把整个圆周等分成360份,每一份弧是1°的弧．圆心角的度数和它所对的弧的度数相等．
6.圆是中心对称图形,即圆绕其对称中心(圆心)旋转180°后能够与原来图形重合,这一性质不难理解．圆和其他中心对称图形不同,它还具有旋转不变性,即围绕圆心旋转任意一个角度,都能够与原来的图形重合．
7.垂径定理 垂直于弦的直径平分这条弦,并且平分弦所对的两条弧
8.（1）平分弦（不是直径）的直径垂直于弦,并且平分弦所对的两条弧
（2）弦的垂直平分线经过圆心,并且平分弦所对的两条弧
（3）平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧
9.圆的两条平行弦所夹的弧相等
10.(1)一条弧所对的圆周角等于它所对的圆心角的一半.
(2)同弧或等弧所对的圆周角相等；同圆或等圆中,相等的圆周角所对的弧也相等.
(3)半圆(或直径)所对的圆周角是直角；90°的圆周角所对的弦是直径.
(4)如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形.
11.(1)圆是轴对称图形,经过圆心的每一条直线都是它的对称轴.
(2)垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.
(3)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
(4)弦的垂直平分线经过圆心,并且平分弦所对的两条弦.
(5)平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧.
(6)圆的两条平行弦所夹的弧度数相等.
12.圆是轴对称图形,经过圆心的每一条直线都是它的对称轴．
垂直于弦的直径平分这条弦,并且平分弦所对的两条弧．
13.平分弦(不是直径)的直径垂直与弦,并且平分弦所对的两条弧.
14.在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等,所对的弦的弦心距也相等.
15.在同圆或等圆中,相等的弦所对的弧相等,所对的圆心角相等,所对的弦的弦心距也相等.
16.同一个弧有无数个相对的圆周角.
17.弧的比等于弧所对的圆心角的比.
18.圆的内接四边形的对角互补或相等.
19.不在同一条直线上的三个点能确定一个圆.
20.直径是圆中最长的弦.
21.一条弦把一个圆分成一个优弧和一个劣弧.
22、圆的半径扩大到原来的n倍，面积就会扩大到原来的n²倍。
23、圆的面积扩大到原来的n倍，周长就会扩大到原来的✓n倍。
24、圆的半径扩大到原来的n倍，周长就会扩大到原来的n倍。

圆幂定理（相交弦定理、切割线定理及其推论(割线定理)统称为圆幂定理）
切线长定理（从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线,平分两条切线的夹角）
垂径定理（垂直于弦的直径平分这条弦,并且平分这条弦所对的两条弧）
弦切角定理（定义弦切角定理：弦切角的度数等于它所夹的弧的圆心角的度数的一半. (弦切角就是切线与弦所夹的角））