【Py/Java/C++三种语言OD2023C卷真题】20天拿下华为OD笔试之【贪心】2023C-变换最小字符串【欧弟算法】全网注释最详细分类最全的华为OD真题题解

题目描述与示例

题目描述

给定一个字符串s，最多只能进行一次变换，返回变换后能得到的最小字符串（按照字典序进行比较）

变换规则： 交换字符串中任意两个不同位置的字符。

输入描述

一串小写字母组成的字符串s

输出描述

按照要求进行变换得到的最小字符串

补充说明

s是都是小写字符组成

1 <= s.length <= 1000

示例一

输入

edcba

输出

adcbe

说明

选择索引0的e和索引4的a进行交换，得到字典序最小的字符串adcbe

示例二

输入

abcdef

输出

abcdef

说明

原字符串已经是最小字典序的字符了，无需进行交换。

解题思路

注意，本题和LeetCode670、最大交换几乎完全一致。

暴力法

数据范围最大为1000，时间复杂度为O(N^3)的暴力法可以通过绝大部分用例

所谓暴力法，就是枚举出所有不同的下标对(i, j)，交换s[i]和s[j]，找到交换完之后字典序最小的那一组。思路较为简单，故在此略去不表。一下讨论贪心的做法。

为什么是贪心

由于最多只能交换一次，贪心地思考一下这个问题：我们什么希望进行一个怎么样的交换？

换言之，怎么交换才能使得字典序尽可能地小？

考虑例子

aeadabc

原字符串中的第三个"a"是字典序最小且位置尽可能靠后的字符，这个字符应该优先地被交换到尽可能前的位置。由于索引0的字符是"a"，所以考虑索引1的字符"e"和第二个"a"交换。得到答案

aaadecb

从这个例子可以看出贪心的策略是：

1. 首选一个字典序尽可能小的字符（比如示例中选择字符"a"）
2. 如果有多个字典序最小的字符，则优先选择位置尽可能靠后的那个（比如示例中选择第三个字符"a"）
3. 将该字符交换到尽可能前的位置，即交换到第一个字典序大于该字符的位置（比如示例中索引1的位置）。

所以考虑逆序遍历原字符串，并且使用一个栈（类似一个单调栈），储存原字符串从右往左看遇到的字典序更小的字符的下标。

stack = list()
for i in range(n-1, -1, -1):
    if not stack or lst[i] < lst[stack[-1]]:
        stack.append(i)

最终这个栈一定会满足以下条件：

• 栈中储存的是原字符串的字符的下标i，
• i的取值自栈底向栈顶递减，即栈顶元素stack[-1]是在字符串s中位置最靠前的下标（满足了上述贪心策略2）
• lst[i]的取值自栈底向栈顶递减，即栈顶元素对应的下标在字符串中的取值s[i]是字典序最小的字符（满足了上述贪心策略1）

以例子s = aeadabc为例，栈中的结果是储存了最后三个字符"abc"的下标，即stack = [6, 5, 4]

接下来要考虑如何实现上述贪心策略的第三点。

我们可以从头到尾遍历原字符串lst，将下标i和栈顶元素stack[-1]、以及下标i对应的字符lst[i]和栈顶元素对应的字符lst[stack[-1]]进行比较。若

• i < stack[-1]，说明此时下标i的位置位于stack[-1]的左边，可以继续进行后续判断。若
  • lst[i] > lst[stack[-1]]，说明此时可以交换位置i和stack[-1]的两个字符，交换之且退出循环
  • lst[i] <= lst[stack[-1]]，说明此时不能进行交换，i需要继续增大
• i >= stack[-1]，说明此时下标i的位置已经不再位于stack[-1]的左边，此时不能再考虑栈顶元素，应该将其弹出

另外，由于涉及弹出操作，如果出现空栈情况，但尚未进行交换，则说明原字符串本身就是一个非递增序列，需要退出循环。综上，上述贪心操作的代码为

for i in range(n):
    if not stack:
        break
    if i > stack[-1]:
        if lst[i] > lst[stack[-1]]:
            lst[i], lst[stack[-1]] = lst[stack[-1]], lst[i]
            ans = "".join(lst)
            break
        else:
            continue
    else:
        stack.pop()

一个带图的例子

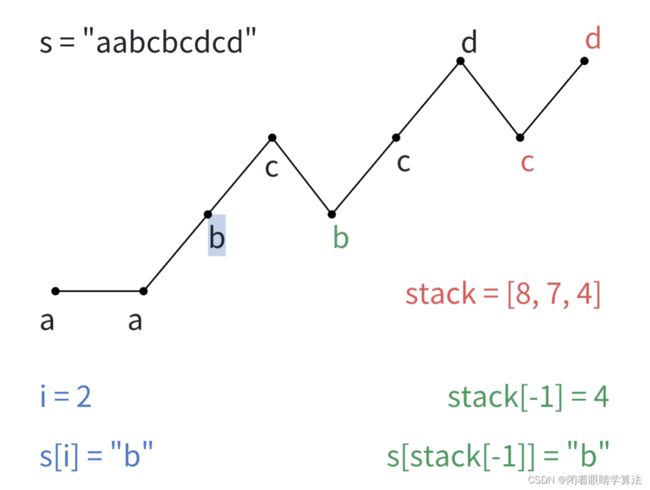
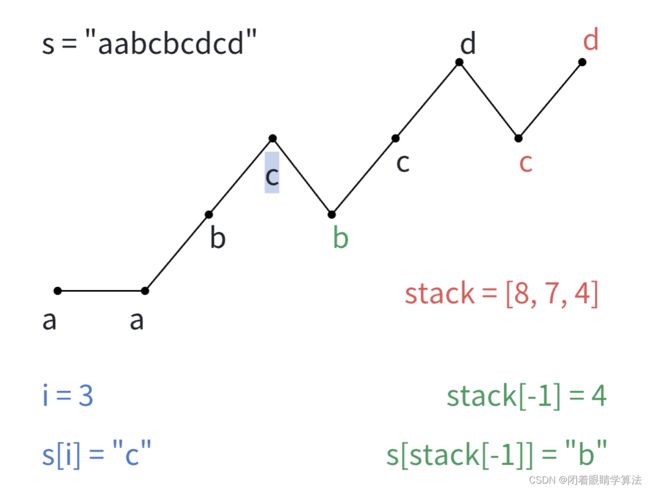
再举一个例子，s = "aabcbcdcd"，答案应该为ans = "aabbccdcd"，可以做出如下图

逆序遍历字符串s，构建栈stack = [8, 7, 4, 1]，为可能进行交换的那些对应字符字典序较小且靠后的位置。

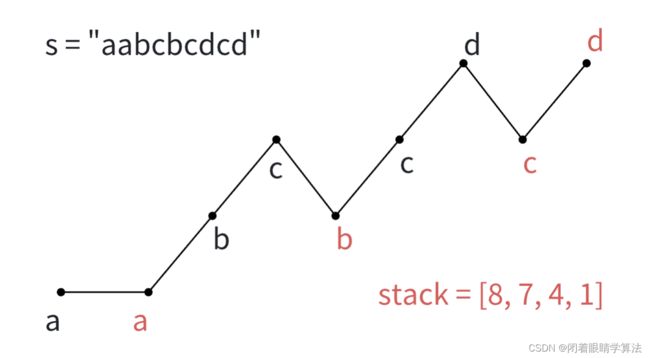
正序遍历i，反复拿出栈顶索引对应的元素s[stack[-1]]对应的字符和i对应的元素s[i]进行比较。会经历如下过程。

i < stack[-1]，但s[i] <= lst[stack[-1]]。不能做交换，i增加。

i >= stack[-1]，即i的位置不位于stack[-1]的左边，stack[-1]出栈，i增加。

i < stack[-1]，但s[i] <= lst[stack[-1]]。不能做交换，i增加。

i < stack[-1]，且s[i] > lst[stack[-1]]。进行交换，得到ans = "aabbccdcd"，是可以得到的字典序最小的结果。

代码

解法一：暴力法

python

# 题目：【贪心】2023C-变换最小字符串
# 分值：100
# 作者：闭着眼睛学数理化
# 算法：暴力
# 代码看不懂的地方，请直接在群上提问


# 输入原字符串
s = input()
# 初始化答案ans为s
ans = s
# 获得字符串s的长度n
n = len(s)
# 将s转化列表，方便交换操作
lst = list(s)

# 枚举下标i和下标j
for i in range(n-1):
    for j in range(i+1, n):
        # 令下标对(i, j)对应的两个字符进行交换
        lst[i], lst[j] = lst[j], lst[i]
        # 把交换后得到的字符串和ans进行比较，更新ans
        ans = min("".join(lst), ans)
        # 判断完毕后，下标对(i, j)对应的两个字符重新交换回去
        lst[i], lst[j] = lst[j], lst[i]

print(ans)

java

import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        String s = scanner.nextLine();
        char[] ans = s.toCharArray();
        int n = s.length();

        for (int i = 0; i < n - 1; i++) {
            for (int j = i + 1; j < n; j++) {
                // 令下标对(i, j)对应的两个字符进行交换
                char temp = ans[i];
                ans[i] = ans[j];
                ans[j] = temp;

                // 把交换后得到的字符串和ans进行比较，更新ans
                String current = new String(ans);
                if (current.compareTo(s) < 0) {
                    s = current;
                }

                // 判断完毕后，下标对(i, j)对应的两个字符重新交换回去
                temp = ans[i];
                ans[i] = ans[j];
                ans[j] = temp;
            }
        }

        System.out.println(s);
    }
}

cpp

#include 
#include 

int main() {
    std::string s;
    std::cin >> s;
    std::string ans = s;
    int n = s.length();

    for (int i = 0; i < n - 1; i++) {
        for (int j = i + 1; j < n; j++) {
            // 令下标对(i, j)对应的两个字符进行交换
            std::swap(s[i], s[j]);

            // 把交换后得到的字符串和ans进行比较，更新ans
            ans = std::min(s, ans);

            // 判断完毕后，下标对(i, j)对应的两个字符重新交换回去
            std::swap(s[i], s[j]);
        }
    }

    std::cout << ans << std::endl;

    return 0;
}

时空复杂度

时间复杂度：O(N^3)。双重循环需要O(N^2)的复杂度，每一次交换后，都需要进行合并字符串和比较的操作花费O(N)的时间复杂度，总的时间复杂度为O(N^3)

空间复杂度：O(1)。

解法二：贪心

python

# 题目：【贪心】2023C-变换最小字符串
# 分值：100
# 作者：闭着眼睛学数理化
# 算法：贪心，栈
# 代码看不懂的地方，请直接在群上提问


# 输入原字符串
s = input()
# 初始化答案ans为s
ans = s
# 获得字符串s的长度n
n = len(s)
# 将s转化列表，方便交换操作
lst = list(s)

# 构建一个栈，储存原字符串从右往左看遇到的字典序更小的字符的下标
stack = list()

# 逆序遍历字符串s
for i in range(n-1, -1, -1):
    # 如果栈是空栈，或者当前下标i对应的字符lst[i]小于栈顶下标对应的字符lst[stack[-1]]
    # 则将坐标i加入stack
    if not stack or lst[i] < lst[stack[-1]]:
        stack.append(i)

# 正序遍历字符串s
for i in range(n):
    # 若出现空栈情况，则退出循环
    if not stack:
        break
    # 如果当前下标i位于栈顶元素stack[-1]的左边
    # 则可以进行后续判断
    if i < stack[-1]:
        # 若当前字符大于栈顶元素对应的字符，则可以进行交换
        if lst[i] > lst[stack[-1]]:
            lst[i], lst[stack[-1]] = lst[stack[-1]], lst[i]
            ans = "".join(lst)
            break
        # 否则，考虑下一个i，这里的else也可以不写
        else:
            continue
    # 如果当前下标i不位于栈顶元素stack[-1]的左边
    # 则弹出栈顶元素，考虑下一个字典序较大但是位于较右位置的字符
    else:
        stack.pop()

print(ans)

java

import java.util.Scanner;
import java.util.Stack;

public class Main {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        String s = scanner.nextLine();
        char[] ans = s.toCharArray();
        int n = s.length();
        char[] lst = s.toCharArray();

        Stack<Integer> stack = new Stack<>();

        // 逆序遍历字符串s
        for (int i = n - 1; i >= 0; i--) {
            // 如果栈是空栈，或者当前下标i对应的字符lst[i]小于栈顶下标对应的字符lst[stack.peek()]
            // 则将坐标i加入stack
            if (stack.isEmpty() || lst[i] < lst[stack.peek()]) {
                stack.push(i);
            }
        }

        // 正序遍历字符串s
        for (int i = 0; i < n; i++) {
            // 若出现空栈情况，则退出循环
            if (stack.isEmpty()) {
                break;
            }
            // 如果当前下标i位于栈顶元素stack.peek()的左边
            // 则可以进行后续判断
            if (i < stack.peek()) {
                // 若当前字符大于栈顶元素对应的字符，则可以进行交换
                if (lst[i] > lst[stack.peek()]) {
                    char temp = lst[i];
                    lst[i] = lst[stack.peek()];
                    lst[stack.peek()] = temp;
                    ans = new String(lst).toCharArray();
                    break;
                }
                // 否则，考虑下一个i
            }
            // 如果当前下标i不位于栈顶元素stack.peek()的左边
            // 则弹出栈顶元素，考虑下一个字典序较大但是位于较右位置的字符
            else {
                stack.pop();
            }
        }

        System.out.println(new String(ans));
    }
}

C++

#include 
#include 
#include 

int main() {
    std::string s;
    std::cin >> s;
    std::vector<char> ans(s.begin(), s.end());
    int n = s.length();
    std::vector<char> lst(s.begin(), s.end());

    std::stack<int> stack;

    // 逆序遍历字符串s
    for (int i = n - 1; i >= 0; i--) {
        // 如果栈是空栈，或者当前下标i对应的字符lst[i]小于栈顶下标对应的字符lst[stack.top()]
        // 则将坐标i加入stack
        if (stack.empty() || lst[i] < lst[stack.top()]) {
            stack.push(i);
        }
    }

    // 正序遍历字符串s
    for (int i = 0; i < n; i++) {
        // 若出现空栈情况，则退出循环
        if (stack.empty()) {
            break;
        }
        // 如果当前下标i位于栈顶元素stack.top()的左边
        // 则可以进行后续判断
        if (i < stack.top()) {
            // 若当前字符大于栈顶元素对应的字符，则可以进行交换
            if (lst[i] > lst[stack.top()]) {
                std::swap(lst[i], lst[stack.top()]);
                ans = lst;
                break;
            }
            // 否则，考虑下一个i
        }
        // 如果当前下标i不位于栈顶元素stack.top()的左边
        // 则弹出栈顶元素，考虑下一个字典序较大但是位于较右位置的字符
        else {
            stack.pop();
        }
    }

    std::cout << std::string(ans.begin(), ans.end()) << std::endl;

    return 0;
}

时空复杂度

时间复杂度：O(N)。仅需一次遍历

空间复杂度：O(1)。栈的大小不会超过字符集大小26，可以视为常数级别时间复杂度。

---

华为OD算法/大厂面试高频题算法练习冲刺训练

• 华为OD算法/大厂面试高频题算法冲刺训练目前开始常态化报名！目前已服务100+同学成功上岸！

• 课程讲师为全网50w+粉丝编程博主@吴师兄学算法 以及小红书头部编程博主@闭着眼睛学数理化

• 每期人数维持在20人内，保证能够最大限度地满足到每一个同学的需求，达到和1v1同样的学习效果！

• 60+天陪伴式学习，40+直播课时，300+动画图解视频，300+LeetCode经典题，200+华为OD真题/大厂真题，还有简历修改、模拟面试、专属HR对接将为你解锁

• 可上全网独家的欧弟OJ系统练习华子OD、大厂真题

• 可查看链接 大厂真题汇总 & OD真题汇总(持续更新)

• 绿色聊天软件戳 od1336了解更多