深度学习图像分类相关概念简析+个人举例2（CNN相关原理概念与计算）

（2）卷积神经网络：英文全称Convolutional Neural Network,简称 CNN

  是一种常用于图像分类的深度学习模型，其主要特点是包含了卷积层和池化层，能够提取图像的局部特征。输入层、卷积层、池化层、全连接层和输出层都是卷积神经网络（CNN）中常见的层。这些层的组合和堆叠构成了卷积神经网络的基本架构。通过在不同层之间的连接和参数的学习，卷积神经网络能够高效地提取图像等复杂数据中的特征，并用于分类、检测和分割等任务。

 【1】卷积层：（Convolutional Layer）在CNN中，卷积层通过使用一系列的卷积核来提取图像的特征。每个卷积核都可以视为一种特征检测器，能够识别出图像中的某种特定特征。

  在卷积神经网络中，数乘和加和是卷积操作的基本计算步骤，也就是卷积操作。如果我们想解释数乘和加和，在此之前需要先引入卷积核和输入矩阵的概念。

  卷积核：卷积神经网络中的卷积核通常是一个小的矩阵。在图像识别任务中，一个常见的卷积核大小为3x3。卷积核的值是可学习的，它会根据网络的训练过程进行优化，对于图像识别任务，卷积核可以学习到检测边缘、纹理或物体的特定特征。

  就类似上面这玩意（3×3）~然后这玩意的每个格子里面都有数字的，这里面的数字就是它的值~这个数字，也就是初始值可以是随机的或者经过预训练的权重。

  假设这玩意3x3的卷积核，初始值为随机数，假设哦，我这里的例子假设不是都这数：

[[-0.167, 0.235, -0.563],

 [0.712, -0.321, 0.432],
 [-0.876, 0.102, -0.456]]
  这个卷积核可以应用于输入矩阵的每一个位置，进行卷积操作以提取特征。

  在实际应用中，卷积核的初始值通常会通过训练神经网络来学习，以使网络能够更好地适应特定的任务。

  输入矩阵：输入矩阵表示神经网络的输入数据，通常是一个多维的张量。在图像识别任务中，输入矩阵通常是一个三维张量，包含了图像的高度、宽度和通道数。例如，以RGB图像为例，输入矩阵可以表示为一个形状为[H, W, C]的张量，其中H为图像的高度，W为图像的宽度，C为图像的通道数。

  假设我们有一张RGB图像，它的尺寸为3x3像素。每个像素都由红、绿、蓝三个通道的强度值组成。输出矩阵的形状与输入矩阵的形状相同，都是3x3。

[[[255, 0, 0], [0, 255, 0], [0, 0, 255]],
 [[0, 0, 0], [255, 255, 255], [128, 128, 128]],
 [[0, 255, 0], [0, 0, 0], [255, 255, 0]]]

•   数乘操作是指将卷积核中的每个元素与输入数据对应位置的元素相乘。
•   加和操作是指将数乘结果进行累加求和。

 将每个数乘结果相加求和后得到一个值作为特征图中的一个像素值。

  怎么个算法呢？用上面的例子举例哈~

  在卷积中，我们将卷积核和输入矩阵的对应位置相乘，然后将所有乘积相加得到输出结果。数乘操作是将卷积核的每个元素与输入矩阵的对应元素相乘，加和操作是将所有乘积结果相加。

  首先，我们将输入矩阵和卷积核的对应位置相乘：

• 第一个元素相乘：(-0.167 * 255) + (0.235 * 0) + (-0.563 * 0) = -42.785
• 第二个元素相乘：(0.712 * 0) + (-0.321 * 255) + (0.432 * 0) = -82.155
• 第三个元素相乘：(-0.876 * 0) + (0.102 * 0) + (-0.456 * 255) = 116.28
• 第四个元素相乘：(-0.167 * 0) + (0.235 * 255) + (-0.563 * 0) = 59.925
• 第五个元素相乘：(0.712 * 255) + (-0.321 * 0) + (0.432 * 0) = 181.86
• 第六个元素相乘：(-0.876 * 0) + (0.102 * 255) + (-0.456 * 0) = 26.01
• 第七个元素相乘：(-0.167 * 0) + (0.235 * 0) + (-0.563 * 255) = 143.565
• 第八个元素相乘：(0.712 * 255) + (-0.321 * 0) + (0.432 * 0) = 181.86
• 第九个元素相乘：(-0.876 * 0) + (0.102 * 0) + (-0.456 * 255) = 116.28

  然后，我们将所有相乘结果相加得到输出结果： 输出结果 = -42.785 + (-82.155) + 116.28 + 59.925 + 181.86 + 26.01 + 143.565 + 181.86 + 116.28 = 721.625。

  因此，使用给定的卷积核和输入矩阵进行卷积操作后，得到的输出结果为721.625。这就是卷积操作中数乘和加和的具体应用示例。通过多次卷积操作，可以逐渐提取更高层次的特征。

【2】池化层（Pooling Layer）：在CNN中，池化层主要用于降低特征图的空间维度，减少参数数量和计算量，同时保持重要的特征。

  此处参考链接：卷积神经网络基础（卷积，池化，激活，全连接） - 知乎 (zhihu.com)

  上面链接中的博主提到了最小池化的概念，我这里只讲了最大和平均，最小和最大是同理的，感兴趣的兄弟看上面的链接一样一样的~跑题了！继续~

  在卷积神经网络（CNN）中，池化层是用来降低特征图的空间尺寸，减少参数数量，并且提取出图像的关键特征。池化操作在每个卷积层的特征图上进行，可以使用最大池化（Max Pooling）或平均池化（Average Pooling）。

  在最大池化中，池化层使用一个固定大小的滑动窗口，在每个窗口中选取最大特征值作为该窗口的输出值。这样可以保留最显著的特征，同时减少了特征图的尺寸。

  在平均池化中，池化层使用一个固定大小的滑动窗口，在每个窗口中计算特征值的平均值作为该窗口的输出值。这样可以减少特征图的尺寸，并且平滑特征值。

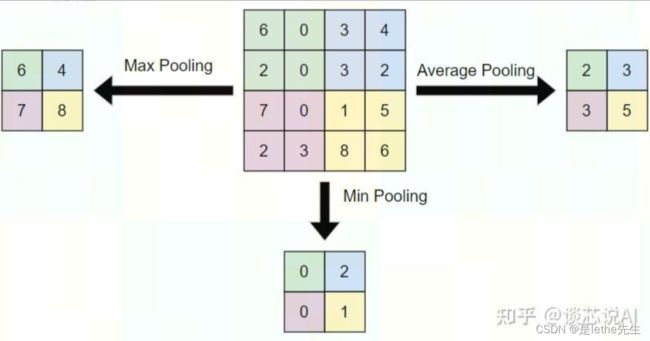
  借下上面链接中博主的图，我简单解释下，我个人理解的最大池化和平均池化~

  再说一遍，对于最大池化（Max Pooling），通常使用一个固定大小的滑动窗口，在每个窗口中选择窗口内的最大值作为池化后的输出值。

  这句话有点不讲人话，我们用上图中的例子解释就是：

已知池化层矩阵（4×4）：
6，0，3，4
2，0，3，2
7，0，1，5
2，3，8，6

  以输入矩阵为例，假设使用2x2的最大池化窗口，滑动步幅为2思密达~

那么计算过程如下：

• 最大池化窗口1：[6, 0; 2, 0]，最大值为6
• 最大池化窗口2：[3, 4; 3, 2]，最大值为4
• 最大池化窗口3：[7, 0; 2, 3]，最大值为7
• 最大池化窗口4：[1, 5; 8, 6]，最大值为8

  因此，最大池化的结果为：6, 4 7, 8

  同理，对于平均池化（Average Pooling），同样使用一个固定大小的滑动窗口，在每个窗口中计算特征值的平均值作为池化后的输出值。

  这种科技的东西的教程老是不讲人话，文绉绉的，同样以输入矩阵为例，假设使用2x2的平均池化窗口，滑动步幅为2！思密达~

  那么计算过程如下：

•   平均池化窗口1：[6, 0; 2, 0]，平均值为2
•   平均池化窗口2：[3, 4; 3, 2]，平均值为3
•   平均池化窗口3：[7, 0; 2, 3]，平均值为3
•   平均池化窗口4：[1, 5; 8, 6]，平均值为5

  平均，这里的平均就是平均数，窗口1直接6+0+2+0=8，8/4=2，平均数小学学的吧~这么一解释大家都懂了吧，然后就是按照上面的算下来平均池化的结果为：2, 3 ,3, 5~

  池化层具有以下几个相关概念：
1. 池化窗口大小：指定池化层使用的滑动窗口的大小。
2. 步幅（Stride）：指定滑动窗口在特征图上的移动步长。步幅较大会导致输出特征图的尺寸减小。
3. 填充（Padding）：在特征图的边缘填充0值，可以控制池化后特征图的尺寸。
4. 池化类型：最大池化和平均池化是两种常见的池化操作，根据任务需求选择使用哪种池化类型。

  池化层的运算和卷积层不同，不需要学习参数，主要通过固定的窗口大小、步幅和池化类型来进行。它的主要作用是减小特征图的尺寸，同时保留关键的特征信息，以便于后续的分类或其他任务。

  拿个代码来举例下吧~

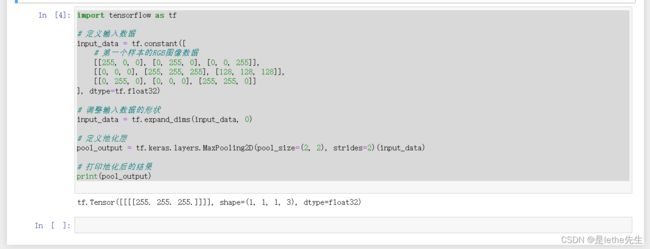
# 定义输入数据
input_data = tf.constant([
    # 第一个样本的RGB图像数据
    [[255, 0, 0], [0, 255, 0], [0, 0, 255]],
    [[0, 0, 0], [255, 255, 255], [128, 128, 128]],
    [[0, 255, 0], [0, 0, 0], [255, 255, 0]]
], dtype=tf.float32)

# 调整输入数据的形状
input_data = tf.expand_dims(input_data, 0)

# 定义池化层
pool_output = tf.keras.layers.MaxPooling2D(pool_size=(2, 2), strides=2)(input_data)

# 打印池化后的结果
print(pool_output)

• # 定义池化层
  pool_output = tf.keras.layers.MaxPooling2D(pool_size=(2, 2), strides=2)(input_data)
  

参数说明：

• inputs: 输入的特征图，通常是一个4维的张量，形状为[batch_size, height, width, channels]，其中batch_size表示批次大小，height和width表示特征图的高和宽，channels表示特征图的深度（通道数）。
• pool_size: 池化窗口的大小，通常为一个2维的整数列表或元组，如[2, 2]表示2x2的窗口大小。上面例子中的窗口大小~
• strides: 滑动步幅，通常为一个2维的整数列表或元组，如2表示步幅为2。
• 其他参数如padding（填充方式，默认为valid）、data_format（数据的格式，默认为channels_last）等可以根据需要进行设置。

 

  “max_pooling2d”，在上面的代码中，tf.layers.max_pooling2d函数实现了最大池化操作，它会对输入的特征图进行按窗口大小和步幅的设置进行采样，并返回每个窗口内元素的最大值作为输出。

  在这个特定的例子中，我们使用MaxPooling2D池化层，池化核大小为(2, 2)，步幅为2。由于输入数据形状是(3, 3, 3)（3行3列，深度为3），经过池化后得到的输出是(1, 1, 1, 3)。输出结果[[[[255. 255. 255.]]]]表示池化层对输入进行了池化操作，并选择了每个区域中最大值作为输出。这里的池化核大小为(2, 2)，所以对于输入数据的每个2x2的区域，选择最大值作为输出，因此输出为255.0。由于输入数据的深度为3，所以输出也是3个值，分别对应RGB通道的最大值。

【3】全连接层（Fully Connected Layer），也称为密集连接层或全连接层，是神经网络中的一种常见层类型。全连接层的计算过程是将输入的特征向量与权重矩阵相乘，并加上偏置项，然后经过激活函数的处理，得到最终的输出结果。

  全连接层是指神经网络中的每个神经元都与前一层的所有神经元相连接，每个连接都有一个权重。这种连接方式可以在一定程度上实现特征的组合与高阶抽象，但也导致参数数量庞大，容易出现过拟合的问题。

  详细计算和神经网络基础部分类似，举例见1，ANN的部分我觉得我写的很详细~下附链接：https://blog.csdn.net/weixin_55021541/article/details/136007157?spm=1001.2014.3001.5502

【4】在卷积神经网络（Convolutional Neural Network，CNN）中，输出层是网络的最后一层，用于生成最终的预测结果或特征表示。

  输出层的相关概念如下：

1. 神经元：输出层由若干个神经元组成，每个神经元对应一个类别或一个特定的特征。

2. 分类问题：对于分类问题，输出层通常使用全连接层来生成预测结果。每个神经元对应一个类别，通过激活函数（如Softmax）来将神经元的输出转化为概率分布，表示预测样本属于每个类别的概率。

3. 回归问题：对于回归问题，输出层通常只有一个神经元，并且不使用激活函数。输出层直接输出一个连续值，作为预测结果。

4. 特征表示：在一些任务中，输出层可以用于生成特征表示，而不是直接进行预测。在这种情况下，输出层的每个神经元对应的是网络中某个层的特征映射。这样可以利用网络学习到的特征表示来进行其他任务，如目标检测、图像生成等。

5. 损失函数：为了训练输出层，需要定义损失函数来度量预测结果与真实标签之间的差异。常见的损失函数包括交叉熵（Cross Entropy）用于分类问题，均方差（Mean Squared Error）用于回归问题。