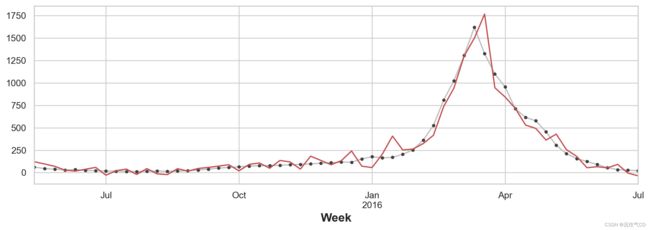
时间序列之周期性
什么是序列相关?
针对时间序列的趋势和季节性,我们可以很容易地利用“时间相关”的属性进行建模,即直接从时间索引中得出特征。但是有些情况下,一些时间序列只能利用“序列相关”属性,即使用序列的历史值作为特征。如下图所示,随着时间的推移,这些时间序列的结构可能并不明显,但如果与历史进行对比的话,结构就会很清晰。
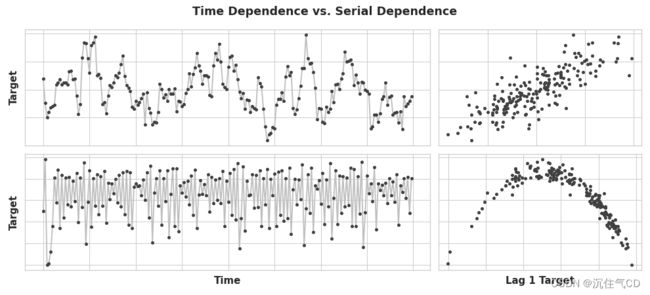
周期性
周期性是时间序列中序列相关最常见的一种表现方式,表示时间序列中增长和衰减的模式,某个时间序列中的取值依赖于之前的历史取值,但不一定依赖于时间步长。周期性是可以影响自身反应持续一段时间的系统特征,经济、流行病、火山爆发和类似的自然现象经常表现出周期性。
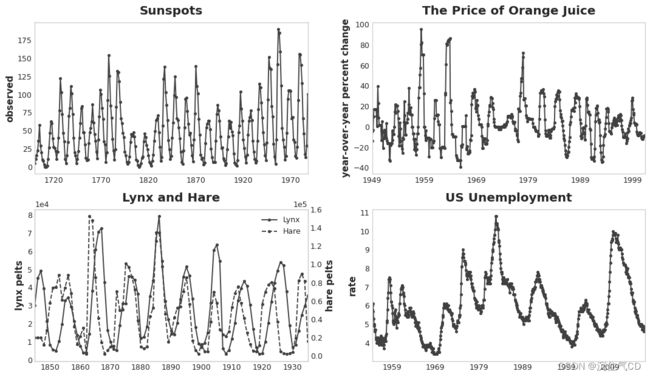
周期性与季节性的区别在于,周期性不一定像季节性那样依赖于时间,在一个周期中发生的事情与发生的特定日期关系不大,更多的是与最近发生的事情有关,这种相对于时间的独立性意味着周期性可能比季节性更不规律。
滞后序列和滞后图
为了研究时间序列中可能存在的序列相关,通常的做法是创建滞后的序列,滞后时间序列是指将序列取值向前移动一个或多个时间步,相当于将其索引中的时间向前移动一个或多个时间步。
这里给出一个示例:美国月度失业率(y)以及它的一阶和二阶滞后序列(y_lag_1、y_lag_2),我们可以使用滞后序列作为特征进行建模来预测美国失业率,即利用 y_lag_1 和 y_lag_2 来预测 y 。
import pandas as pd
reserve = pd.read_csv(
"data/ts-course-data/reserve.csv",
parse_dates={'Date':['Year', 'Month', 'Day']},
index_col='Date',
)
y = reserve.loc[:, 'Unemployment Rate'].dropna().to_period('M')
df = pd.DataFrame({
'y': y,
'y_lag_1': y.shift(1),
'y_lag_2': y.shift(2),
})
df.head()
| y | y_lag_1 | y_lag_2 | |
|---|---|---|---|
| Date | |||
| 1954-07 | 5.8 | NaN | NaN |
| 1954-08 | 6.0 | 5.8 | NaN |
| 1954-09 | 6.1 | 6.0 | 5.8 |
| 1954-10 | 5.7 | 6.1 | 6.0 |
| 1954-11 | 5.3 | 5.7 | 6.1 |
滞后图
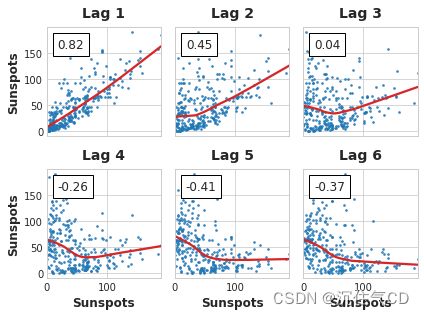
时间序列的滞后图显示了其取值与滞后取值的关系,通过观察滞后图,时间序列中的序列相关性通常会很明显,我们可以从美国失业率的滞后图中看到,当前失业率和历史失业率之间存在明显的线性关系。
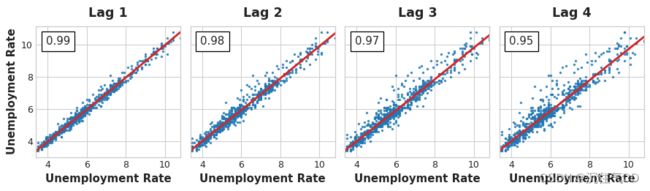
序列相关性最常用的度量方法是自相关,指一个时间点上时间序列的值与另一个时间点上时间序列的值之间的相关性,例如美国失业率与一阶滞后的相关性为 0.99,二阶为 0.98。
选择滞后阶数
当选择滞后阶数时,将全部强自相关的阶数纳入特征通常是无用的。例如,在美国失业率中,二阶滞后的自相关性很高,但很可能是来自于一阶滞后的衰减信息,如果二阶滞后不包含任何新的信息,在模型纳入一阶特征后,就没有理由再包含新的特征。
偏相关指一个滞后与之前所有滞后之间的相关性,即该滞后带来的新的信息,绘制相关图可以帮助我们选择要使用的滞后阶数。下图中 1 阶到 6 阶滞后超出了“不相关”的区域(蓝色),因此我们选择1 阶到 6 阶滞后特征进行建模(11 阶可能是误报)。
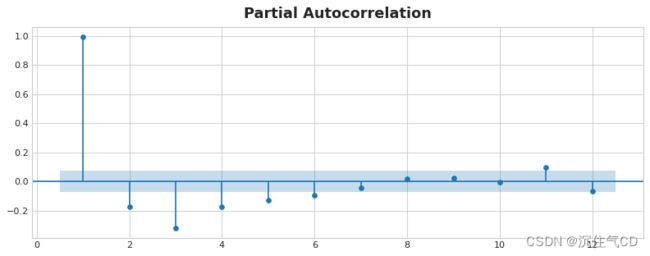
滞后特征的相关图本质上就像傅里叶特征的周期图一样。值得注意的是,自相关和偏相关的度量方式是线性依赖的,由于很多现实的时间序列存在非线性依赖关系,因此在选择滞后特征时,最好查看一下滞后图,例如太阳黑子序列是存在非线性依赖的,我们就可以通过自相关来忽略,像这样的非线性关系可以转换成线性关系,或者通过适当的算法学习。
示例——流感趋势
流感趋势数据集是 2009-2016 年的周统计流感就诊记录,我们的目标是预测未来几周的流感病例的数量。这里采用两种方法,一种是使用滞后特征来预测就诊情况;另一种是使用“另一组”时间序列的滞后特征来预测就诊情况:由谷歌捕获的与流感相关的搜索词。
from pathlib import Path
from warnings import simplefilter
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
from scipy.signal import periodogram
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from statsmodels.graphics.tsaplots import plot_pacf
# Configuration
simplefilter('ignore')
sns.set(style='whitegrid')
plt.rc('figure', autolayout=True, figsize=(11, 4))
plt.rc(
'axes',
labelweight='bold',
labelsize='large',
titleweight='bold',
titlesize=16,
titlepad=10,
)
plot_params = dict(
color='0.75',
style='.-',
markeredgecolor='0.25',
markerfacecolor='0.25',
)
%config InlineBackend.figure_format = 'retina'
def lagplot(x, y=None, lag=1, standardize=False, ax=None, **kwargs):
from matplotlib.offsetbox import AnchoredText
x_ = x.shift(lag)
if standardize:
x_ = (x_ - x_.mean()) / x_.std()
if y is not None:
y_ = (y - y.mean()) / y.std() if standardize else y
else:
y_ = x
corr = y_.corr(x_)
if ax is None:
fig, ax = plt.subplots()
scatter_kws = dict(
alpha=0.75,
s=3,
)
line_kws = dict(color='C3', )
ax = sns.regplot(x=x_,
y=y_,
scatter_kws=scatter_kws,
line_kws=line_kws,
lowess=True,
ax=ax,
**kwargs)
at = AnchoredText(
f'{corr:.2f}',
prop=dict(size='large'),
frameon=True,
loc='upper left',
)
at.patch.set_boxstyle('square, pad=0.0')
ax.add_artist(at)
ax.set(title=f'Lag {lag}', xlabel=x_.name, ylabel=y_.name)
return ax
def plot_lags(x, y=None, lags=6, nrows=1, lagplot_kwargs={}, **kwargs):
import math
kwargs.setdefault('nrows', nrows)
kwargs.setdefault('ncols', math.ceil(lags / nrows))
kwargs.setdefault('figsize', (kwargs['ncols'] * 2, nrows * 2 + 0.5))
fig, axs = plt.subplots(sharex=True, sharey=True, squeeze=False, **kwargs)
for ax, k in zip(fig.get_axes(), range(kwargs['nrows'] * kwargs['ncols'])):
if k + 1 <= lags:
ax = lagplot(x, y, lag=k + 1, ax=ax, **lagplot_kwargs)
ax.set_title(f'Lag {k + 1}', fontdict=dict(fontsize=14))
ax.set(xlabel='', ylabel='')
else:
ax.axis('off')
# plt.step(axs[-1, :], xlabel=x.name)
# plt.step(axs[:, 0], ylabel=y.name if y is not None else X.name)
fig.tight_layout(w_pad=0.1, h_pad=0.1)
return fig
data_dir = Path('data/ts-course-data')
flu_trends = pd.read_csv(data_dir / 'flu-trends.csv')
flu_trends.set_index(
pd.PeriodIndex(flu_trends.Week, freq='W'),
inplace=True
)
flu_trends.drop('Week', axis=1, inplace=True)
flu_trends.head()
| AInfluenza | AcuteBronchitis | BodyTemperature | BraunThermoscan | BreakAFever | Bronchitis | ChestCold | ColdAndFlu | ColdOrFlu | ColdVersusFlu | ColdVsFlu | ContagiousFlu | CoughFever | CureFlu | CureTheFlu | DangerousFever | DoIHaveTheFlu | EarThermometer | EarlyFluSymptoms | Expectorant | ExposedToFlu | FeverCough | FeverFlu | FeverReducer | FightTheFlu | FluAndCold | FluAndFever | FluCare | FluChildren | FluComplications | FluContagiousPeriod | FluContagious | FluCough | FluDuration | FluFever | FluGerms | FluHeadache | FluHowLong | FluInChildren | FluIncubationPeriod | ... | OverTheCounterFluMedicine | OverTheCounterFlu | PainfulCough | Pneumonia | RapidFlu | ReduceAFever | ReduceFever | RemediesForFlu | RemediesForTheFlu | RespiratoryFlu | Robitussin | SignsOfFlu | SignsOfTheFlu | SinusInfections | Sinus | StrepThroat | Strep | SymptomsOfBronchitis | SymptomsOfFlu | SymptomsOfInfluenza | SymptomsOfPneumonia | SymptomsOfTheFlu | TakingTemperature | Tessalon | TheFluVirus | TheFlu | Thermoscan | TreatFlu | TreatTheFlu | TreatingFlu | TreatingTheFlu | TreatmentForFlu | TreatmentForTheFlu | Tussin | Tussionex | TypeAInfluenza | UpperRespiratory | WalkingPneumonia | WhatToDoIfYouHaveTheFlu | FluVisits | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Week | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2009-06-29/2009-07-05 | 36 | 20 | 43 | 27 | 11 | 22 | 16 | 7 | 3 | 8 | 4 | 5 | 15 | 3 | 5 | 18 | 2 | 29 | 7 | 36 | 21 | 15 | 15 | 19 | 13 | 7 | 22 | 9 | 5 | 3 | 8 | 5 | 16 | 12 | 15 | 10 | 15 | 6 | 4 | 7 | ... | 14 | 11 | 10 | 33 | 8 | 27 | 19 | 6 | 6 | 9 | 22 | 6 | 4 | 27 | 44 | 36 | 43 | 15 | 6 | 8 | 19 | 4 | 26 | 23 | 3 | 3 | 34 | 6 | 5 | 4 | 16 | 6 | 13 | 25 | 34 | 30 | 25 | 24 | 15 | 180 |
| 2009-07-06/2009-07-12 | 25 | 19 | 40 | 31 | 10 | 21 | 11 | 6 | 8 | 8 | 7 | 6 | 13 | 3 | 1 | 19 | 5 | 35 | 12 | 21 | 16 | 13 | 15 | 18 | 7 | 6 | 20 | 7 | 4 | 4 | 7 | 6 | 14 | 17 | 15 | 13 | 16 | 7 | 4 | 8 | ... | 6 | 7 | 19 | 33 | 5 | 23 | 14 | 3 | 6 | 6 | 21 | 6 | 6 | 26 | 42 | 34 | 40 | 12 | 5 | 7 | 18 | 4 | 23 | 23 | 4 | 3 | 25 | 12 | 9 | 13 | 16 | 7 | 8 | 27 | 32 | 27 | 28 | 29 | 9 | 115 |
| 2009-07-13/2009-07-19 | 24 | 30 | 45 | 20 | 12 | 20 | 20 | 6 | 6 | 8 | 4 | 6 | 11 | 3 | 2 | 17 | 8 | 29 | 9 | 24 | 7 | 11 | 13 | 13 | 7 | 6 | 20 | 9 | 5 | 7 | 9 | 6 | 13 | 16 | 13 | 5 | 14 | 7 | 5 | 6 | ... | 6 | 7 | 19 | 32 | 11 | 15 | 17 | 7 | 6 | 13 | 19 | 5 | 7 | 28 | 43 | 32 | 39 | 15 | 6 | 6 | 14 | 4 | 30 | 18 | 4 | 3 | 23 | 8 | 11 | 12 | 16 | 6 | 9 | 24 | 28 | 25 | 25 | 25 | 9 | 132 |
| 2009-07-20/2009-07-26 | 23 | 19 | 40 | 15 | 10 | 19 | 12 | 7 | 10 | 15 | 3 | 5 | 14 | 3 | 2 | 14 | 2 | 18 | 9 | 18 | 17 | 14 | 12 | 18 | 4 | 7 | 14 | 8 | 5 | 5 | 8 | 5 | 13 | 7 | 12 | 14 | 16 | 6 | 3 | 8 | ... | 8 | 6 | 12 | 32 | 20 | 23 | 12 | 7 | 11 | 6 | 18 | 6 | 4 | 27 | 44 | 30 | 35 | 15 | 5 | 6 | 16 | 4 | 22 | 18 | 4 | 3 | 13 | 5 | 6 | 7 | 8 | 5 | 12 | 21 | 26 | 26 | 29 | 24 | 13 | 109 |
| 2009-07-27/2009-08-02 | 27 | 21 | 44 | 20 | 11 | 19 | 17 | 8 | 10 | 15 | 6 | 5 | 11 | 3 | 5 | 17 | 5 | 28 | 12 | 30 | 13 | 11 | 15 | 14 | 6 | 8 | 23 | 11 | 7 | 7 | 9 | 5 | 14 | 15 | 15 | 16 | 23 | 7 | 6 | 7 | ... | 9 | 8 | 9 | 34 | 17 | 19 | 14 | 8 | 7 | 10 | 20 | 7 | 6 | 28 | 43 | 30 | 36 | 12 | 6 | 6 | 14 | 5 | 33 | 17 | 6 | 4 | 23 | 8 | 10 | 6 | 8 | 8 | 12 | 33 | 29 | 21 | 27 | 30 | 9 | 120 |
5 rows × 130 columns
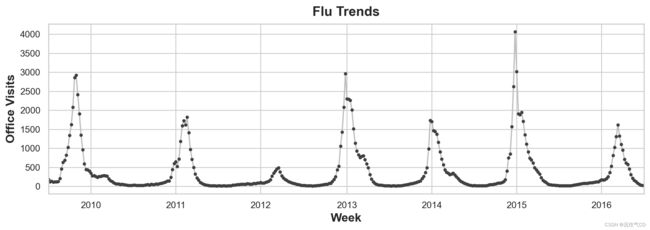
ax = flu_trends.FluVisits.plot(title='Flu Trends', **plot_params)
_ = ax.set(ylabel='Office Visits')
流感趋势数据表现出了不规则的周期性,而不是规则的季节性:高峰期往往出现在新年前后,但或早或晚、时大时小。用滞后特征对周期性进行建模,可以让我们对不断变化的情形做出动态反应,而不是像季节性特征那样收到精确日期和时间的限制。
_ = plot_lags(flu_trends.FluVisits, lags=12, nrows=2)
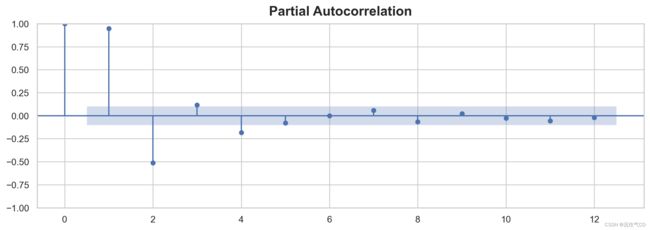
_ = plot_pacf(flu_trends.FluVisits, lags=12)
滞后图表明,FluVisits 与其滞后特征主要是线性关系,根据相关图,这种关系可以使用一阶、二阶、三阶和四阶滞后特征来捕获,这里使用 0 填充滞后创建后的缺失值。
def make_lags(ts, lags):
return pd.concat(
{
f'y_lag_{i}': ts.shift(i)
for i in range(1, lags + 1)
},
axis=1
)
X = make_lags(flu_trends.FluVisits, lags=4)
X = X.fillna(0.0)
注意当使用滞后特征时,我们仅限于预测其滞后值可用的时间步长,例如使用在星期一的一阶滞后特征,是无法预测星期三情况的,因为如果要预测星期三的值我们就需要星期二的一阶滞后特征,而星期二还没有发生。
# Create target series and data splits
y = flu_trends.FluVisits.copy()
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=60, shuffle=False)
# Fit and predict
model = LinearRegression() # `fit_intercept=True` since we didn't use DeterministicProcess
model.fit(X_train, y_train)
y_pred = pd.Series(model.predict(X_train), index=y_train.index)
y_fore = pd.Series(model.predict(X_test), index=y_test.index)
ax = y_train.plot(**plot_params)
ax = y_test.plot(**plot_params)
ax = y_pred.plot(ax=ax)
_ = y_fore.plot(ax=ax, color='C3')
ax = y_test.plot(**plot_params)
_ = y_fore.plot(ax=ax, color='C3')
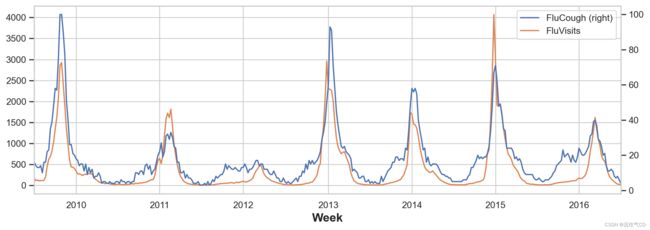
为了改善预测,我们尝试找到领先指标,这里我们采用的方法是在训练集中添加一些由谷歌趋势测量的流感相关搜索词的流行度。例如,将搜索词 FluCough 与目标搜索词 FluVisits 进行对比表明,这类搜索词可能是有用的先行指标:流感相关搜索往往在就诊前几周变得更受欢迎。
ax = flu_trends.plot(
y=['FluCough', 'FluVisits'],
secondary_y='FluCough',
)
search_terms = ["FluContagious", "FluCough", "FluFever", "InfluenzaA", "TreatFlu", "IHaveTheFlu", "OverTheCounterFlu",
"HowLongFlu"]
# Create three lags for each search term
X0 = make_lags(flu_trends[search_terms], lags=3)
X0.columns = [' '.join(col).strip() for col in X0.columns.values]
# Create four lags for the target, as before
X1 = make_lags(flu_trends['FluVisits'], lags=4)
# Combine to create the training data
X = pd.concat([X0, X1], axis=1).fillna(0.0)
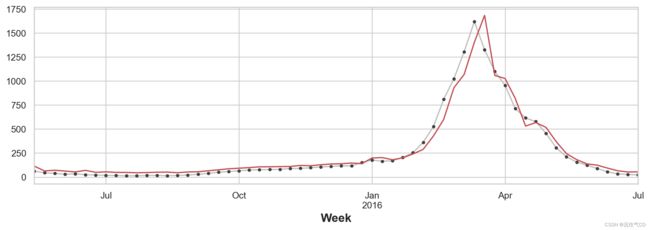
虽然这样进行预测比较粗糙,但模型能够更好地预测流感访问量的突然增加,这表明新添加的几个指标是有效的。
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=60, shuffle=False)
model = LinearRegression()
model.fit(X_train, y_train)
y_pred = pd.Series(model.predict(X_train), index=y_train.index)
y_fore = pd.Series(model.predict(X_test), index=y_test.index)
ax = y_test.plot(**plot_params)
_ = y_fore.plot(ax=ax, color='C3')
本示例所展示的时间序列是“纯周期性”的,没有明显的趋势或季节性,但在现实世界中同时拥有趋势、季节性和周期性的时间序列是很常见的,这时只需要为每个部分添加适当的特征来进行建模即可,也可以通过混合模型来学习单个部分。