动态规划-经典dp(打家劫舍,股票等)
1.常规dp
1.1 爬楼梯
1.1.1 爬楼梯
由于求的是组合数,我们将不同路径相加即可
dp定义:
dp[i]为爬到第i阶楼梯的方法数;
转移方程:
dp[i] = dp[i-2] +dp[i-1];初始化:
由于涉及到i-2和i-1,那么我们要从i=2开始遍历,因此要初始化dp[0] = 0,dp[1] = 1(根据定义)
遍历顺序:
从左往右
完整代码:
class Solution {
public:
int climbStairs(int n) {
vector dp(n+1,0);
dp[0] = 0;
dp[1] = 1;
if(n==1)return 1;
dp[2] = 2;
for(int i =3;i<=n;i++){
dp[i] = dp[i-2] +dp[i-1];
}
return dp[n];
}
}; 1.1.2 使用最小花费爬楼梯
此题和上一题非常类似,只要理解题意就不难
由于是求解最优路径,我们使用min而不是相加,同时我们要理解假如有n层台阶,那么顶层就是顶n+1层(由题意可知):
1)因此我们设置dp大小为n+1
2)同时初始化时,不要初始化错误,
如果我们认为dp[1]是跳过0 1 两级就错了,会初始化为:
dp[0] = 0;
dp[1] = min(cost[0],cost[1]);实际上dp[1]表示跳到第1级台阶上面的顶层,而dp[0]表示顶层就是地板的下一级
dp[0] = 0;
dp[1] = 0;其实不用专门初始化,dp[i]全为0即可
其他不多赘述,详细步骤参考下面代码和1.1.1:
class Solution {
public:
int minCostClimbingStairs(vector& cost) {
int n = cost.size();
vector dp(n+1,0);
dp[0] = 0;
dp[1] = min(cost[0],cost[1]);
for(int i =2;i <= n;i++){
dp[i] = min(dp[i- 1]+cost[i-1],dp[i-2]+cost[i-2]);
}
return dp[n];
}
}; 1.2 不同路径
1.2.1 不同路径
这样的题显然会第一时间想到dfs,但这里使用dfs会超时,使用备忘录优化的话时间复杂度和dp相同,因此我们直接使用dp来做
dp定义:
这类问题的dp定义很简单,要么就是表示组合数要么就是最优路径,且一般为二维dp
此题dp[i][j]表示走到(i,j)有多少路径
转移方程:
转移方程也比较固定,dp[i][j]由dp[i-1][j] 和dp[i][j1](上面和左边,因为机器人只能这样走)转移过来
此处为:
dp[i][j] = dp[i-1][j]+dp[i][j-1];初始化:
注意二维dp同时是从左上角往右下角更新,因此,我们要初始化第一行和第一列 ,具体怎么初始化,根据定义即可
此处为:
for(int i = 0;i < n;i++)dp[i][0] = 1;
for(int i = 0;i < m;i++)dp[0][i] = 1;遍历方向:
斜向下
完整代码:
class Solution {
public:
int uniquePaths(int m, int n) {
vector> dp(n,vector(m,0));
for(int i = 0;i < n;i++)dp[i][0] = 1;
for(int i = 0;i < m;i++)dp[0][i] = 1;
for(int i = 1; i < n;i++)
for(int j = 1;j 1.2.2 不同路径2
核心和上一题相同,注意的点:
1)只有当一个点没有障碍时我们才能更新这个点
2)我们可以从有障碍的点推到无障碍的点,因为有障碍的点路径为0,相当于没有使用,也即是之前的转移方程不用变,加一点限制条件即可:
if(obstacleGrid[i][j]!=1){
dp[i][j] = dp[i-1][j]+dp[i][j-1];
}3)初始化时,如果一行里有一个障碍,那么障碍之后都走不通了,也就是第一个障碍及其之后初值都为0
for(int i =0;i 其余没有什么注意点,完整代码如下:
class Solution {
public:
int uniquePathsWithObstacles(vector>& obstacleGrid) {
int m = obstacleGrid.size();
int n = obstacleGrid[0].size();
vector> dp(m,vector(n,0));
for(int i =0;i 1.2.3 最小路径和
核心与上面两题相同,注意以下点:
1)这里是求最优路径不是组合数,因此使用min
2)每次更新当前点,需要加上当前点的数字
dp[i][j] = min(dp[i-1][j]+grid[i][j],dp[i][j-1]+grid[i][j]);3)初始化也是根据定义来,第0行和第0列结果都是递增的
for(int i = 0;i < m;i++){
sum1+= grid[i][0];
dp[i][0] = sum1;
}
for(int i = 0;i < n;i++){
sum2+= grid[0][i];
dp[0][i] = sum2;
}完整代码如下:
class Solution {
public:
int minPathSum(vector>& grid) {
int m = grid.size(),n = grid[0].size();
vector> dp(m,vector(n,0));
int sum1= 0,sum2=0;
for(int i = 0;i < m;i++){
sum1+= grid[i][0];
dp[i][0] = sum1;
}
for(int i = 0;i < n;i++){
sum2+= grid[0][i];
dp[0][i] = sum2;
}
for(int i =1;i < m;i++)
for(int j = 1;j < n;j++){
dp[i][j] = min(dp[i-1][j]+grid[i][j],dp[i][j-1]+grid[i][j]);
}
return dp[m-1][n-1];
}
}; 1.3 整数拆分
dp定义:
dp[j]为j经过至少2次拆分得的最大乘积和
我们从后往前思考,要想得到dp[n],我们就把先拆为两份dp[i - j] 和 j, dp[i - j]中包含k-1中拆解,j表示一种拆解,这样往前递推
注意,这里容易误写为:
dp[i] = max(dp[i-j] * j ,dp[i]);相当于只把j拆为dp[i - j]和j这两部分,我们认为dp[i - j]就包含了i - j的所有拆分情况,但是我们没有考虑dp定义,dp[i - j]表示将i - j至少拆为了2份,那么上式就表示将dp[i]至少拆为三份(2+1)和dp定义不符
所以我们要知道,i - j为一个没拆分的整体这种情况并没有归类到dp[i - j]中,所以我们要单独将其列出来,如下:
dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));初始化:
这里我只初始化dp[2] = 1,从dp[i]的定义来说,拆分数字2,得到的最大乘积是1
dp[2] = 1;遍历顺序:
dp[i] 是依靠 dp[i - j]的状态,所以遍历i一定是从前向后遍历,先有dp[i - j]再有dp[i]。
for(int i = 3;i <= n;i++)
for(int j = 1;j < i;j++){
dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));//max(dp[i-j] * j ,dp[i]);
}//因为定义的问题,dp[i-j]至少包含两个数,不然不对注意 枚举j的时候,是从1开始的。从0开始的话,那么让拆分一个数拆个0,求最大乘积就没有意义了。
完整代码如下:
class Solution {
public:
int integerBreak(int n) {
vector dp(n+1,0);
// dp[0] = 0;
// dp[1] = 1;
dp[2] = 1;
for(int i = 3;i <= n;i++)
for(int j = 1;j < i;j++){
dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));//max(dp[i-j] * j ,dp[i]);
}//因为定义的问题,dp[i-j]至少包含两个数,不然不对
return dp[n];
}
}; 优化:
因为拆分一个数n 使之乘积最大,那么一定是拆分成m个近似相同的子数相乘才是最大的。
例如 6 拆成 3 * 3, 10 拆成 3 * 3 * 4。 100的话 也是拆成m个近似数组的子数 相乘才是最大的。
只不过我们不知道m究竟是多少而已,但可以明确的是m一定大于等于2,既然m大于等于2,也就是 最差也应该是拆成两个相同的 可能是最大值。
那么 j 遍历,只需要遍历到 n/2 就可以,后面就没有必要遍历了,一定不是最大值。
class Solution {
public:
int integerBreak(int n) {
vector dp(n+1,0);
// dp[0] = 0;
// dp[1] = 1;
dp[2] = 1;
for(int i = 3;i <= n;i++)
for(int j = 1;j <= i/2;j++){
dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));//max(dp[i-j] * j ,dp[i]);
}//因为定义的问题,dp[i-j]至少包含两个数,不然不对
return dp[n];
}
}; 2.打家劫舍
2.1 打家劫舍 1
这道题类似子序列问题的dp定义
首先要明确选择和状态是什么
1)选择:
是否抢nums[i]
2)状态:
当前金额
dp定义:
只有一个状态,所以使用一维dp,dp[i]为nums[0,i](不一定会包括i)抢劫到的最大金额
转移方程:
因为只有一个选择我们要做的就是分情况讨论,抢劫和不抢劫两种情况:
1)不抢劫:
继承dp[i-1]的结果
2)抢劫:
假如dp[i-1]中nums[i-1]被抢过,那么我们不能使用dp[i-1] + nums[i],只有使用dp[i-2] + nums[i]
假如dp[i-1】中nums[i-1]没被抢过,那么dp[i-1]就等于dp[i-2],那么结果也是dp[i-2] + nums[i]
因此转移方程如下:
dp[i] = max(dp[i-2]+nums[i],dp[i-1]);初始化:
由于我们使用i-2更新i,那么要从i=2开始遍历,那么就要根据定义初始化dp[0]和dp[1]:
dp[0] = nums[0];
dp[1] = max(nums[0],nums[1]); 遍历方向:
顺序遍历即可
完整代码如下:
class Solution {
public:
int rob(vector& nums) {
int n = nums.size();
if(n==1)return nums[0];
vector dp(n);
dp[0] = nums[0];
dp[1] = max(nums[0],nums[1]);
for(int i = 2; i < n; i++){
dp[i] = max(dp[i-2]+nums[i],dp[i-1]);
}
return dp[n-1];
}
}; 2.1.2 打家劫舍2
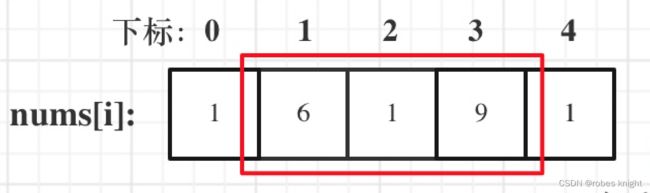
此题为环形数组打家劫舍,其实就是打家劫舍1的变种,我们分清各种情况即可
一开始的错误想法:
由于是环形,我们直接将nums[0]拼接到nums之后,在新的nums进行打家劫舍
1)如果开头的nums[0]被抢了,就用金额-nums[0]
2)如果开头的nums[0]没有被抢,就不用减
class Solution {
public:
int rob(vector& nums) {
int n = nums.size();
if(n==1)return nums[0];
nums.push_back(nums[0]);
vector dp(n+1,0);
dp[0] = nums[0];
dp[1] = max(nums[0],nums[1]);
for(int i = 2;i <= n;i++)
dp[i] = max(dp[i - 1],dp[i - 2]+nums[i]);
return dp[n] - nums[0];
}
}; 但问题在于,我们的策略都是动态自动执行的,并不能通过nums就知道nums[0]该不该抢,因此上述代码没法考虑到第一个nums[0]没被抢的那一部分情况
正确做法:错误做法里,主要是矛盾点在于我们将nums[0]包含进了打劫的范围,从而造成情况难以区分
现在,我们直接将不打算打劫的地方剔除,然后分情况讨论,并且不将nums[0]拼接到后面
我们只要让nums[0]和nums[n-1]分开即可 ,下面3种情况,纳入范围不一定取得到,但是不纳入一定取不到
1)考虑不包含首尾元素
2)考虑包含首元素,不包含尾元素
3) 考虑包含尾元素,不包含首元素
4)首尾都取
虽然首尾都取时,也会有部分情况满足题意,但是我们仔细分析,如果满足题意,那么一定是上面三种情况之一,所以4)中的有效部分已经被上面三种情况所包含,因此不做考虑了
而情况二 和 情况三 都包含了情况一了,所以只考虑情况二和情况三就可以了。
我们只要两种情况分别进行打家劫舍,然后结果取最大值即可
我们只需将打家劫舍的基础版增加一个区间限制,然后套用即可:
class Solution {
public:
int rob_tmp(vector& nums,int start,int end) {
int n = nums.size();
if(end == start)return nums[start];
vector dp(n,0);
dp[start] = nums[start];
dp[start+1] = max(nums[start],nums[start+1]);
for(int i = start+2;i < end;i++)
dp[i] = max(dp[i - 1],dp[i - 2]+nums[i]);
return dp[end-1];
}
int rob(vector& nums) {
int n = nums.size();
if(n==1)return nums[0];
if(n==2)return max(nums[0],nums[1]);
int res1 = rob_tmp(nums,1,n);
int res2 = rob_tmp(nums,0,n-1);
return max(res1,res2);
}
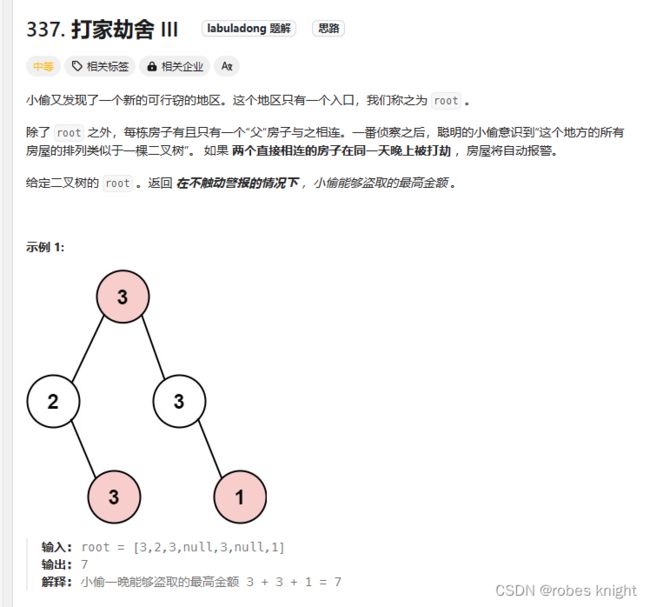
}; 2.1.3 打家劫舍3
涉及二叉树,复习之后再说
3.股票买卖的最佳时机
3.1 框架 -股票买卖的最佳时机4
我们以较难但是很全面的4为框架,对这一类题进行解答
首先我们要找到选择和状态:
1)选择:
每天都有三种「选择」:买入、卖出、无操作,我们用 buy, sell, rest 表示这三种选择。
但问题是,并不是每天都可以任意选择这三种选择的,因为 sell 必须在 buy 之后,buy 必须在 sell 之后。那么 rest 操作还应该分两种状态,一种是 buy 之后的 rest(持有了股票),一种是 sell 之后的 rest(没有持有股票)。而且别忘了,我们还有交易次数 k 的限制,就是说你 buy 还只能在 k > 0 的前提下操作。
2)状态:
这个问题的「状态」有三个,第一个是天数,第二个是允许交易的最大次数,第三个是当前的持有状态(我们不妨用 1 表示持有,0 表示没有持有)。
不要把当前持有状态和是否继续持有混为一谈,一个当前是否还持有股票,另一个是对当天股票的决策
(1)dp定义:
dp[i][j][0]第i天时,我们已经进行了最多j次交易,此时手上没有股票,此时我们利润(身上剩的钱)为dp[i][j][0]
dp[i][j][1]第i天时,我们已经进行了最多j次交易,此时手上有股票,此时我们利润(身上剩的钱)为dp[i][j][1]
(2)转移方程:
这里要理解转移方程,画出状态转移图时最直观的
画出状态转移图(以某一天为例):
完整的状态转移图:
我们发现图中没有对最大交易次数进行比较明显的解释,这部分是本问题的理解难点,写转移方程的时候会具体说明
我们分两部分定义dp数组,因此自然而然更新也要分两部分:
1)当天手上并没有股票:
max( 今天选择 rest, 今天选择 sell )
今天选择 rest = 保留昨天的无股票
今天选择 sell = 昨天有,今天卖了,由于卖了股票,利润增加
dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i])2)当天手上有股票:
max( 今天选择 rest, 今天选择 buy )
今天选择 rest = 保留昨天的有股票
今天选择 buy = 昨天没有股票今天买入
注意,我们最开始分析三种选择时发现,每一种选择都有限制
因为 sell 必须在 buy 之后;buy 必须在 sell 之后; 交易还只能在 k > 0 的前提下操作。
前两种通过当前手上是否持有股票实现了(因为不能同时进行多笔交易,所以我们0也可以表示卖了,1表示买了),那么k的限制如何实现呢?
我们可以在buy和sell的时候进行k的变更,但是如果在sell才进行变更,对于有些只买不卖的情况,k会错误,所以我们选择从buy开始就更改k
我们将k引入,如下:
dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i])解释:
k为当前允许的最大次数,由于今天要进行购买,那么也就是截至前一天为止k次交易次数不能全部使用,也就是最多交易了k-1次
其他情况,由于没有涉及到buy,交易次数不改变
完整转移方程如下:
dp[i][j][0] = max(dp[i-1][j][0],dp[i-1][j][1]+prices[i]);
dp[i][j][1] = max(dp[i-1][j][1],dp[i-1][j-1][0]-prices[i]);(3)初始化:
在本题我们只需要初始化i=0的二维数组即可,由于第0天肯定赚不了,所以利润全为0即可
(4)遍历方向 :
顺序遍历
完整代码如下:
class Solution {
public:
int maxProfit(int k, vector& prices) {
int n = prices.size();
vector>> dp(n,vector(k+1,vector(2,0)));
for(int i = 1;i<=k;i++)dp[0][i][1] = - prices[0];
for(int i = 1;i < n;i++)
for(int j = 1;j<=k;j++){
dp[i][j][0] = max(dp[i-1][j][0],dp[i-1][j][1]+prices[i]);
dp[i][j][1] = max(dp[i-1][j][1],dp[i-1][j-1][0]-prices[i]);
}
return dp[n-1][k][0];
}
}; 3.2 买卖股票的最佳时机1
本题非常契合这个转移图,因为k=1,我们不需要对k进行处理,只需要构建一个二维数组即可:
关键区别
1)转移方程:
dp[i][0] = max(dp[i-1][0],dp[i-1][1] + prices[i]);
dp[i][1] = max(dp[i-1][1], - prices[i]);这里一开始令我很疑惑,为什么第二行是- prices[i] 而不是 dp[ i - 1][0]- prices[i]
看了其他人解释发现,
dp【i】【1】表示,第i天手里不持有股票状态(这里的不持有股票有三种情况,一是从第0天到第i天,一直没买过股票,二是第i天之前的某一天买过股票,我们在第i天卖掉,三是在第i天之前已经有过一次买股票和一次卖股票的操作了所以在第i天是不持有股票的状态),能有的最多的利润
而我们想要的是 从第0天到第i天,一直没买过股票,然后今天进行buy操作,如果直接使用 dp[ i - 1][0]的话,我们并不能区分当前是第几次交易,而本题只允许一次
且第一种情况利润为0,因此我们直接用0替代第一种情况即可
2)初始化:
根据定义即可,这里只需要初始化第0天的一个大小为2的一维数组即可
其他部分不多赘述,完整代码如下:
class Solution {
public:
int maxProfit(vector& prices) {
int n = prices.size();
vector> dp(n,vector(2,0));
dp[0][0] = 0;
dp[0][1] = -prices[0];
for(int i = 1;i < n;i++){
dp[i][0] = max(dp[i-1][0],dp[i-1][1] + prices[i]);
dp[i][1] = max(dp[i-1][1], - prices[i]);
}
return dp[n-1][0];
}
};
3.3 买卖股票的最佳时机2
此题和股票买卖1的差别在于不限制交次数,那么buy的时候就可以使用 dp[ i - 1][0]- prices[i]进行更新,其余相同,代码如下:
class Solution {
public:
int maxProfit(vector& prices) {
int n = prices.size();
vector> dp(n,vector(2,0));
dp[0][0] = 0;
dp[0][1] = -prices[0];
for(int i = 1;i < n;i++){
dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i]);
dp[i][1] = max(dp[i-1][1], dp[i-1][0]- prices[i]);
}
return dp[n-1][0];
}
}; 3.4 股票买卖的最佳时机3
本题就是股票买卖4的阉割版,令k=2即可,代码如下:
class Solution {
public:
int maxProfit(vector& prices) {
int n = prices.size();
int k =2;
vector>> dp(n,vector(k+1,vector(2,0)));
for(int i = 1;i<=k;i++)dp[0][i][1] = - prices[0];
for(int i = 1;i < n;i++)
for(int j = 1;j<=k;j++){
dp[i][j][0] = max(dp[i-1][j][0],dp[i-1][j][1]+prices[i]);
dp[i][j][1] = max(dp[i-1][j][1],dp[i-1][j-1][0]-prices[i]);
}
return dp[n-1][k][0];
}
}; 3.5 最佳买卖股票时机含冷冻期
此题就只多了一个冷冻期条件,我们仔细观察这个条件:
是对buy进行限制,也就是我们要buy的话,需要考虑前一天是否sell过
那么可以这样分情况:
1)昨天sell过
我们只能从两天前开始继承,因此buy部分为dp[i-2][0]- prices[i]
2)昨天没有sell
我们可以从昨天进行继承,但是昨天没有卖过,那么dp[i-2][0] == dp[i-1][0] ,因此,buy部分同样为dp[i-2][0]- prices[i]
这种思想在dp的情况讨论中很常见,有时候我们发现一种写法里面包含了多种情况,我们具体分析后就会发现多半是这多种情况的表达式一样
同时注意根据初始化,此处更新涉及到i-2,因此要初始化前两天
完整代码如下:
class Solution {
public:
int maxProfit(vector& prices) {
int n = prices.size();
vector> dp(n,vector(2,0));
dp[0][0] = 0;
dp[0][1] = -prices[0];
if(n == 1)return 0;
dp[1][0] = max(dp[0][0],dp[0][1] + prices[1]);
dp[1][1] = max(-prices[1],dp[0][1]);
for(int i = 2;i < n;i++){
dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i]);
dp[i][1] = max(dp[i-1][1], dp[i-2][0]- prices[i]);
}
return dp[n-1][0];
}
}; 3.6 股票买卖的最佳时机含手续费
此题的区别在于每次交易都要给手续费,但是其他部分不变,也即是在buy或者sell时多减去一个手续费fee即可
那么应该在sell还是buy时候减呢?
答案是都可以:
在sell时减,那么初始化由于只初始化第0天,没有遇到sell的情况,不减去fee
在buy时减,初始化时就要将第一次交易的fee减去
sell时减去fee的代码如下:
class Solution {
public:
int maxProfit(vector& prices, int fee) {
int n = prices.size();
vector> dp(n,vector(2,0));
dp[0][0] = 0;
dp[0][1] = -prices[0];
for(int i = 1;i < n;i++){
dp[i][0] = max(dp[i-1][0],dp[i-1][1] + prices[i] - fee);
dp[i][1] = max(dp[i-1][1],dp[i-1][0] -prices[i]);
}
return dp[n-1][0];
}
};