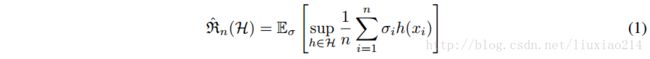论文学习1----理解深度学习需要重新思考泛化Understanding deep learning requires rethinking generalization

——论文地址：Understanding deep learning requires rethinking generalization

---

1、有关新闻

1.1 新闻一：

参考1：机器之心

尽管深度人工神经网络规模庞大，但它们的训练表现和测试表现之间可以表现出非常小的差异。传统的思考是将小的泛化误差要么归结为模型族的特性，要么就认为与训练过程中的正则化技术有关。

通过广泛的系统性实验，我们表明这些传统的方法并不能解释大型神经网络在实践中泛化良好的原因。具体而言，我们的实验表明一个当前最佳的用于图像分类的卷积网络（该网络是使用随机梯度方法训练的）可以轻松拟合训练数据的随机标签。这个现象在质量上不受特定的正则化的影响，而且即使我们将真实图像替换为完全非结构化的随机噪声，这个现象依然会发生。我们通过一个理论构建（theoretical construction）证实了这些实验发现，表明：只要参数的数量超过了数据点的数量（实践中常常如此），那么简单的 2 层深度的神经网络就已经有完美的有限样本表达能力（finite sample expressivity）了。

我们通过与传统模型的比较而对我们的实验发现进行了解释。

1.2 新闻二：

参考2：雷锋网-夏睿

该论文由Chiyuan Zhang（麻省理工学院），Benjamin Recht（加利福尼亚大学伯克利分校），Samy Bengio、Moritz Hardt（谷歌大脑）和Oriol Vinyals（谷歌深度学习）共同完成。

论文摘要

有些成功运作的人工神经网络，尽管体量巨大，但它们在训练和测试性能两个阶段表现出来的结果却只存在微小差异。过去大家认为这种微小误差，要么是由于模型谱系自身的特性，要么是由在训练期间使用的正则化技术所致。

经过大量系统实验，我们展示了这种传统观点是不确切的。具体来说，我们的实验证明了用随机梯度方法训练的、用于图像分类的最先进的卷积网络很容易拟合训练数据的随机标记。这种现象本质上不受显式正则化影响，即使用完全非结构化随机噪声来替换真实图像也是如此。

我们通过一个理论结构证实了实验结果。理论结构表明，只要参数数量超过实际中通常存在的数据点，简单两层深度神经网络（simple depth two neural networks）就能够产生完美的有限样本表达性。通过与传统模型的比较解释了我们的实验结果。

最终评审结果是这样评价的

作者在论文中阐述了深度神经网络拟合随机标签数据的能力，并给出了非常不错的实验结果。调查不仅合理，且有启发和激励意义。作者提出1. 一个理论实例，说明一个具有足够规模参数的简单浅层网络能够产生完美的有限样本表达性；2.一个系统且广泛的实验评估得以支持研究结果和论点。实验评估模型考虑得很周到。

该论文所具有的开创性意义将会在未来几年对许多研究起到启发作用。

1.3 新闻三：

参考3：雷锋网：奕欣

三篇优秀论文中争议最大的莫过于这篇名为《Understanding Deep Learning Requires Rethinking Generalization》（《理解深度学习，需要重新思考泛化问题》）的论文。作者为 Chiyuan Zhang（MIT博士生，师从Tomaso Poggio）、Samy Bengio（谷歌大脑团队，深度学习三巨头 Yoshua Bengio的亲兄弟）、Modiz Hardt（谷歌大脑团队）、Benjamin Racht（加州伯克利大学），Oriol Vinyals（谷歌DeepMind）。从标题到阵容，不得不承认是非常豪华的。不过，观点在 OpenReview 上呈现两极分化，以纽约大学博士生张翔为代表的研究者认为此文被高估，而评审的最终结果却认为它具有重要的学术意义。

回顾论文的内容。成功的神经网络在训练与测试性能之间存在非常小的差异，但传统观点认为这是泛化误差的结果。这篇论文就以「重新思考泛化问题」为主题，通过系统试验，展示传统方法无法解释大规模神经网络在实践中的泛化表现好的原因。而在实验中，研究者证明了用随机梯度训练、用于图像分类的 CNN 很容易拟合随机标签数据，而且本质上并不受显式正则化的影响。

评论：作者在论文中阐述了深度神经网络拟合随机标签数据的能力，并给出了非常不错的实验结果。这个调查不仅全面，也具有启发意义。作者提出了 a) 一个理论实例，说明一个具有足够规模参数的简单浅层网络能够产生完美的有限样本表达性；b) 系统广泛的实验评估得以支持研究结果。这个实验评价是一个具有彻底性的模型。毋庸置疑，这是一项具有颠覆性的工作，将会启发未来数年的许多研究。

MIT 博士生周博磊也认为这篇论文加深了研究者们「对神经网络的理解，也给人们开了个新的视角来看问题」，这个问题在知乎上有所回答。

不过，师从 Yann LeCun 的纽约大学博士生张翔则在 OpenReview 上公开对这篇论文提出了不同意见，认为此文获得 oral 的殊荣对于理论学界并不公平。他也在评论中强调，他的观点与实验室及导师无关，纯粹是阐述他个人的意见。雷锋网 AI 科技评论第一时间联系了张翔，并与他进行了简短的交流。

从张翔的角度来看，他认为这篇论文归根结底可以总结为：在跟输入无关的随机标签下，模型的泛化能力很差。「我的反对意见是，论文实验中采用的与输入无关的随机标签训练神经网络模型，是极端显而易见且没有意义的，这个结果并没有教给研究人员任何新的知识。」

根据论文的介绍，张翔认为这样数据下训练的模型在遇到没有见过的测试输入时也会输出无意义的标签，因此它在随机标签问题下过拟合得很厉害。而论文中还使用哈德玛克复杂度（Rademacher complexity，下称哈氏复杂度）来说明传统机器学习理论会达到复杂度的最大值，得出了需要「重新思考泛化」的结论。

而张翔在 OpenReview 上表达的反对意见，则指出论文中仅靠一种哈氏复杂度的构造方式，就一定要找到这种构造方式下的对立问题，用他的玩笑话来说就是「拿着锤子，看什么都是钉子」。

「在理论方面，随机标签的数据和正常标签的数据完全就是两个不同的问题，这篇文章用前者说明问题，而学术界对后者才有最大的兴趣。同时，这篇论文中对于传统机器学习理论的使用（基于哈氏复杂度）仅仅是其中一种构造方式，如果我们将哈氏复杂度用于优化目标而不是分类错误率上，由于这两个函数的上下界存在性上的不同，我们并不能够得到论文中『复杂度可以达到最大值』的结果。此外，对于随机标签问题和正常标签问题，理论学界的研究已经有所进展，论文中说『需要重新思考泛化』是非常不合适的，对理论界的诸多前辈的研究工作非常不公平。」

1.4 OpenReview评价与知乎评价：

参考4：OpenReview评价

参考5：知乎评价

2、主要内容

摘要

尽管深度人工神经网络规模庞大，但它们的训练表现和测试表现之间可以表现出非常小的差异。传统的思考是将小的泛化误差要么归结为模型族的特性，要么就认为与训练过程中的正则化技术有关。

通过广泛的系统性实验，我们表明这些传统的方法并不能解释大型神经网络在实践中泛化良好的原因。具体而言，我们的实验表明一个当前最佳的用于图像分类的卷积网络（该网络是使用随机梯度方法训练的）可以轻松拟合训练数据的随机标签。这个现象在本质上不受特定的正则化的影响，而且即使我们将真实图像替换为完全非结构化的随机噪声，这个现象依然会发生。我们通过一个理论构建证实了这些实验发现，表明：只要参数的数量超过了数据点的数量（实践中常常如此），那么简单的 2 层深度的神经网络就已经有完美的有限样本表达能力了。

我们通过与传统模型的比较而对我们的实验发现进行了解释。

1、介绍

深度人工神经网络经常有比他们本身训练的样本数量还要多很多的训练模型参数。这些模型之间表现出非常小的泛化误差，例如训练误差和测试误差。同时，这很容易提出一种想法，自然模型架构的泛化能力差。那么然后如何从中区分哪些神经网络泛化的好呢？一个满意的答案不仅帮助神经网络更容易理解，而且使得模型结构设计更有原则，更可靠。

为了回答这个问题，统计学习理论提出了一系列复杂的措施，使其有能力控制泛化误差。这包括VC维，Rademacher complexity（拉德马赫复杂性）和一致稳定性。此外，当参数的数量非常大时，理论证明，一些正则化的方法需要确保泛化误差很小。正则化可能就是early stopping的一种含蓄表示。

—插播—解释上面三个名词：参考博客：1，2。—

1.1 我们的贡献

在这项工作中，我们通过展示传统方法不能有效区分不同神经网络之间的本质上不同的泛化表现，将关于泛化的传统观点问题化。

随机取样测试 我们的方法论的核心就是，我们已知的从无参数统计中随机取样测试的变体。在第一组实验中，我们在数据的复制样本上，用随机标签替换了其正确的标签，然后用来训练几个标准架构。我们主要的发现可以总结为：

         ***深度神经网络可以很好的拟合随机标签***

更准确的来说，当在一个真实数据的完全随机标签上训练时，神经网络实现了0训练误差。当然，在训练标签和测试标签没有任何联系的情况下，测试误差几乎和这种随机训练一样。换句话说，通过独立地将标签随机化，我们可以强制一个模型的泛化误差大大地上升，而不改变这个模型，包括其大小，超参数，或者是优化器。我们针对，在CIFAR10和ImageNet分类标准上训练的，几个不同的标准架构，建立了这个事实。而从统计学的角度来看，这一观察结果有着深远意义：

• 1、神经网络的有效能力足以记住整个数据集。

• 2、即使是对随机标签的优化也很容易。事实上，与在真实标签上的训练相比，训练时间的提高仅仅是因为一个小的常数因子。

• 3、随机化标签是一个单独的数据转换，学习问题的其他属性并没有改变。

在第一组实验上扩展，我们用完全随机的像素替代了真实图像，并且观察到卷积神经网络继续拟合数据而且训练误差为0。这展示了不管他们的结构，卷积神经网络仍然可以拟合噪音。我们进一步改变了随机取样的数量，在无噪音和完全是噪音的例子是平滑的插入。这导致了一系列的中间学习问题：标签上仍然有一定程度的信号。我们观察到，随着我们提高噪音级别，泛化误差也在平稳的退化。这解释了神经网络有能力捕捉数据中剩余的信号，与此同时并用蛮力拟合噪音。

明确正则化的作用 如果一个模型结构本身不是一个足够的正则化器，那它可以拿来证明显式正则化是如何起到帮助作用的。我们展示了正则化的显式形式，例如，weight decay，dropout和data augmentation，这没有充分的解释神经网络的泛化误差。换句话说：

   ***显式正则化可以提高泛化性能，但是这既不必要对于其自身也不足够来控制泛化误差。***

与传统的凸的经验风险最小化相比，其显式正则化将明显解排除在外是必要的，我们发现正则化在深度学习中扮演了一个不同的角色。这看起来似乎是，更多地参数协调，经常可以帮助提高模型最终的测试误差，但是所有正则化的缺少并不一定意味着差的泛化误差。正如Krizhevsky等人提出的一样，L2正则化（weight decay）有时甚至能对最优化有所帮助，这说明在深度学习中，其性质了解的不够充分。

有限样本的表达能力 我们用理论构建补足了我们的经验观测值，这个理论构建表明，一般的大型神经网络可以表达训练数据的任何标签。更正式的，我们建立了一个两层RelU网络，带有p=2n+d个参数，在d维空间中，它可以表达任意大小n的样本的任意标签。Livni等人先前的构建实现了一个类似的结果，但是带有更多的参数，也就是O(dn)。尽管我们的2层深度网络不可避免的有比较大的宽度，但是我们也提出了一个k层深度的网络，其每一层都只有O(n/k)个参数。

尽管先前的表达结果集中于，什么样的函数神经网络可以表示整个域，我们现在转而关注对于有限样本，神经网络的表示能力。与现在深度空间上的函数分离相比，我们的结果展示出，即使是有些线性大小的2层深度网络，也早已可以表示训练数据的任意标签。

隐式正则化的作用 尽管像dropout和weight-decay的显式正则化对泛化可能并不是必不可少的，但这是确定的，不是所有拟合训练数据的模型都可以泛化的很好。事实上，在神经网络中，我们通常是将我们的模型作为随机梯度下降的输出。对于线性模型，随机梯度下降总是收敛到一个小标准的解。因此，算法本身隐式地正则化了这个结果。事实上，我们展示出，在小的数据集上，不需要正则化，高斯核方法就可以泛化的很好。尽管这不能解释为什么某个结构比其他结构泛化的更好，这也说明了，更多地调查对于正确的理解使用随机梯度下降训练的模型继承了那些性质是必要的。

1.2 相关工作

就梯度下降所采用的步数而言，Hardt等人给出了，用随机梯度下降训练的模型关于泛化误差的一个上限。他们的分析利用了一致稳定性的概念。正如我们在这项工作中所指出的，学习算法的一致稳定性独立于训练数据的标签，因此，这个概念不足以区分在正确标签（小的泛化误差）上训练的模型和在随机标签（高泛化误差）上训练的模型。这也强调了为什么Hardt等人的分析对于非凸的最优化问题比较悲观，只允许少数测试通过数据。我们的结果表明，即使是以经验为主的训练神经网络对于很多通过数据的测试也不是一致稳定的。因此，一个较弱的稳定性概念对于沿着这个方向获取进一步的发展是必要的。

从一般的逼近原理到多层感知器，对于神经网络的表征能力还有大量的工作要做。所有的这些结果，在群体层面上，可以描述出，神经网络族可以表示整个域上的那些数字函数。因此，我们学习对于大小为n的有限样本的神经网络的表征能力。这引出了一个非常简单的证明，即使是O(n)大小的两层感知器也有表征一般有限样本的能力。

Bartlett证明，使用sigmoid激励函数的多层感知器，就每个节点使用L1标准的权重，其宽松的shatter的维度的上限。这个重要的结果给出了对于神经网络的泛化上限，它独立于网络的大小。然而，对于RelU网络，L1标准则不再适用。这也导致了一个问题，对于大型神经网络，是否有对限制泛化误差有不同形式的能力控制。这个问题由Neyshabur等人在一个发人深省的工作中提出。一个对矩阵因子分解的类比阐述了隐式正则化的重要性。

2、神经网络的有效能力

我们的目标是了解前馈神经网络的有效模型容量。为了这个目标，受无参数随机测试启发，我们选择了一个方法。特定的，我们选定一个候选结构，同时在真实数据和数据的复制（其真实的标签被替换成随机的标签）上训练它。在第二种情形下，实例和类之间不再有任何关系，因此学习是不可能的。直觉暗示，这种不可能在训练过程中可以很明显的表现出来，例如，通过训练不会大幅缩减或者缩减的很慢的。令我们吃惊的是，对于多层标准结构来说，训练过程中的几个特性很大程度上不受标签变化的影响。这提出了一个概念上的挑战。无论我们是以什么样的理由开始，期待一个小的泛化误差，这都不再适应于随机标签的情况。

为了进一步深入了解这一现象，我们使用不同级别的随机采样进行试验，在无标签噪音和完全损坏标签之间探索联系集。我们也试了对于不同输入（而不是标签）的随机采样，也得出了相同的结论。

这个实验在两个图像分类数据集上运行，CIFAR10数据集和ImageNet ILSVRC 2012数据集。我们在ImageNet测试了Inception V3结构，和一个更小的Inception，在CIFAR10测试了Alexnet和MLPs。可以在附录A部分获取关于实验装置的更多细节。

2.1 拟合随机的标签和像素

我们通过对标签和输入进行一下的修改来进行我们的实验：

• 真实标签：没有做修改的原始数据集。

• 部分损坏的标签：独立于可能性p，每一个图像的标签由一个统一的随机类进行损坏。

• 随机标签：所有的标签都由随机标签来替换。

• 打乱的像素：对像素选择一个随机的置换，接着这个置换应用于训练和测试集上所有的图像上。

• 随机像素：每一个图像的随机置换不同且独立。

• 高斯：对每一个图像，使用高斯分布（与原始图像数据集有匹配的均值和方差）来产生像素。

惊人地，未改变超参数的随机梯度下降可以优化权重来完美地拟合随机标签，即使这些随机标签完全破坏了标签和图像之间的关系。通过洗牌图像像素，我们进一步地打破了图像的结构，甚至完全从高斯分布随机取样像素点，但是我们测试的网络依旧有能力拟合。

图1：在CIFAR10拟合随机标签和随机像素。（a）展示出，不同实验设置的训练损失随着训练步数的衰减。（b）展示出，不同标签损坏率的相对收敛时间。（c）展示出，不同损坏程度的标签下的测试误差（因为训练误差是0，所以这也是泛化误差）。

图 1a 展示了，在CIFAR10数据集上，Inception模型在不同设置下的学习曲线。我们预期目标函数会花更长的时间在随机标签上进行衰减，因为最初时每一个训练样本的标签分配都是毫不相关的。因此，大的预测误差通过后向传播，对于参数更新，获取大的梯度。然而，因为随机标签在每个时期都是固定且一致的，但是在训练集经过多次训练后网络就开始拟合。我们发现，对于拟合随机标签，以下的观察很有趣：a）我们不需要改变学习速率表；b）一旦拟合开始，它将收敛的很快；c）它收敛到完美地拟合训练集。当然，也要注意，“随机像素”和“高斯”比“随机标签”开始收敛的快。这可能是因为，对于随机像素，相对于原始的属于同一类别的自然图像，现在的输入更为分散，因此，对于任意标签分配也更容易建立网络。

在CIFAR10数据集上，Alexnet和MLPs在训练集上都收敛到了0损失。表1中的阴影行展示了精确的数字和实验装置。我们也在ImageNet数据集上测试了随机标签。正如附录中表2最后三行展示的那样，尽管他没有达到完美的100%的准确度，95.20%对于1000个类别的100万随机标签来说也是很惊人的。注意，当从真实标签转换为随机标签时，我们并没有做任何超参数的改动。很有可能，如果做一些超参数的调整，在随机标签上的完美准确度就可以实现。即使是在使用显式正则化的时候，这个网络也能达到前90%的准确度。

部分损坏的标签 在CIFAR10数据集上，我们进一步观察了在不同级别损坏程度（从0（无损坏）到1（完全随机标签））的标签下训练的神经网络的表现行为。在所有情况下，这个网络完美地拟合了损坏的训练集。在图1b中展示了，随着标签噪音级别的提高，收敛时间的减慢。图1c描述了收敛后的测试误差。在噪音级别方法1中，泛化误差收敛到了90%，也就是在CIFAR10数据集上随机猜测的性能。

2.2 影响

从我们的随机化实验出发，我们讨论了，我们的发现是如何对关于泛化原因的传统方法提出了挑战。

Rademacher复杂度和VC维 Rademacher复杂度通常用来测量假设类别的灵活的复杂性的。在数据集{x1,x2,,,,xn}上的假设类H的经验Rademacher复杂度通常被定义为：

其中，，且独立同分布于均匀随机变量。这种定义与我们的随机测试很相似。特别的，衡量了H对于拟合随机的±1二分类标签的能力。如果我们考虑多分类问题，对于已有的相同实验的观察，可以直接考虑相关的二分类问题。尽管我们的随机测试表明，很多神经网络可以完美地拟合有着随机标签的训练集，我们还是期待，对于相对应的模型类别H，。当然，在Rademacher复杂度中，这是一个不重要的上限，在现实的设置中不会产生有用的泛化边界。类似的推理也应用于VC维中，其对宽松的shatter维度的连续推论对于我们进一步限制这个网络并没有用。但是Bartlett证明了，就网络权值上的L1标准限制范围而言，一个在那宽松shatter维度上的限制，这个限制并没有应用于我们这里所考虑的RelU网络。这个结果由Neyshabur等人推广到其他标准，但即使是这样，似乎也不能解释我们所观察到的泛化行为。

一致稳定性 从假设类的复杂性度量走出来，我们考虑在训练时所使用的算法的性质。通常是从一些稳定性的概念开始做的，例如一致稳定性。算法A的一致稳定性衡量了，对于替换一个单一的例子算法的敏感度。然而，它仅仅是算法的一个属性，并没有考虑到数据的细节和标签的分布。定义一个关于稳定性更弱的概念是可能的。最弱的稳定性度量是直接等价于限制泛化误差，并将数据考虑在内。然而，有效利用这些较弱的稳定性的概念还是很困难的。

表1：不同模型在CIFAR10数据集上的训练和测试准确度（比分比）。在使用data augmentation和weight decay与否的性能上做了比较。也包括了拟合随机标签的结果。

3、正则化的作用

我们随机化测试中的大多数是在关闭显式正则化的情况下执行的。在理论和实践上正则化是一个标准工具，来减缓当参数比数据点还多的这种体制的过拟合。基本的观点是，尽管原始假设太大了以至于泛化的很好，但是正则化帮助将学习限制在一个有着可管理的复杂性的假设空间的子集上。通过添加一个显式正则化，也就是通过惩罚最优解的标准，可能解的Rademacher复杂性显著地减少。

正如我们看到的那样，在深度学习上，显式正则化似乎发挥不同的作用。正如附录中表2的最低行表示的那样，即使是使用dropout和weight decay，InceptionV3仍然可以拟合随机训练集，即使不完美，也做得非常好。尽管没有明确的展示出，在CIFAR10数据集上，使用weight decay的情况下，Inception和MLPs仍然可以完美地拟合随机训练集。然而，使用weight decay的AlexNet在随机标签上没有收敛。为了调查在深度学习上正则化的作用，我们明确的比较了有无正则化的深度网络学习的表现行为。

我们并没有对所有引进于深度学习的各种正则化做全调查，我们简单地拿了几个常用的网络结构，当关闭了正则化之后，比较了他们的行为。主要覆盖了以下正则化：

• Data augmentation：通过特定域的转换增大训练数据集。对于图像数据，通常使用的转换包括随机剪切，随机扰乱亮度、饱和度、色度和对比度。

• Weight decay：等同于在权值上的L2正则化；也等同与把权值严格限制在一个欧式球内，半径由weight decay的数量决定。

• Dropout：在给定dropout可能性下，将一层中的每个元素的输出随机屏蔽。在我们的实验中，只有在ImageNet数据集上，ImageNet使用了dropout。

表1展示了在CIFAR10数据集上，Inception，Alexnet和MLPs的结果。使用了data
augmentation和weight decay。尽管正则化技术帮助提高泛化性能，但是即使所有的正则化都关闭，所有的模型依然可以泛化的很好。

附录的表2展示了，在ImageNet数据集上相同的实验。当我们关闭了所有的正则化后，18%的top-1准确度是观察到的。特别的，在没有正则化后，top-1的准确度是59.80%，而随机猜测只实现了0.1%的top-1准确度。更为显著地，当使用data-augmentation，其他正则化关闭的时候，Inception可以实现72.95的top-1准确度。事实上，看起来，使用已知对称性增大数据的能力比只是简单调整weight decay，或者阻止低的训练误差，更为有力得多。

Inception在没有正则化的情况下实现了80.38%的top-5准确度，而ILSVRC 2012获奖者报告的数量是83.6%。因此，既然正则化重要，简单改变模型的结构可以得到更大的收获。这很难说，在深度网络的泛化能力中，正则化是作为一个基本的相变。

3.1 隐式正则化

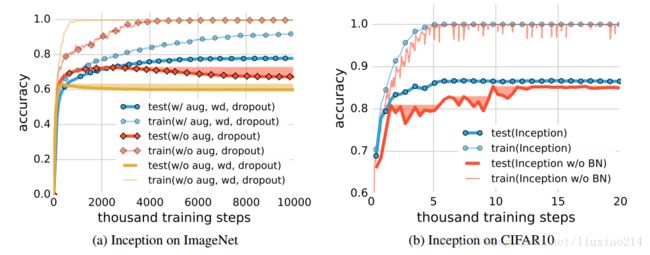
图2：隐式正则化在泛化性能上的效果。aug是data augmentation，wd是weight decay，BN是weight decay。隐形区域是累积测试最好的准确度，作为early stopping潜在性能获得的一个指示器。（a）当没有其他正则化的时候，early stopping可以潜在的提高泛化。（b）early stopping在CIFAR10数据集上未必是有用的，但是batch normalization使得训练过程稳定并且改善了泛化。

我们展示的early stopping在一些凸的学习问题上隐式地正则化了。在附录的表2中，我们展示出，括号中显示的是在训练过程中最好的测试准确度。这使得确认，early stopping可以潜在的提高泛化性能。图2a展示了ImageNet数据集上的训练和测试的准确度。阴影区域表示累积最好的测试准确度，作为early stopping潜在性能获得的一个参考。然而，在CIFAR10数据集上，我们并没有观察到early stopping任何潜在的好处。

Batch normalization是一个操作者，使得每个小批量的层相应标准化。它被广发地应用于很多现代神经网络架构中，例如Inception和Residual Networks。尽管对正则化没有准确的设计，batch normalization通常用来提高泛化性能。Inception结构使用了大量的batch normalization层。为了测试batch normalization的影响，我们创建了一个“Inception w/o BatchNorm”结构，跟图3中的Inception相同，除了所有的batch normalization层都去除了。图2b比较了在CIFAR10数据集上，所有的显式正则化关闭，Inception两个变体的学习曲线。正规化操作者帮助学习动态稳定，但是在泛化性能上的影响只有3~4%。在表1“Inception w/o BatchNorm”部分中，列出了确切的准确度。

总结来说，我们同时在显式和隐式正则化上的观察一致表明，适当的调整正则化，可以提高泛化性能。然而，这不见得正则化就是泛化的一个基本原因，而且在所有正则化移除之后，网络依然表现的很好。

4、有限样本的表达能力

大部分的努力都在描述神经网络的表示能力上，例如，e.g,Cybenko(1989);Mhaskar (1993); Delalleau & Bengio (2011); Mhaskar & Poggio (2016); Eldan & Shamir (2016);Telgarsky (2016); Cohen & Shashua (2016)。几乎所有的这些结果都是“群体层面”上的，这表示出，整个域的函数可不可以由一个有着相同数量参数的神经网络的确定类别表示。例如，众所周知，在群体水平上，深度k比深度k-1更为有力。

我们认为，在实践中，更为相关的是神经网络对于有限的，大小为n的数据集的表示能力。使用一致收敛理论，将群体水平的结果转换为有限样本的结果是可能的。然而，这种一致收敛边界要求是相同的大小，以使得在输入维度上是多项式大的，在网络深度上是指数的，这在实际中是一个不切实际的要求。

我们转而直接分析神经网络对于有限样本的表示能力，注意，这极大地简化了图像。特别地，只要一个网络中参数的数量p比n大，即使是简单的2层神经网络也可以表示输入样本的所有函数。我们认为神经网络C可以表示在d维空间中，样本大小为n的所有函数，

定理1.存在使用RelU激励函数的两层神经网络，其2n+d个权重可以表示在d维空间中样本大小为n的任意函数。

证明在附录的C部分给出，我们也将实现在深度k下的宽度O（n/k）。我们认为这只是一个简单的练习，在我们的构建中，给予系数向量的权重限制。引理1给了矩阵A最小的特征值的一个限制，这可以用于给解决方法w的权值的一个合理的限制。

5、隐式正则化：线性模型的呼吁

尽管由于很多原因深度神经网络依然保持神秘，我们注意到，在这一部分，这也很不容易理解线性模型中泛化的来源。事实上，对线性模型中简单的例子进行上诉，以找出类似的观点，来帮助我们更好的理解神经网络，这是有用的。

假设我们收集了n个不同的数据点，其中xi是d维空间的特征向量，yi是标签，使用loss来表示非负的损失函数，，考虑经验风险最优化的问题（empirical risk minimization，ERM），

如果d>n，我们可以拟合任意标签。但是，在如此丰富的模型类别，且没有明确的正则化下，泛化是有可能的吗？

用X来表示nxd的数据矩阵，其中第i行是。如果X的秩为n，则方程式Xw=y会有有限个解，而不管右边是什么。我们可以通过简单的解这个线性方程系统，就可以在ERM问题上找到一个全局最小值。

但是所有的全局最小值都会泛化的一样好吗？是否有方法来确认有一个全局最小值泛化的很好，而其他都不好吗？理解最小值的质量的一个常用的方法就是，在这个解上损失函数的曲率。但是在线性的例子中，所有最优解的曲率是相同的。要明白这个，注意在这个例子中，yi是一个标量，

当y是向量值时，可以发现类似这样的方程。特别的，Hessian并不是一个用来选择w的函数。此外，Hessian在所有的全局最优解上都是退化的。

如果曲率不能区分全局最优，那么什么能呢？一个有前景的方向是考虑主力算法，随机梯度下降，并且检查随机梯度下降收敛到哪个解。因为随机梯度下降使用来更新，其中是步长大小，是预测误差损失。如果w0=0，对于一些系数α来说，我们肯定会有一个解，其形式为。因为，如果我们运行随机梯度下降，我们会得到存在于这个数据点之中。如果我们完美地对标签进行了篡改，我们将有。强制执行这两个身份，这可以简化为单个方程：

其有独一的解。注意，该方程仅仅取决于数据点xi之间的点积。我们因此推导出“kernel trick”—尽管是用一个迂回的方式。

因此我们可以完美地拟合任意标签集，通过在数据形成Gram矩阵（又名内核矩阵），并且解决了线性系统。这是一个nxn的线性系统，无论n小于10万时，这可以在标准的工作站上解决，就像CIFAR10和MNIST这样小基准的测试。

相当出人意料的是，对于凸模型来说，拟合训练标签的效果非常好。在未加预处理的MNIST数据集上，通过简单的解决方程（3），我们可以实现测试误差1.2%，注意这并不简单，因为内核矩阵需要30GB的存储内存。尽管如此，在一个有着24芯片，256G的RAM，和一个惯例的线性代数程序包的工作站上，这个系统还是可以在3分钟之内解决，首先应用Gabor小波转换的数据，接着解决方程（3），在MNIST上的误差可以降到0.6%。惊奇的是，添加正则化后并没有提高任一模型的性能。

对于CIFAR10数据集也是类似的结果。简单地对像素采用高斯核，没有使用正则化，实现了46%的测试误差。通过带有32000个随机滤波器的随机卷积神经网络进行预处理，测试误差降到了17%。进一步添加L2正则化，将这一误差数字降到了15%。注意，这并没有使用任何的data augmentation。

请注意，该内核解决方法在隐式正则化方面具有吸引人的解释。简单的代数揭露了这等价于Xw=y的最小二值解。也就是说，完全拟合数据的所有模型中，随机梯度下降经常以最小的标准收敛到解决方法上。这很容易构造出不会发生泛化的Xw=y的解：例如，一个可以拟合高斯核数据，并将中心放在随机点上。另一个例子强制数据在测试数据集上拟合随机标签。在这两种情形下，解的范数要比最小解的范数大得多。

不幸的是，最小范数的概念对于泛化性能并没有预测性。例如，回到MNIST数据集例子，没有预处理的最小范数解的L2范数大约为220。小波预处理后，范数涨到了390。尽管因为因素2，测试误差下降。但是最小范数的直觉对于新算法的设计，可以提供一些指导，这只是泛化故事中非常小的一部分。

6、结论

在这项工作上，对于定义和理解机器学习模型有效能力的概念，我们提出了一个简单的实验框架。我们构建的这个实验强调了，几个成功的神经网络结构的有效能力是足够大的，以至于可以shatter所有的训练数据。因此，这些模型在原则上已经足以记忆训练数据。这种情况对于统计学理论提出了一个概念上的挑战，传统衡量方法，模型的复杂性难以解释大型人工神经网络的泛化能力。我们认为，在这些大型网络如此简单的情况下，我们尚未发现精确、正式的衡量方法。我们的实验得出的另一个结论是，即使得到的模型不能泛化，在经验上，优化仍然是简单的。这表明，为什么经验上优化如此简单的原因与泛化的真正原因不同。

3、个人感受