一维差分，二维差分（详解＋例题）

一、一维差分

1.1、解释：

        设数列an，记an为数列bn的前n项和

        原数组：a[1],a[2],a[3],a[4]..................a[n];

   构造一个数组b：b[1],b[2],b[3],b[4].................b[i];

使得a[i] = b[1] + b[2] + b[3] + ........ + b[i];

也就是说，a数组是b数组的前缀和数组，反过来我们把b数组，叫做a数组的差分数组。换句话说，每一个a[i]都是b数组中从头开始的区间和。

1.2、样例：

a[0] = 0
b[1] = a[1];
b[2] = a[2] - a[1];
b[3] = a[3] - a[2];
...           .....
b[i] = a[i] - a[i-1];

1.3、作用： 

• 让一个序列中某个区间内的所有值均加上或减去一个常数C。

• 可以将对a数组任意区间的同一操作从O(n)优化到O(1)。

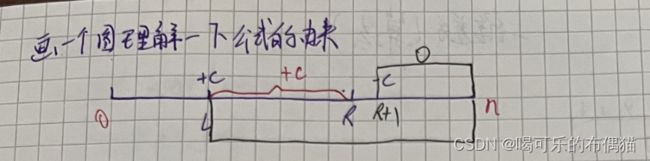
我们只需要让差分数组b中，区间[l,r]中的所有值都加上常数C，
b[l] += c;
b[r+1] -= c;

解析：

a[l] = b[1]+b[2]+...+b[l-1]+b[l]; 

......                                 .......;

a[r] =  b[1]+b[2]+...b[l]+...+b[r]; 

a[r+1] = b[1]+b[2]+...b[l]+...+b[r]+b[r+1];

我们只向让[l,r]之间的和加C不想让后面r+1之后的也加C，所以我们让b[r+1] -= c;

1.4、核心代码：

•   对a数组区间[l,r]同时加上c的操作可转化为：

• void insert(int l, int r, int c)
  {
      b[l] += c;
      b[r+1] -= c;
  }
  //求前缀和
  for(int i = 1; i <= n; i++)
  {
      b[i] += b[i-1];
      printf("%d ",b[i]);
  }

  1.5、例题：此题来源于Acwing

AC代码如下：

#include

using namespace std;

const int N = 100010;
int a[N],b[N];
int n,m;

//构造差分数组
void insert(int l,int r,int c)
{
    b[l] = b[l] + c;
    b[r+1] = b[r+1] - c;
}

int main()
{
    scanf("%d %d", &n, &m);
    for(int i=1;i<=n;i++) scanf("%d ", &a[i]);;
    //默认b数组是0，开始构造差分数组
    /*举个例子：
    例如：样例中的a数组 1 2 2 1 2 1
    1,1,a[1]传入，b[1] = b[1] + a[1];
    b[2] = b[2] - a[1];
    这是一次传入，第二次：b[2] = b[2] + a[2] ---->这里b[2] = -a[1] ---->正好满足差分概念
    b[3] = b[3] - a[2]
    */
    for(int i=1;i<=n;i++) insert(i,i,a[i]);
    
    while (m -- )
    {
        int l,r,c;
        scanf("%d %d %d ",&l,&r,&c);
        insert(l,r,c);
    }
    
    for(int i=1;i<=n;i++)
    {
        //复原 原数组，求前缀和
        b[i] = b[i] + b[i-1];
    }
    
    for(int i=1;i<=n;i++) printf("%d ",b[i]);
    return 0;
}

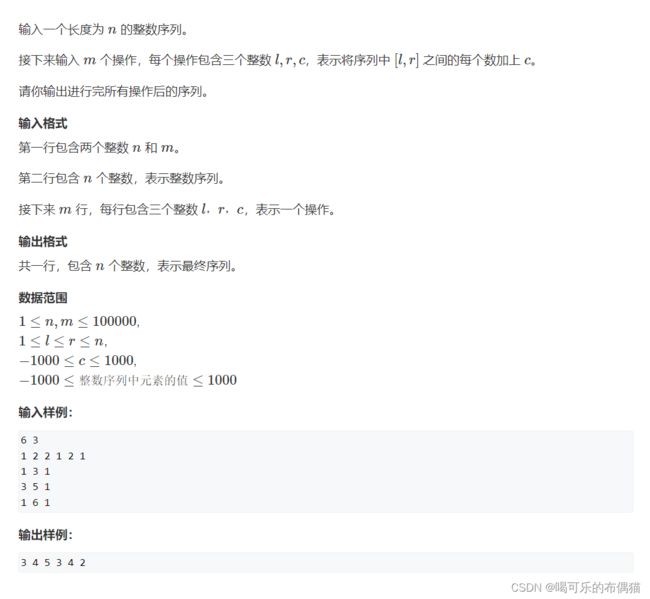
 题目样例解析：

• 样例：

  比如 ： 1 2 2 1 2 1（原数组） 下标从1开始

  1 1 0 -1 1 -1（差分数组）构造之后的

• 我们通过上面两种方法进行构造，第二种方法，我们可以这么理解，假定a数组和b数组最开始为0，对于每一个a数组

  和b数组最开始为0，对于每一个a[i] 相当于插入一个数，进行计算，具体例子代码注释上有。

---

二、二维差分 

 1.1、图解：

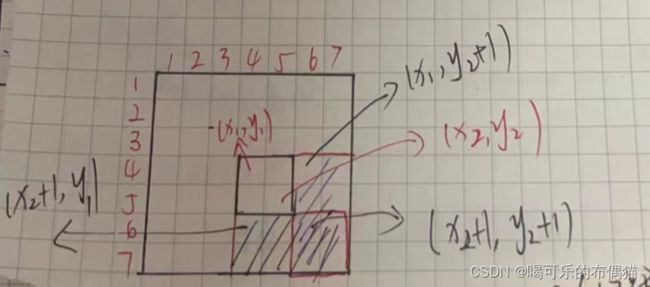
如图上图，我们想要求小的黑色方块+c后的结果，首先，根据公式b[x1] [y1] += c ,改变的从 (x1,y1)这个点到右下角的所有值都加C

我们想要是只让小黑方块里加C即可，其他位置不变，那么我们就需要类比一维差分让画虚线的部分减c，下面是黑阴影面积，右面是紫色阴影面积，所以我们要让（紫色阴影面积部分）b [x1] [y2+1] += c, 和 （黑色阴影面积）b [x2+1] [y1] += c, 然后我们可以发现重叠的部分多加了一次C，所以我们再让重叠部分减去C即可，（重叠部分）b [x2+1] [y2+1] += c,用来抵消，这样正好其他的地方都不会发生变化。

由此，我们可以推出公式：

    b[x1][y1] += c;
    b[x2+1][y1] -= c;
    b[x1][y2+1] -= c;
    b[x2+1][y2+1] += c;

1.2、例题：此题来源于ACwing

AC代码如下： 

#include

using namespace std;

const int N = 1010;
int b[N][N],a[N][N];

//构造差分数组
void insert(int x1,int y1,int x2,int y2,int c)
{
    b[x1][y1] += c;
    b[x1][y2+1] -= c;
    b[x2+1][y1] -= c;
    b[x2+1][y2+1] += c;
}

int main()
{
    int n,m,q;
    scanf("%d %d %d", &n, &m,&q);
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)
        {
            scanf("%d", &a[i][j]);
        }
    }
    //假定a数组和b数组都是0，去构造差分数组b
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)
        {
            insert(i,j,i,j,a[i][j]);
        }
    }
    
    while (q -- )
    {
        int x1,y1,x2,y2,c;
        scanf("%d %d %d %d %d",&x1,&y1,&x2,&y2,&c);
        insert(x1,y1,x2,y2,c);
    }
    //求加完之后的原数组（前缀和方法 ）
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)
        {
            b[i][j] = b[i-1][j] + b[i][j-1] - b[i-1][j-1] + b[i][j];
        }
    }
    //输出
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)
        {
            printf("%d ",b[i][j]);
        }
        puts("");
    }
    return 0;
}

关于构造b数组代码解释：

for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)
        {
            insert(i,j,i,j,a[i][j]);
        }
    }

 我们可以先设想a数组为空，那么b数组一开始也为空，但实际上数组a并不为空，因为我们每一次让b数组以（i，j）为左上角到以（i，j）为右下角面积内元素（其实就是一个小方块面积）插入c=a[i][j]。

---

以上综合大佬博客和个人理解所整理，如果有错的地方，欢迎指出~