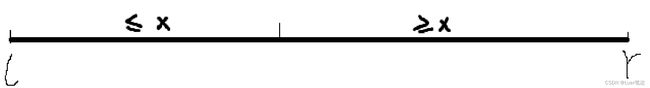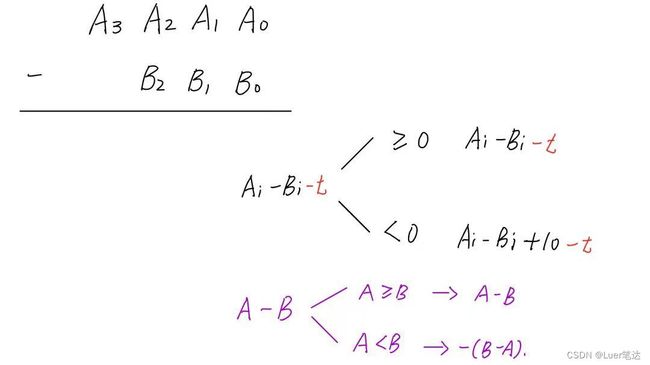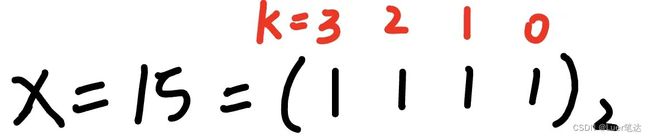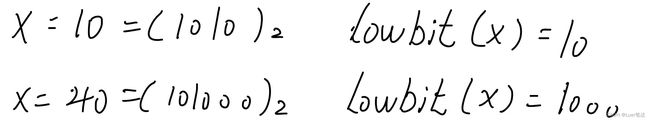01.基础算法
一、快速排序(是基于分治法的)
1、算法思想
①确定这组数中的分界点x:
确定方式:取左边界q[l]、取中间值q[ (l+r) / 2 ]、取右边界限q[r]、随机取一个数
②调整区间(难点):
通过x的值将区间一分为二划分为两部分(这两部分长度不一定相等),
使得左半部分中的所有元素值≤x,
右半部分中的所有元素值≥x。
【注意】分界点上的数不一定是x,x可能在很奇怪的位置。
③递归排序左段和右段。
左段排好序,右段排好序,左右拼接则整体排好序
2、代码实现
#include
using namespace std;
const int N = 1e6 + 10;
int n;
int q[N];
void quick_sort(int q[], int l, int r)
{
if (l >= r) return;
int x = q[(l+r)/2], i = l - 1, j = r + 1;//Acwing中把q[l]改为q[(l+r)/2]可提交成功!
while (i < j)
{
do i++; while (q[i] < x);
do j--; while (q[j] > x);
if (i < j) swap(q[i], q[j]);
}
quick_sort(q, l, j);
quick_sort(q, j + 1, r);
}
int main()
{
cin >> n;
for (int i = 0; i < n; i++) cin >> q[i];
quick_sort(q, 0, n - 1);
for (int i = 0; i < n; i++) cout << q[i] << " ";
return 0;
} 输入样例:
5
3 1 2 4 5输出样例:
1 2 3 4 53、练习
1)算法思想
2)代码实现
#include
using namespace std;
const int N = 100010;
int n, k;
int a[N];
int quick_select(int a[], int l, int r, int k)
{
if (l >= r)
{
return a[l];
}
int x = a[(l + r) / 2], i = l - 1, j = r + 1;
while (i < j)
{
do i++; while (a[i] < x);
do j--; while (a[j] > x);
if (i < j)
{
swap(a[i], a[j]);
}
}
int sl = j - l + 1;
if (k <= sl)
{
return quick_select(a, l, j, k);
}
return quick_select(a, j + 1, r, k - sl);
}
int main()
{
cin >> n >> k;
for (int i = 0; i < n; i++)
{
cin >> a[i];
}
int res = quick_select(a, 0, n - 1, k);
cout << res << endl;
return 0;
}
二、归并排序(是基于分治法的)
1、算法思想
①确定分界点:mid = ( l+r ) / 2;
②根据分界点将区间分为left部分[l, mid] 和 right部分[mid + 1, r],递归排序left部分和right部分;
③归并:合二为一;
2、代码实现
#include
using namespace std;
const int N = 1000010;
int n;
int q[N], tmp[N];
void merge_sort(int q[], int l, int r)
{
if (l >= r) return;
int mid = (l + r) / 2;
merge_sort(q, l, mid), merge_sort(q, mid + 1, r);
int k = 0, i = l, j = mid + 1;
while (i <= mid && j <= r)
if (q[i] <= q[j]) tmp[k++] = q[i++];
else tmp[k++] = q[j++];
while (i <= mid) tmp[k++] = q[i++];
while (j <= r) tmp[k++] = q[j++];
for (i = l, j = 0; i <= r; i++, j++) q[i] = tmp[j];
}
int main()
{
cin >> n;
for (int i = 0; i < n; i++) cin >> q[i];
merge_sort(q, 0, n - 1);
for (int i = 0; i < n; i++) cout << q[i] << " ";
return 0;
} 输入样例:
5
3 1 2 4 5
输出样例:
1 2 3 4 53、练习
1)算法思想:
2)代码实现:
#include
using namespace std;
const int N = 1e5 + 10;
int q[N], tmp[N];
int n;
long long merge_sort(int q[], int l, int r)
{
if (l >= r)
{
return 0;
}
int mid = (l + r) / 2;
long long res = merge_sort(q, l, mid) + merge_sort(q, mid + 1, r);
int k = 0, i = l, j = mid + 1;
while (i <= mid && j <= r)
{
if (q[i] <= q[j])
{
tmp[k++] = q[i++];
}
else
{
tmp[k++] = q[j++];
res += mid - i + 1;
}
}
while (i <= mid)
{
tmp[k++] = q[i++];
}
while (j <= r)
{
tmp[k++] = q[j++];
}
for (int i = l, j = 0; i <= r; i++, j++)
{
q[i] = tmp[j];
}
return res;
}
int main()
{
cin >> n;
for (int i = 0; i < n; i++)
{
cin >> q[i];
}
cout << merge_sort(q, 0, n - 1) << endl;
return 0;
} 三、二分法(本质上属于边界问题)
1、整数二分
典型的应用:一组有序数中查某个元素k的起始位置和终止位置,元素k在这组有序数中可能出现多次,返回结果就是第一次出现时的位置和最后一次出现时的位置,也就是元素k的起始边界和终止边界,若元素k只出现一次,则起始位置和终止位置相同。我们课本上的二分法只适用于一个元素的情况。
1)算法思想
设q为一组有序数,mid为中间位置下标,l和r分别为首尾位置的下标,x为待查找的关键字。
①先找x的左边界(即x第一次出现的地方)
while(l < r){
mid = (l+r) / 2;
if(x <= q[mid]) 在[l, mid]区间查找x,更新r = mid;
else 在[mid+1, r]区间查找x,更新l = mid+1;
}
当l==r时循环结束,l的值为x的左边界下标
②后找x的右边界(即x最后一次出现的地方)
while(l < r){
mid = (l+r+1) / 2; //多加1防止死循环
if(x >= q[mid]) 在 [mid, r] 区间查找x,更新l = mid;
else 在 [l, mid-1] 区间查找x,更新r = mid-1;
}
当l==r时循环结束,l的值为x的右边界下标
2)代码实现
int l = 0, r = n - 1;
while (l < r)
{
int mid = (l + r) / 2;
if (x <= q[mid]) r = mid;
else l = mid + 1;
}
//上面的while循环以两种情况结束,
//以l==r结束表示查找成功,x==a[l], 会执行if下面的else语句块
//以l>r结束表示查找失败,x!=a[l], 会执行if语句块输出-1 -1
if (q[l] != x) cout << "-1 -1" << endl;//找不到返回-1 -1
else
{
cout << l << ' ';
int l = 0, r = n - 1;
while (l < r)
{
int mid = (l + r + 1) / 2;
if (x >= q[mid]) l = mid;
else r = mid - 1;
}
cout << l << endl;
}2、浮点数二分
开平方“根号x”的例子。
#include
using namespace std;
int main()
{
double x;
cin >> x;
double l = 0, r = x, mid;
while (r - l > 1e-6)
{
mid = (l + r) / 2;
if (x <= mid * mid)
{
r = mid;
}
else
{
l = mid;
}
}
cout << l << endl;
return 0;
} 3、练习
四、高精度
1、存储方式
以数字“123456789”为例,把该数从个位到高位依次存储在以下数组中
2、加法
1)算法思想
2)代码实现
#include
#include
using namespace std;
const int N = 1e6 + 10;
vector add(vector &A, vector &B)
{
vector C;
int t = 0; // t表示第i位的进位,个位时由于没有任何进位,故初值为0
// 第一轮的循环表示两数的个位相加 + 进位(0)
// 第二轮的循环表示两数的十位相加 + 进位(0 or 1)
// 第三轮的循环表示两数的百位相加 + 进位(0 or 1)
// ...
for (int i = 0; i < A.size() || i < B.size(); i++) // 循环条件是两数中有一个数的第i位存在,就可以计算了
{
if (i < A.size()) // 数A的第i位存在,把数A的第i位用t加一下
{
t += A[i];
}
if (i < B.size()) // 数B的第i位存在,把数B的第i位用t加一下
{
t += B[i];
}
C.push_back(t % 10); // 此时,, Ci = (Ai + Bi) % 10 + (Ai + Bi) / 10
t /= 10;
}
// 这里主要是为了处理A数中最高位为9时最后进一的情况
if (t)
{
C.push_back(1);
}
return C;
}
int main()
{
string a, b;
vector A, B;
cin >> a >> b;
for (int i = a.size() - 1; i >= 0; i--)
{
A.push_back(a[i] - '0'); // '某数字字符'的ASCII码 - '0'的ASCII码 = 某数字
}
for (int i = b.size() - 1; i >= 0; i--)
{
B.push_back(b[i] - '0'); // '某数字字符'的ASCII码 - '0'的ASCII码 = 某数字
}
vector C = add(A, B);
for (int i = C.size() - 1; i >= 0; i--)
{
cout << C[i]; //输出时候从高位到个位,对应到数组中就是从最后一个数到第一个数依次输出
}
return 0;
} 3、减法
1)算法思想
2)代码实现
#include
#include
using namespace std;
// 判断是否有 A >= B
bool cmp(vector &A, vector &B)
{
if (A.size() != B.size())
{
return A.size() > B.size();
}
for (int i = A.size() - 1; i >= 0; i--)
{
if (A[i] != B[i])
{
return A[i] > B[i];
}
}
return true;
}
// C = A - B
vector sub(vector &A, vector &B)
{
vector C;
int t = 0;
for (int i = 0; i < A.size(); i++)
{
t = A[i] - t;
if (i < B.size())
{
t -= B[i];
}
C.push_back((t + 10) % 10);
if (t < 0)
{
t = 1;
}
else
{
t = 0;
}
}
while (C.size() > 1 && C.back() == 0)
{
C.pop_back();
// 将高位部分多余的0删除,最后要的结果是7而不是007
// 127
//- 120
//-----------
// 007
}
return C;
}
int main()
{
string a, b;
vector A, B;
cin >> a >> b;
for (int i = a.size() - 1; i >= 0; i--)
{
A.push_back(a[i] - '0');
}
for (int i = b.size() - 1; i >= 0; i--)
{
B.push_back(b[i] - '0');
}
if (cmp(A, B))
{
vector C = sub(A, B);
for (int i = C.size() - 1; i >= 0; i--)
{
cout << C[i];
}
}
else
{
vector C = sub(B, A);
cout << "-";
for (int i = C.size() - 1; i >= 0; i--)
{
cout << C[i];
}
}
return 0;
} 4、乘法
1)算法思想
2)代码实现
#include
#include
using namespace std;
vector mul(vector& A, int b)
{
vector C;
int t = 0;
for (int i = 0; i < A.size(); i++)
{
if (i < A.size())
{
t += A[i] * b;
}
C.push_back(t % 10);
t /= 10;
}
if(t)
{
C.push_back(t);
}
return C;
}
int main()
{
string a;
int b;
cin >> a >> b;
vector A;
for (int i = a.size() - 1; i >= 0; i--)
{
A.push_back(a[i] - '0');
}
vector C = mul(A, b);
for (int i = C.size() - 1; i >= 0; i--)
{
cout << C[i];
}
return 0;
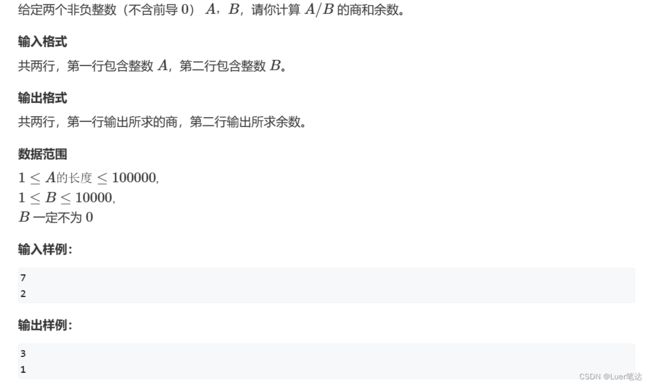
} 5、除法
1)算法思想
2)代码实现
#include
#include
#include
using namespace std;
// A / b, 商是C,余数是r
vector div(vector& A, int b, int &r) // r是引用
{
vector C; // 商
r = 0;
for (int i = A.size() - 1; i >= 0; i--)
{
r = r * 10 + A[i];
C.push_back(r / b);
r %= b;
}
reverse(C.begin(), C.end());
while (C.size() > 1 && C.back() == 0)
{
C.pop_back();
}
}
int main()
{
string a;
int b;
cin >> a >> b;
vector A;
for (int i = a.size() - 1; i >= 0; i--)
{
A.push_back(a[i] - '0');
}
int r;
vector C = div(A, b, r);
for (int i = C.size() - 1; i >= 0; i--)
{
cout << C[i];
}
cout << endl << r << endl;
return 0;
} 五、前缀和
1、一维前缀和
1)算法思想
2)代码实现
#include
using namespace std;
const int N = 100010;
int n, m;
int a[N], s[N];
int main()
{
cin >> n >> m;
for (int i = 1; i <= n; i++)
{
cin >> a[i];
}
for (int i = 1; i <= n; i++)
{
s[i] = s[i - 1] + a[i]; // 前缀和的初始化
}
while (m--)
{
int l, r;
cin >> l >> r;
cout << s[r] - s[l - 1] << endl; // 区间和的计算
}
} 2、二维前缀和
1)算法思想
2)代码实现
#include
using namespace std;
const int N = 1010;
int n, m, q;
int a[N][N], s[N][N];
int main()
{
cin >> n >> m >> q;
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= m; j++)
{
cin >> a[i][j];
}
}
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= m; j++)
{
s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + a[i][j];
}
}
while (q--)
{
int x1, y1, x2, y2;
cin >> x1 >> y1 >> x2 >> y2;
cout << s[x2][y2] - s[x2][y1 - 1] - s[x1 - 1][y2] + s[x1 - 1][y1 - 1] << endl;
}
return 0;
} 六、差分
1、一维差分
1)算法思想
2)代码实现
#include
using namespace std;
const int N = 1000010;
int n, m;
int a[N], b[N];
void insert(int l, int r, int c)
{
b[l] += c;
b[r + 1] -= c;
}
int main()
{
cin >> n >> m;
for (int i = 1; i <= n; i++)
{
cin >> a[i];
}
for (int i = 1; i <= n; i++)
{
insert(i, i, a[i]);
}
while (m--)
{
int l, r, c;
cin >> l >> r >> c;
insert(l, r, c);
}
for (int i = 1; i <= n; i++)
{
b[i] += b[i - 1];
}
for (int i = 1; i <= n; i++)
{
cout << b[i] << " ";
}
cout << endl;
return 0;
} 2、二维差分
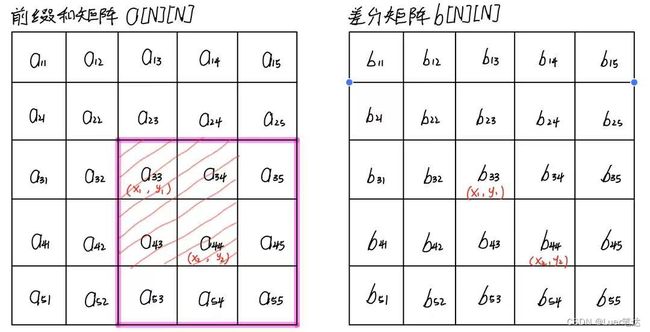
1)算法思想
给定前缀和矩阵a[N][N],构造差分矩阵b[N][N],使得a[N][N]是b[N][N]的前缀和。
差分核心操作:给以(x1,y1)为左上角,(x2,y2)为右下角的子矩阵中的所有元素a[i][j]加上C。
对于差分矩阵b的影响:
b[x1][y1] += C;
b[x1][y2+1] -= C;
b[x2+1][y1] -= C;
b[x2+1][y2+1] += C;
2)代码实现
#include
using namespace std;
const int N = 1010;
int n, m, q;
int a[N][N], b[N][N];
void insert(int x1, int y1, int x2, int y2, int c)
{
b[x1][y1] += c;
b[x2 + 1][y1] -= c;
b[x1][y2 + 1] -= c;
b[x2 + 1][y2 + 1] += c;
}
int main()
{
cin >> n >> m >> q;
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= m; j++)
{
cin >> a[i][j];
}
}
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= m; j++)
{
insert(i, j, i, j, a[i][j]);
}
}
while (q--)
{
int x1, y1, x2, y2, c;
cin >> x1 >> y1 >> x2 >> y2 >> c;
insert(x1, y1, x2, y2, c);
}
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= m; j++)
{
b[i][j] += b[i - 1][j] + b[i][j - 1] - b[i - 1][j - 1];
}
}
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= m; j++)
{
cout << b[i][j] << " ";
}
cout << endl;
}
return 0;
} 七、双指针算法
1、双指针算法的种类
第一类:两个指针分别指向两个序列(如归并排序)
第二类:两个指针共同指向一个序列(如快速排序)
2、双指针算法通用模板:
for(int i = 0, j = 0; i < n; i++)
{
while(j < i && check(i, j))
{
j++;
}
// 每道题目的具体逻辑
}3、双指针算法最核心的作用:
先看两重循环的暴力做法:
for(int i = 0; i < n; i++)
{
for(int j = 0; j < i; j++)
{
// 每道题目的具体逻辑
}
}这个两重循环的暴力做法的时间复杂度是O(n^2),而双指针算法的核心作用就是把它优化到O(n),因为双指针算法的两个指针的移动次数不超过2n。
4、最简单的双指针算法的例子
题目:输入一个字符串,字符串中每个单词用空格隔开,把里面的每个单词输出。
#include
#include
using namespace std;
int main()
{
char str[1000];
gets(str);
int n = strlen(str);
for (int i = 0; i < n; i++)
{
int j = i;
while (j < n && str[j] != ' ')
{
j++;
}
//这道题目的具体逻辑
for (int k = i; k < j; k++)
{
cout << str[k];
cout << endl;
i = j;
}
}
return 0;
} 5、双指针算法的解题方法
第一步:先思考用暴力法如何解
第二步:将暴力法转换成我们的模板去做。
例题:
for(int i = 0; i < n; i++)
{
for(int j = 0; j <= i; j++)
{
if(check(j, i))
{
res = max(res, i - j + 1);
}
}
}双指针算法:
for(int i = 0; i < n; i++)
{
while(j <= i && check(j, i))
{
j++;
}
res = max(res, i - j + 1);
}#include
using namespace std;
const int N = 100010;
int n;
int a[N], s[N];
int main()
{
cin >> n;
for (int i = 0; i < n; i++)
{
cin >> a[i];
}
int res = 0;
for (int i = 0, j = 0; i < n; i++)
{
s[a[i]]++;
while (s[a[i]] > 1)
{
s[a[j]]--;
j++;
}
res = max(res, i - j + 1);
}
cout << res << endl;
return 0;
} 八、位运算
1、位运算的一些操作
1)找出x的二进制数中第k位数字是几
例:
算法思想:
①先把第k位数字移到最后一位:x >> k;
②看个位是几,(x >> k) & 1;
2)lowbit(x):返回x的最后一位1
例:
算法思想:x&(-x)
分析思想:
该操作的一个应用:统计x的二进制中1的个数
#include
using namespace std;
int lowbit(int x)
{
return x & (-x);
}
int main()
{
int n;
cin >> n;
while (n--)
{
int x;
cin >> x;
int res = 0;
while (x)
{
x -= lowbit(x);
res++;
}
cout << res << " ";
}
return 0;
}