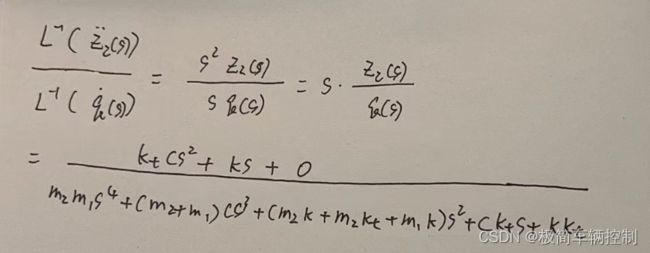汽车悬架二自由度模型搭建与仿真

1、随机路面建模

1）、随机路面时域公式

随机路面的时域模型推导如下:

 

   我们要的是时域的路面模型，即每一时刻下，路面的高度是多少，单从上面这个公式和这个表，还没法建模，上面的拟合公式只是个参考，意思是:我们的生成的随机路面功率谱只要跟它差不多就可以，至于用什么方法生成随机路面，国标则没规定。一般用白噪声法比较多，推导过程如下所示。

 

 

 

2）、随机路面建模及仿真

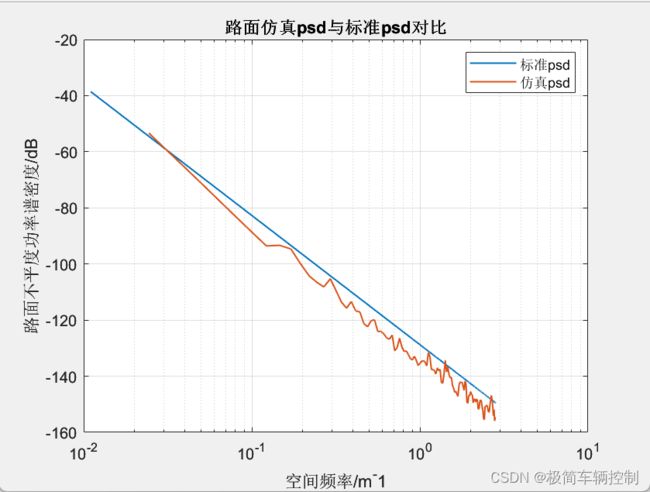
由公式3.18，便可以在simulink中将模型搭建出来，并绘制功率谱密度曲线，与参考功率谱密度曲线对比。simulink模型如下图所示(脚本及模型见文末链接):

在脚本中运行模型，并记录仿真数据，并绘制仿真对比结果。

 结果如下:

 

 仿真得到的功率谱密度曲线与标准路面功率谱密度曲线相近，因此可以用于悬架仿真，作为路面输入。

2、双质量2自由度模型

1）、传递函数推导

 上图所示是一个车身与车轮两个自由度的振动系统，它的运动方程如下:

 假设初始状态都为0，对两个式子进行拉式变换，得到Z2/q的传递函数，:

 上图是簧上位移到路面位移的传递函数，如果想得到簧上加速度到路面高度变化率的传递函数，也很容易得到，稍微变形就可得到，如下所示:

2）、传递函数曲线 

一般常拿簧上加速度作为舒适性评判的指标，所以我们这里分析便拿簧上加速度与路面高度变化率的传递函数来进行分析。参数设置如下(完整脚本见文末链接)

簧上加速度与路面高度变化率之间的幅频特性曲线如下所示。取图上两个尖峰点，分别为车身和车轮的偏频附近的点。直观的理解:如果路面高度变化率是频率1.5hz，幅值为1m/s的正弦波输入，则簧上加速度输出数值是输入数值的26.5倍。我们可以在matlab脚本里实验一下。

实际仿真也恰好如此。

 3）、偏频:

车身偏频: 假设车轮m1不动，只有车身质量m2的单自由度无阻尼自由振动，其固有频率(也就是上图第一个共振点)是由弹簧刚度和簧上质量m2决定的，满足   单位是rad/s。

车轮偏频：假设车身m2不动，只有车轮质量m1的单自由度无阻尼自由振动，其固有频率(上图第二个共振点)是由弹簧刚度、轮胎刚度和车轮质量共同决定的，满足 

将我们设置的悬架参数代入到这两个公式，可以算得车身共振频率 f0=1.59hz，车轮共振频率点ft=15.1hz。

一般情况下，f0和ft在一辆车设计过程中就已经确定，我们所讲的半主动悬架控制无法改变这两个点，但是通过一些算法，可以降低共振点的幅值，使得舒适性提高。

4）、不同阻尼下的效果

我们设置5组不同阻尼，分别为1700，3200，4700，6200，7700，看下传递特性会怎样:

 从图中可以看到，在车身共振频率f0附近，大阻尼更能抑制车身共振，但是在车身共振频率与车轮共振频率之间的频率段，大阻尼的效果却不如小阻尼的好。在车轮共振频率点后面的频率，是小阻尼效果最好。传统单一阻尼的曲线只能在这好跟坏之间折中。

从这里我们就能发现半主动悬架阻尼控制的目标: 在车身共振频率附近达到大阻尼的效果，在车身共振频率点后面的频率段，都达到小阻尼的效果。

3、与路面结合时域分析

1）、搭建simulink的悬架二自由度模型

根据这两个方程搭建模型:

有一个技巧，先把积分模块放上去，然后求解最高阶导数便可以，搭完效果如下(完整模型文件见文末链接。)

 输入即来源于第一部分提到的随机路面模型。

同样设置C=[1700,3200,4700,6200,7700]，5组参数，运行脚本和模型，查看结果，这里我们只关心簧上加速度这个信号。

2)、时域结果

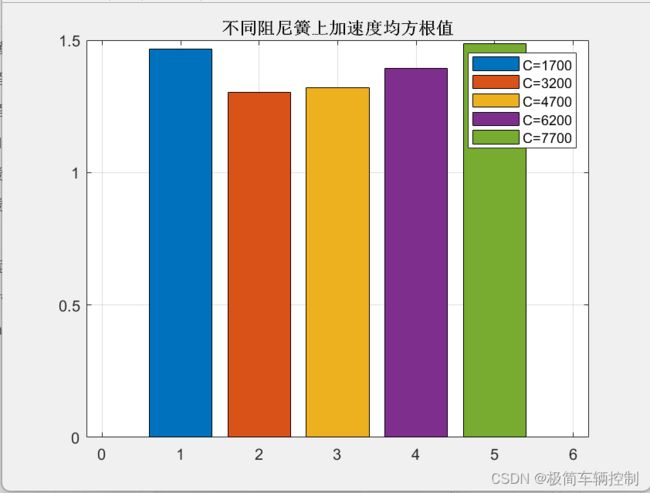
 不能很明显看出差别。看下均方根值:

从图上可以看到，中间值阻尼的效果较好。

3)、频域结果

经过，随机路面----simulink悬架模型----簧上加速度---傅里叶变换---响应频谱图，注意体会下与上一部分传递函数频率曲线的差别。这边是从结果的角度，上一部分是从物理方程本身传递过程的角度。

 在1.5hz左右，高阻尼效果好，在车身共振频率到车轮共振频率之间则是低阻尼效果好，在车轮共振频率附近，各阻尼效果差不多。结果与第二部分从传递函数角度出发分析出来的结果一致。

4、脚本和模型

包含，点击以下链接就可看到:

 1、simulink随机路面模型，路面参数，功率谱密度脚本；
 2、悬架二自由度模型传递函数，不同阻尼分析脚本;
 3、悬架二自由度simulink模型，时域，频域，傅里叶变换工具脚本
原创、资料整理不易，各位看官老爷如有需要，就当请我喝个饮料了吧。